Several centuries before Christ, Euclid’s «Elements» stablished the fundaments of the known Geometry. Those fundaments remained unquestioned until the XIX century.
It stablished 5 simple and self evident postulates, from which Euclid deduced and remonstrated logically all the Geometry. But fifth postulate created many difficulties to mathematicians through the History. Many of them thought, from the beginning, that the fifth postulate did not seem a simple and self-evident postulate but a theorem which should require to be demonstrated.
In that sense there were many unsuccessful attempts through the subsequent centuries trying to demonstrate the fifth postulate like if it were a theorem, basing on the 4 first Euclidean simple postulates. even it has been speculated that Euclid himself could have attempted to demonstrate the fifth postule, and as he was unable he decided to include it as a last postulate that must be assumed.
At the beginning of the XIX century, the Russian mathematician Nicolai Lobachevsky thought that the Euclid’s fifth postulate could not be demonstrate through the postulates 1-4 and he started a different approach, to try to demonstrate that the fifth postulate was wrong instead of demonstrating it was correct.
The fifth postulate states that “If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles”.
This postulate has been known as the «Parallels» postulate because it forms the basis for the Euclid’s theory of parallels.
From it, the so-called “Playfair’s axiom» can be deduce stating that “there is at most one line that can be drawn parallel to another given one through an external point”.

As Euclid did not determine thoroughly the definition of straight line, Lobachevsky thought that a curved line following a straight direction could be considered as a straight line preserving the coherency with all the Euclid’s postulates and the subsequent geometry except with his fifth postulate. For example in a sphere, the lines on the curved space are curved but follow a straight direction; In a section of the sphere the curved straight line, the circle, is on a flat plane.
Lobachevsky demonstrated the disability of the Parallels postulate when it comes to working with curved spaces and developed his new geometry in an axiomatic way and by using equations but without having a visually referential model for that kind of geometry. He was able to draw visually some elements of the new geometry but without a complete representation model. His development was so abstract that himself called the new geometry as «imaginary geometry», imaginary as opposite to real life geometry although we thought it was the way which was Nature works in.
The new geometry that does not follow the fifth Euclidean postulate is known as non-Euclidean or Hyperbolic geometry. It has been developed during the last two centuries and have had an essential role in the developing of the modern physics. After Lobachevsky many different models or representations of the non-Ecucliean geometry appeared, as the Riemann Sphere or the named «pseudo sphere» where the parallels converge on the poles, and some others.

It has been told that Lobachevsky’s new geometry represented a true Copernican revolution in mathematics. As always happens in the History of science, almost at the same time than Lobachevsky, other mathematicians like Gauss and Bolyai, were also working on non-Euclidean geometries.
Lobachevsky considered his geometry as a interaction between spaces and he spoke about the concurrence of two dimensions. But it seems the Lobachevsky’s geometry that our mathematicians currently consider is the non-Ecclidean geometry passed through the filter of ulterior developments like the Riemann geometry and so on.
I created these diagrams that I think could be a representation of the Lobachevsky’s imaginary geometry:


On the above diagram, the third parallel is a complex line formed with a part of the parallels 1 and 2. It is a consequence of the interaction of the curved spaces that take place by the mutual intersection of the space of the two spheres.
The Euclid’s postulates do not determine that one straight line could not be formed by the union or interaction of two pre existent lines. We can build a straight line by unifying two points or by unifying or mixing two pre-existent lines.
Euclid stablished a definition of «parallels» as “straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction”.
We can think that circles are curved straight lines produced indefinitely around the sphere but, are the Lobachevsky parallels on the same plane with respect to the first line?
Having a first line, the new created parallels can converge or intersect between them but they can not converge or intersect with the first line. But are the Lobachevsky parallels on the same plane? I mean, is a straight curved line on a curved or plane space on the same plane than a straight non-curved line? And even more, in the Pythagorean theorem, are the sides and the areas of the squares a^2 and b^2 on the same plane than the sides and the area of the square c^2?
What is a Euclidean plane? i think this concept was not thoroughly determined enough by Euclid because of the lack of comprehension of irrationality. I have already mentioned this idea on previous posts on this blog. I think the circle and its circumference, and the square build on the Hypothenuse of any square, are complex areas formed by the concurrency of a rational and an irrational plane.
When we draw the coordinates XY on a flat space we establish our spatial referential coordinates related to a referential segment of metric related to our referential unity of measure; 1, 1 thumb, 1 step, 1 elbow, whatever 1. We can rotate in a free way those coordinates if we rotate at the same time the whole plane on the space. But If we want to keep the location of our XY coordinates as a fixed reference, and we draw a Z coordinate, we need to be aware that we have created a new plane on the same space. The plane of the XY coordinates is our referential «rational» plane, and the plane of the Z coordinate is our referential «irrational» plane. We can not work on the irrational plane thinking it is the rational one because we will be trying to compare directly to kind of referential magnitudes, the rational and the irrational one. The irrational magnitude is incommensurable with respect to the rational one and that is why we get infinite decimals.
By drawing Z we are not creating a new independent coordinate, we are displacing spatially our initial referential XY plane and the effect, when conserving our spatial XY references, is the same than expending the space we are working on (when displacing Y toward Z) or contracting the space (when displacing Z toward Y).
By displacing Y toward Z we are modifying the accorded length (the unity) our originary referential segment to measure distances on a quadratic XY plane and we are creating a different originary referential magnitude to measure distances, the irrational one.
The c^2 area is equivalent to a^2 and b^2 because the length of the 8 sides of a^2 and b^2, their external symmetry, is equivalent to the length of the two hypothenuses of c^2, its inner symmetry, and the length 4 hypothenuses of a^2 and b^2, their internal symmetry, are equivalent to length of the 4 sides of the square c^2, its external symmetry. But a^ and b^2 are not equal to c^2 because they have and carry different kind symmetries inside and outside.

When it comes to comparing the perimeter and the diameter of the circumference we get infinite decimals on Pi because we are comparing directly the rational and the irrational planes and magnitudes.

Inside of the circle, the square of area 2 which touches with its corners the circle, carry a referential symmetry is incommensurable with respect to the symmetry represented on the square of are 4, outside the circle, which touches with its sides the circle.
The different kind of referential metrics or «gauges» using the Hermann Weyl’s terminology, appear clearly if we divide the square 1 into 4 squares of 0,25, the square 2 into 4 squares of 0,50, and the square 4 in to 4 squares of area 1. Then we trace a central point inside of those squares and measure through any diagonal the distance between the center of the circumference and the center of those squares. The squares 0,25, 1 and 4 follow the same interval that cab be repeated the needed times; but the squares 0,50 and 2 follow another disproportionate segment.

[For measuring distances, we use a referential segment which represent our referential metric with the value 1. We did not measure how many points are inside of that referential segment, we agreed to make the abstraction of considering that distance have the value 1. But it is not a totally pure abstraction because in that segment there is a concrete center which divide it in to two equal parts. We have created a perfect symmetry based on the center of our referential segment.
We can create a segment of value 2 with two segments of value 1, placed at the left an right side of a center of symmetry. We have created a new number, the number 2, perfectly coherent with our referential unity. But if we want to combine the segments 1 and 2, we have a problem. We can not set the center of the mirror symmetry between the segments 1 and 2, it will be always a larger side. But we can create a new number, the number 3, based on the referential segment 1. We can set one segment 1 on the middle of a left and a right segments 1. We have created a new referential segment based on the unity. That’s the way which create prime numbers in. Numbers are not purely abstract entities, they represent symmetry.
We can build a referential square 1 on our referential segment 1, and we determine in an abstract way, that the space inside of that square has the value 1. We also have created, being aware or not, a specific center of symmetry in that referential square. But when we trace the hypothenuse inside of it, we get a segment that is not related to our referential symmetry. And here the disproportion can not be saved with the unity because the disproportion has appeared inside of the referential unity himself, the square of area 1 based on the segment of length 1 based on the quantity number 1.]
In this sense I think the non-Euclidean geometries, as they work with curved lines, are building their parallels by using two different planes related to different kind of referential metrics, the rational and the irrational ones. And that violates the Euclidean definition of parallel which is related to a unique plane. In that sense, Non-euclidean geometries are not contrary to the fifth postulate but do not follow the Euclidean definitions.
In the case of the sphere with curved lines converging at its poles the plane section of sphere is displaced toward up or down to draw the next parallel and it also implies to introduce another plane on the space.
I think non-Euclidean geometries are working with different planes – the rational and the irrational one – on static spaces, or with several planes on periodically variable – expanding and contracting spaces which also implies to work with the temporary «dimension».
A suggestive idea could be consider as equivalent to parallel lines the two kind of originary disproportionate magnitude that are not directly comparable, the rational and the irrational ones; We can not measure one metric in terms of the another one, they are independent, they do not converge; the infinite decimals represent their mutual incommensurability, if we try to compare them, we always get a new decimal. But I think infinite decimals are not possible in a limited segment when it comes to measuring linear distances because at a point, periodically, the two kind of periodical intervals will converge, what will represent that the two parallel lines, the rational and the irrational one, cannot be infinitely parallel.
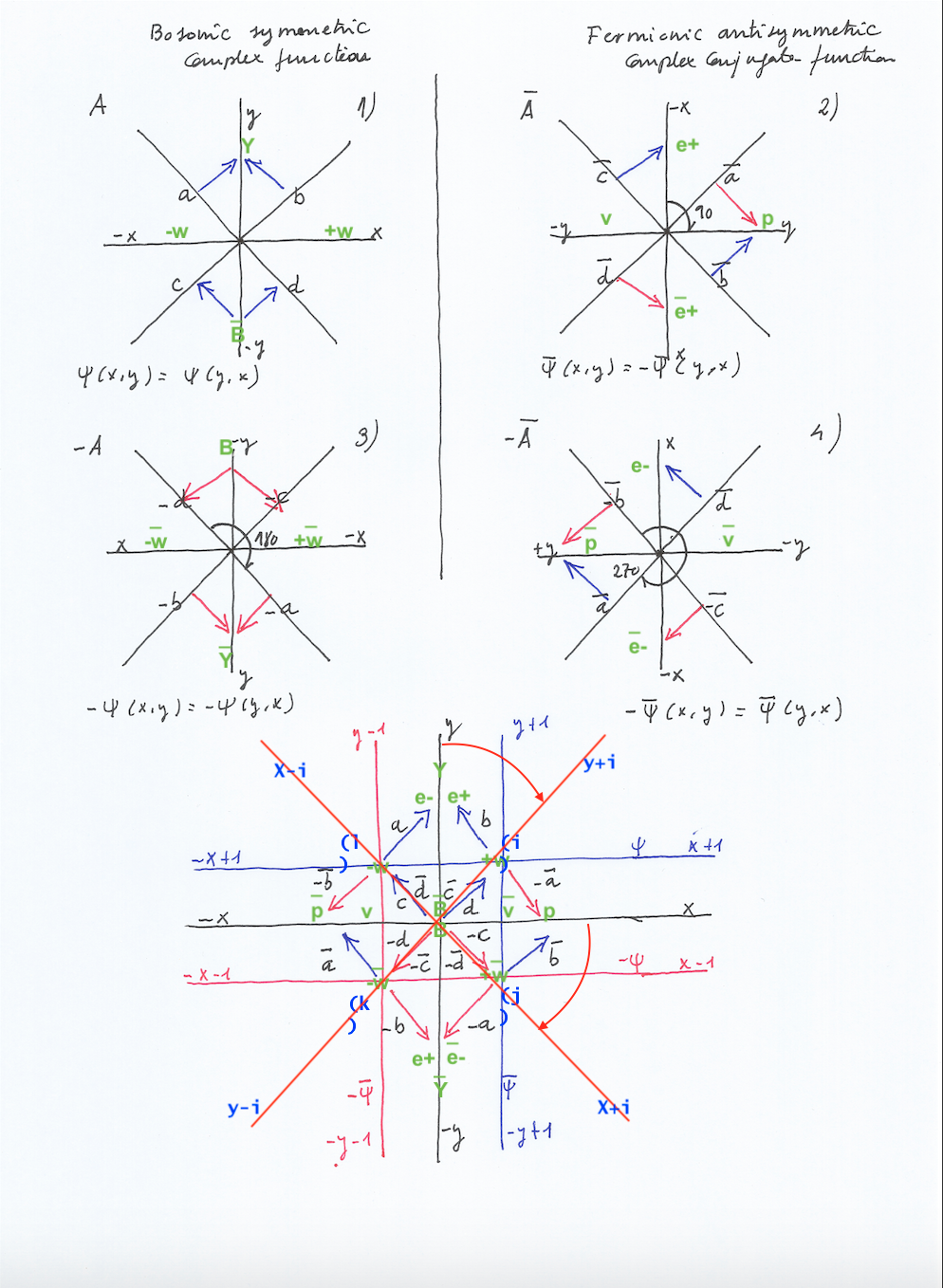
On the picture below i’ve drawn the rational and irrational metric intervals or referential gauges using two different colours, red and blue. You can see there are 7 blue intervals with 8 blue points and 5 red intervals with 6 points. I’m considering the first and last points – the centers of the circumferences – as complex zeros formed at the same time by blue and red points.
Following the diagonal we can see:
Zero blue an red points
1 blue point (blue interval 1)
1 red point (red interval 1)
2 blue point (blue interval 2)
2 red point (red interval 2)
3 blue point (blue interval 3)
XXXXXX (no red point)
4 blue point (blue interval 4)
3 red point (red interval 3)
5 blue point (blue interval 5)
4 red point ( red interval 4)
6 blue point (blue interval 6)
XXXXXX (no red point)
Zero blue and red points where the blue 7th interval and the red 6th interval converge at their respective end.
I think the intervals comprehended inside of the two rows marked with XXXX are what is known in musical terms as the “tritone”. There, the periodical alternation between the two kind of intervals is altered and it is perceived by our senses as something unexpectedly inharmonic.
The zero points, at the center of the circumferences, would represent the so-called non-trivial or relevant zeroes when it comes to determining the periodicity on the appearence of prime numbers following the Riemann’s Z function.

In any case, coming back to the fifth postulate. I think the Euclidean fifth postulate is self-evident and does not requiere further demonstrations when interpreting it literally. I think the parallels to what the fifth postulate is related are the shown in the picture below:

Euclid was specifically speaking about the internal angles – the angles that are inside of the space created by the two parallels that intersect the first horizontal line. If those angles are less than 180 degrees then those parallels will converge on the side of the first horizontal line where the internal angles are less than 180 degrees, and will diverge on the side of the fist horizontal line where the internal angles are higher than 180 degrees. Does it requiere any other demonstration?
I think the so-called “Playfair’s axiome» is a linguistic misinterpretation of the self-evident fifth Euclidean postulate.
So I think the simple meaning of the fifth postulate is that if the angles that are inside of the space created by two lines that intersect to another existent line are smaller than 180 degrees those two lines won’t be parallel between them converging on the side of the first line where those angles are placed and diverging on its other side.
Euclid did not speak in any case about how many parallel can be traced through a point external to an existent line. That was not the aim of the fifth postulate that is speaking about the angles that are not right, being coherent with the sequence of the postulate fourth that speaks about the right angles.
The 4º postulate is about to two equal angles that are right and so sum 180 degrees; the 5º postulate is related to two different and so non-right angles that also sum 180 degrees.
I think Euclide included the 5º as a postulate because of its simplicity and self-evidedence and because it is related to the angles that are not right which is the logical and congruent step after speaking about the angles that are right on the fourth postulate.
The Proposition 27 starts that : «If a straight line that meets two straight lines makes the alternate angles equal, then the two straight lines are parallel».
What is an alternate angle here? In my opinion Euclid considered different elements when it comes to speaking about parallels: An existent line that divides the space in two sides; the notion of internal and external spaces existing inside or outside of the space created by the two parallels; and the idea of alternate angles: following the sequence on the above picture, from right to left: external angle 1, internal angle 1, external angle 2, internal angle 2, the alternate angles are: First, the external angle 1 and the internal angle 2; Second, the internal angle 1 and the external angle 2.
But in the proposition 27 and its demonstration he did not follow the same perspective than in the axiom 5º. Because in the proposition 27 he uses the angles placed on the two sides of the straight line instead of considering only – like in the fifth postulate does – the interior angles of a same side of the straight line.

This is a page of the book «Le problème mathématique de l’espace. Un quête de l’intelligible» by Luciano Boi, speaking about the 27 proposition and the 5º postulate, and the author concludes saying that «il est facile de voir que le raisonnement précédent n’as pas besoin d’admettre le 5º postulate. Celui-ci n’intervient en effect qu’au paragraph 29.»
So, his conclusion is that the 27º proposition is totally independent of the 5º postulate, it has no need to admit the 5º postulate; and that the 5º postulate is only related to the 29º proposition. I think the proposition 27 is not independent at all of the 5º postulate, it shows the parallels considering the two sides of the line while the 5º postulate consideres only one side of the line what implies a different perspective of the same reality.
But the 27º proposition shows that the wording of text of 5º postulate is incomplete because the 5º postulate only mentions the case when the interior angles of the same side of the line are less than 180 degrees but it does not explicitly mention the case when the interior angles of the same side of the line are higher than 180 degrees; the different dimensions, less or higher, will depend on the side from and towards which we displace the two parallel lines to cause their convergence or divergence:

The two lines are only parallels when the two interior angles of the same of the line side are equal 180 degrees.
In this sense the fifth postulate should state that: “If a straight line falling on two straight lines makes the interior angles on the same side less or higher than two right angles, the two straight lines, if produced indefinitely, converge on the side on which the angles are less than two right angles and diverge on the side on which the angles are higher than two right angles”.
The proposition 28 states that: «If a straight line that meets two straight lines makes an exterior angle equal to the opposite interior angle on the same side, or if it makes the interior angles on the same side equal to two right angles, then the two straight lines are parallel».
Here uses the term «oposite interior angle» meaning the interior angle 2 which is alternate with respect to the exterior angle 1.
The two interior angles, the interior angle 1 and the interior angle 2, equal to 180 degrees already appears in the fifth postulate.
Understanding the terms mentioned above it is not necessary to add more comments to the 29 proposition : «If two straight lines are parallel, then a straight line that meets them makes the alternate angles equal, it makes the exterior angle equal to the opposite interior angle on the same side, and it makes the interior angles on the same side equal to two right angles».
But when it comes to making the demonstration with the angles, Euclid uses indistinctly the two sides of the line which to me seems is not very coherent with the style of the axiom 5. I think a clearer use of the angles on the demonstration of the proposition 29 would be this one:

In any case, to me is evident that the 5º postulate is not literally speaking about two right angles, it speaks about the degrees of two right angles, so 180 degrees. But it seems ulterior commentators of the fifth postulate who tried (and failed) to create a valid demonstration of it, considered the 180 degrees that result of the sum of the degrees of the «interior» angles of the same side were represented on the 5º postulate by two right angles, what is totally absurd, or they were not sufficiently aware that angles referred by the 5º postulate are only the interior angles of a same side (only one side) of the line that crosses the two parallel (or non parallel) lines.
But if it comes to demonstrating that the two lines are not actually parallel when the sum of the internal angles of the same side is not equal to 180, it could be said that since the moment that we displace one the line which is on the same quadratic coordinate (X or Y or Z) than the another line, we introduce a new and different plane ruled by a different kind of referential metric, the irrational plane instead of the rational one. So if those lines are in different planes, they cannot be considered parallels in virtue of the Euclid’s definition of parallels which requires that the two lines are on the same plane.
If it comes to demonstrating that the two lines actually converge when they are not parallel, I think it could be made by considering that the line (or lines) which is displaced with respect to the parallel (when the sum of the internal angles of the same side of the line are less or higher than 180 degrees) is already intersected with itself, considering its displaced position as the actual line and its previous non-displaced position as a virtual (non actually existent) line.

We see that the grey triangle inside of the straight lines c and d is equal to the white triangle inside the straight lines c and d. C and d and intersected by a diagonal lie.
So it implies, because of the equality principle, that the angle formed on the left side of a’ between the virtual line a and the actual line a’, must be equal to the angle that must exist on the right side of b on the convergence of the actual line b and the actual line a’. That actual point of convergence must necessarily exist at the right side of a’ and b, because it is the mirror consequence of the virtual point of convergence or self-convergence between the virtual line a and the actual line a’ (on the left side of a and a’). So a’ and b must converge at some point of their right sides.
The convergence point must be looked for at the beginning, not at the end, of the lines. Once it is fund as a virtual point of convergence, the final point of actual convergence can be logically deduced and so demonstrated from the initial and virtual convergence point.
The same can be said if we work with a cubic volume and a1 is one side of the base of the cube and a2 is the equivalent side of the ceiling of the cube and we displace a1 toward a’. In that case the initial convergence point will be also virtual but in a projective way between a’ and a2. The initial point of convergence created after displacing a1 towards a’ will be a projected point between a2 and a’.

Cheers.


Escribe tu comentario