(Antes de empezar quiero aclarar que este post, como todo el blog, es especulativo y heterodoxo. Quería mencionarlo por si alguien llega hasta aquí en busca de información para estudiar. Este blog no es para aprender ni estudiar, es para investigar, pensar, y tal vez inspirar).
Como sabrán, uno de los llamados problemas matemáticos del milenio es la «Conjetura de Hodge».
La web del instituto Clay http://www.claymath.org/millennium-problems/hodge-conjecture nos dice que «En el siglo XX los matemáticos descubrieron algunas maneras muy potentes de investigar las formas de objetos complicados. La idea básica es preguntarse hasta qué punto podemos aproximarnos a la forma de un objeto dado por medio de juntar simples bloques geométricos de una dimensión creciente».
(Es decir, se trata de usando bloques geométricos muy simples, de tamaño cada vez mayor, tratar de crear una figura lo más aproximada posible a una figura que tiene una forma compleja. El uso de infinitas – o infinitesimales – aproximaciones a una forma curva usando una forma rectilínea o cuadrangular es lo que hicieron ya Newton y Leibniz en el Siglo XVII dando origen el cálculo integral y diferencial).
Y sigue diciendo el enunciado que «esta técnica resultó tan útil que llegó a generalizarse, llevando a poderosas herramientas que permitieron a los matemáticos hacer grandes progresos en la catalogación de la variedad de objetos que encontraban en sus investigaciones».
(Cuando hablan de objetos se refieren a objetos algebraicos, es decir, estructuras abstractas en espacios abstractos).
«Desafortunadamente, los orígenes geométricos de esta forma de proceder llegaron a oscurecerse con esta generalización. En cierto sentido fue necesario añadir piezas que no tenían ninguna interpretación geométrica. La conjetura de Hodge afirma que para unos espacios particularmente agradables llamados ‘variedades algebraicas proyectivas’, las piezas llamadas ‘Ciclos de Hodge’ son, de hecho, combinaciones (lineares racionales) de piezas geométricas llamadas ‘ciclos algebraicos’.
Este párrafo trata de explicar la conjetura de Hodge de una forma accesible, pero – en principio – es completamente ininteligible para cualquier persona que no haya estudiado matemáticas. Porque, qué son las «variedades algebraicas proyectivas»? y qué son los «ciclos algebraicos»? Sin entender estas palabras técnicas no podemos entender qué es la conjetura de Hodge… También se usan en esta materia términos técnico como «manifolds» (que han traducido como «variedades») y submanifolds (subvariedades) que en principio no nos dicen nada. Pero vamos por partes.
Entonces los ciclos de Hodge son piezas geométricas cuya representación geométrica se desconoce. Pero se conjetura que sean combinaciones de otras piezas llamadas ciclos algebraicos. La representación geométrica de los ciclos algebraicos si es conocida. Así que alguna pista sí que tenemos. Un «ciclo» es una forma, y un ciclo algebraico puede ser una forma curva intersectada en varios puntos por una recta.
Hay una presentación de la conjetura de Hodge (que para mi no es muy entendible pero que nos da algunas pistas como esta del ciclo algebraico) que hizo un profesor americano, Daniel Freed, en la que muestra algunas representaciones de ciclos algebraicos: https://www.ma.utexas.edu/users/dafr/HodgeConjecture/netscape_noframes.html
Luego, podemos pensar que los ciclos de Hodge sobre los que trata su conjetura son combinaciones de este tipo de curvas.
Ahora tendríamos que saber qué es una variedad algebraica proyectiva, pero sabemos al menos que es un espacio que tiene una geometría que es armónica o simétrica ya que nos resulta agradable.
El vídeo de la conferencia del profesor Freed se puede ver aquí: http://claymath.msri.org/hodgeconjecture.mov
Realmente para mi no es entendible ninguna de las explicaciones que he buscado en internet sobre la conjetura, excepto esta de un profesor de la Universidad complutense de Madrid, Vicente Muñoz, que especialista en la Teoría de Hodge y he visto que al menos tiene otro trabajo sobre la materia, mucho más técnico (este es bastante más accesible porque no tiene álgebra):
https://ojs.uv.es/index.php/Metode/article/view/8253/10747
Para los matemáticos es muy difícil explicar esto en términos inteligibles porque no tienen una representación visual a la que referirse fuera de las ecuaciones algebraicas y tienen que buscar analogías o aproximaciones entendibles por los demás mortales.
Cuando leí la presentación del Instituto Clay sobre la Conjetura de Hodge me dio la impresión de que se estaban refiriendo, con diferentes términos, al problema de «Galois inverso» y al llamado «problema de la inmersión» de una extensión en otra extensión mayor.
Estos no son considerados problemas del milenio pero son temas surgidos a partir de la teoría de Galois que no están resueltos.
A la teoría de Galois ya me he referido en posts anteriores, surgió para explicar por qué las ecuaciones de más de un cuarto grado no pueden resolverse con operaciones matemáticas simples, como ya había demostrado Niels Abel. Y llega a la conclusión de que en las ecuaciones que llaman «polinomios» (por ejemplo Xˆ5 + Xˆ4 + Xˆ3 + Xˆ2 + X = 0) están presentes grupos de simetría, y que al llegar al quinto grado se produce una ruptura de la simetría y esto impide que la ecuación del quinto grado pueda resolverse como las de grado menor con simples operaciones matemáticas.
Cuando se trata de los grupos de Galois se usan los términos de «cuerpo» (que es como campo incial), extensión (que es un campo mayor que contiene al campo inicial), subcuerpos (subfields), que son los campos o extensiones intermedias que están dentro de una extensión mayor.
Ya comenté en los anteriores posts que envié las figuras a diferentes matemáticos y los pocos que me contestaron me dijeron no sabían decirme si esos diagramas eran o no grupos y extensiones de Galois. Y es que la teoría de Galois surgió y se desarrolló, como casi toda la matemática posterior de forma algebraica y abstracta. No hay prácticamente representaciones visuales de los grupos de simetría de Galois.
A mi me parecía que si lo eran porque con entender unos pocos conceptos, a qué le llaman extensión, a que le llaman cuerpo, a qué le llaman subextensión, inmersión, isomorfismo, homomorfismo, como tenía en menta la imagen de los diagramas era capaz de entender y seguir escritos a cerca de la teoría de Galois cuando no tenían álgebra, y hacer deducciones y anticipaciones.
El problema de Galois inverso viene a decir que si tenemos una extensión dada, o sea un campo mayor que contiene a un campo menor, cómo podemos saber cuáles son los subcampos intermedios entre la extensión mayor y el campo inicial que mantienen la misma imagen y estructura de simetría.
No se si esta es una interpretación libre que yo hago del problema pero yo lo entendí así. El problema de la inmersión es el mismo pero contemplado en vez de fuera a dentro de dentro a fuera: si tenemos una subextensión o un campo inicial, cómo podemos construir las subextensiones que median entre este y una extensión mayor dada.
El problema de Hodge a mi entender es el mismo, si tenemos un espacio o campo simétrico al que llamamos variedad algebraica proyectiva derivado de un campo inicial al que llamamos ciclo algebraico, cómo podemos saber si ese campo simétrico está formado por la combinación de unos campos menores a los que llamamos ciclos o formas algebraicos. Las combinaciones de esos campos menores serían los ciclos o formas de Hodge.
Pensé que si el Galois inverso y los ciclos de Hodge eran un mismo o parecido problema, ya se habrían dado cuenta y lo habrían relacionado. Y en efecto encontré que la que llaman «Conjetura de Tate», que es la versión aritmética de la conjetura de Hodge, describe los ciclos algebraicos de una variedad por medio de representaciones de Galois: https://en.wikipedia.org/wiki/Tate_conjecture
Uno de los temas que más discutí con algunas personas sobre los posts que escribí a cerca de Galois y las ecuaciones de quinto grado era que a mi no me cuadraba que las ecuaciones de quinto y mayor grado no pudieran resolverse con operaciones simples porque yo veía en los diagramas que la simetría se mantenía para todos los grados. Y llegué a la conclusión de que en la teoría de Galois se usa solo una ecuación polinómica mientras que yo estaba usando múltiples ecuaciones polinómicas combinadas.
A este respecto, me resultó revelador que en el trabajo de divulgación que he enlazado más arriba, el profesor Muñoz mencionase que «La conjetura de Hodge es difícil porque las subvariedades complejas son objetos muy rígidos (ya que están definidas por polinomios). De hecho, es muy difícil construir subvariedades complejas, y hay muy pocas. Probar que las subvariedades existen sin construirlas ha sido también difícil.
A mi modo de entender no es difícil, lo que pasa es que es extremadamente difícil cuando no se tiene una referencia visual de la geometría con la que se está trabajando algebraica o aritméticamente.
Entonces ahora voy a repetir en gran parte lo que dije en los posts anteriores con los diagramas, pero enfocándolo más hacia las combinaciones de los cuerpos iniciales y de las extensiones, que serían el problema de Hodge.
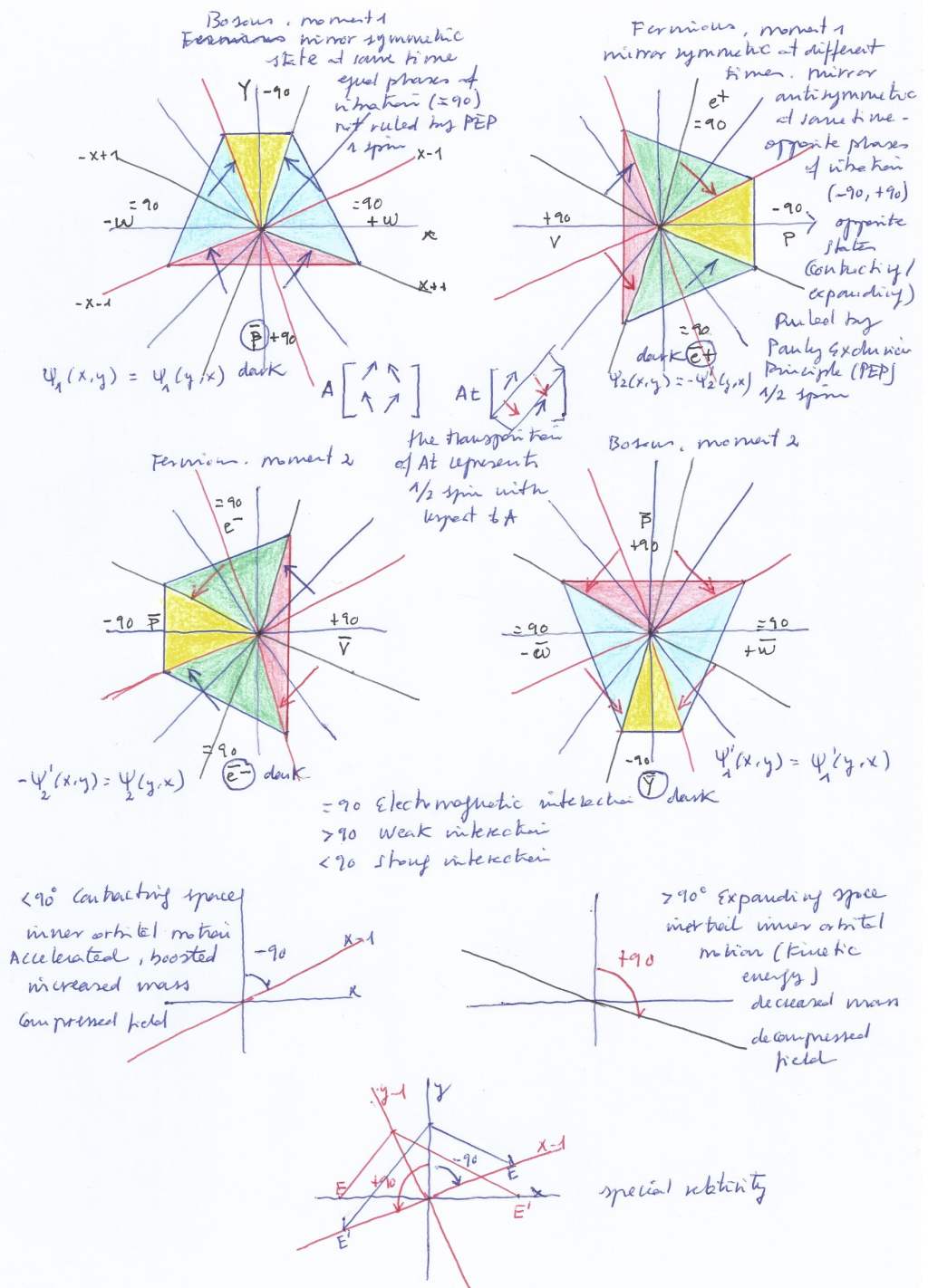
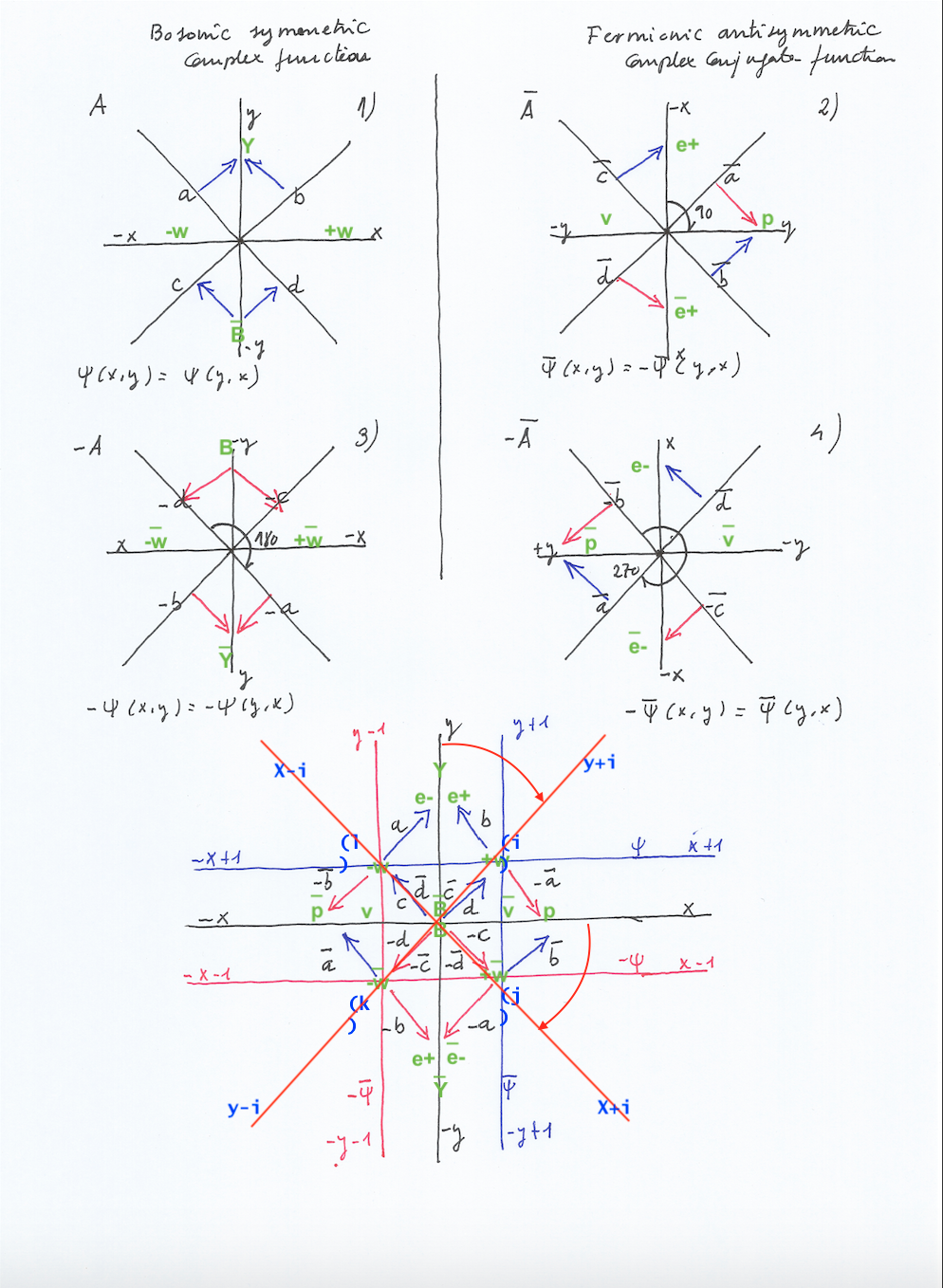
Como dije, voy a partir de una curva positiva y su curva conjugada (u opuesta) negativa, trazándolas desde el punto cero (el centro del círculo) hasta el punto rojo 1 en el eje de coordenadas Y.
Al hacerlo hemos encerrado un espacio que forma un cuerpo inicial de grado 1.
A continuación vamos a proyectar ese cuerpo inicial, prolongando las curvas de una forma rotacional (es decir siguiendo la dirección de las agujas del reloj y la dirección contraria a las agujas del reloj, haciendo rotar las coordenadas), elevando el grado hasta que las curvas opuestas converjan en un punto. Así podemos prolongarlas al punto 2 de Z, luego al punto 3 de Y, luego al punto 4 de Z hasta que convergen en el punto 5 de Y –
El espacio que encierran las dos curvas ahora es una extensión invertida de grado 5 que contiene al cuerpo inicial de grado 1.
Si volvemos a prolongar (o proyectar el cuerpo inicial prolongando) las curvas hasta la siguiente convergencia que tiene lugar en el grado 9 en Y+, tenemos esta nueva extensión de grado nueve que comprende a la subextensión de grado 5 y al cuerpo inicial de grado 1:
Podemos seguir creando extensiones cada vez mayores indefinidamente, pero el problema que se plantea ahora es el de Galois inverso, es decir, cómo podemos crear, si es que se puede, o reconocer si es que ya existen, las subextensiones que pensamos que tendría haber – si hay una continuidad en la simetría – entre la extensión mayor de grado 9 y la extensión menor de grado 5, y entre esta y el cuerpo inicial de grado 1.
No parece que se pueda hacer proyectando de la forma que lo hemos hecho un único cuerpo inicial formado por dos curvas opuestas (conjugadas). Para formar las extensiones intermedias necesitaríamos replicar el cuerpo inicial de grado 1 creando otros cuerpos de grado que sean imagen del primero. Tenemos varias formas de hacer esta replicación siempre el reflejo de la estructura de grado 1, es decir creando los cuerpos que siguen su simetría y simetría invertida de espejo.
Así, vamos a continuar creando dos nuevos cuerpos de grado 1 en las coordenadas Z que van a ser el reflejo del cuerpo real de grado 1 en Y. (A los campos que están sobre las coordenadas Z se les llama complejos con respecto a los que están en las coordenadas cuadráticas X Y que se llaman reales).
Entonces tenemos un cuerpo real de grado 1 en Y+, un cuerpo complejo en Z + y su cuerpo complejo conjugado en Z – (Los dos campos en Z son complejos y a uno se le llama conjugado del otro al tener su signo opuesto).
Ahora, prolongando las dos curvas del cuerpo de grado 1 complejo y su conjugado, podemos obtener nuevas extensiones que van a formar un grupo de simetrías distinto del grupo que forman las extensiones que formamos prolongando las curvas del cuerpo real de grado 1.
Si observamos esta figura podemos ver cómo se han formado las extensiones (esto es, vamos a analizar la geometría que hemos construido).
Con la curva + del cuerpo complejo + de grado 1 y con la curva – del cuerpo complejo – de grado 1 hemos formado una extensión real de grado 2 en Y +
Con las curvas + y – del cuerpo complejo + de grado 1 hemos formado una extensión compleja – (e invertida) de grado 5.
Con las curvas + y – del cuerpo complejo – de grado 1 hemos formado una extensión compleja + (e invertida) de grado 5.
Con la curva + del cuerpo complejo + de grado 1 y con la curva – del cuerpo real + de grado 1 hemos formado una extensión compleja + de grado intermedio entre 1 y 2 en una nueva coordenada Z’+.
Con la curva – del cuerpo complejo – de grado 1 y con la curva + del cuerpo real + de grado 1 hemos formado una extensión compleja – (conjugada de la anterior) de grado intermedio entre 1 y 2 en una nueva coordenada Z’-.
Estas dos últimas extensiones que hemos formado combinando una parte real y otra compleja son muy interesantes, porque en ellas el cuerpo real de grado 1 Y+ está actuando como un cuerpo complejo conjugado del otro cuerpo complejo de grado 1 en Z. Esto es así porque lo que hemos hecho en realidad ha sido rotar el eje Y+ hacia Z-, y el eje Z+ hacia Y+ de manera que hemos variado el centro de simetría de esas dos nuevas extensiones complejas que no tienen un cuerpo real entre medias. Además, al hacerlo así hemos creado un subcuerpo de grado inferior a 1 entre el cuerpo de grado 1 real y el complejo. (Este subcuerpo es complejo respecto a la coordenada Y, pero real respecto a la coordenada desplazada, y será trivial respecto a la extensión que hemos creado en esa coordenada desplazada.
Entonces ese subcuerpo en la coordenada desplazada es muy interesante porque es como un tipo de estructura inversa: antes, del cuerpo inicial de grado 1 real en Y creamos dos cuerpos complejos de signo opuesto, en Z+ y Z-, mientras que aquí, de un cuerpo complejo en Z y uno real conjugado en Y (que es complejo respecto a la coordenada desplazada que hace de centro de simetría) creamos un subcuerpo de grado menor que el inicial y que será real respecto a la coordenada desplazada o complejo si tomamos como referencia la coordenada Y).
En este sentido, si pudiéramos llamar «derivada» a la extensión que hemos creado en la coordenada intermedia desplazada, el subcampo que hemos creado al mismo tiempo sería la «antiderivada» o «integral», lo que nos permite también hablar en términos de ecuaciones diferenciales.
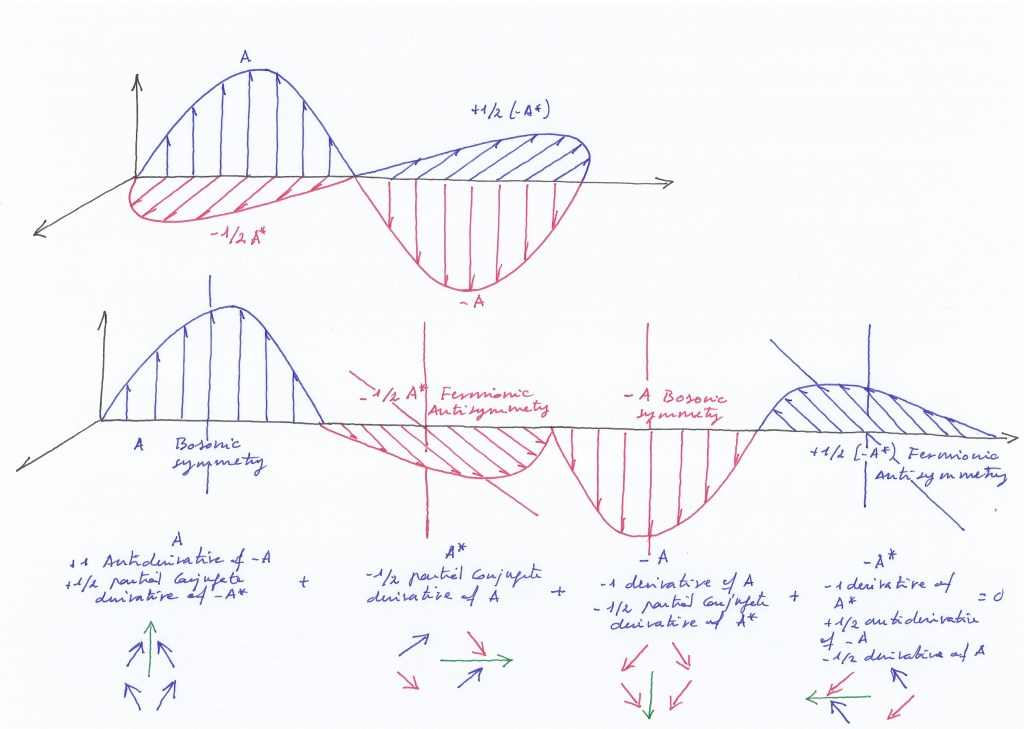
Para que se vea más claro (porque en los otros diagramas casi no se aprecia), en el siguiente diagrama he representado coloreada en negro la extensión «derivada» de la combinación de los cuerpos ab, y coloreado en verde el subcuerpo «antiderivado» de ab y que sería su integral. (Para mi lo contrario de derivar no es deshacer la derivación para volver a las curvas iniciales):
la derivada de los campos ab es la extensión que construimos prolongando la curva + de a y la curva – de b. (La extensión es la parte coloreada en negro, más el campo a y el campo b. La integral de los campos ab es la operación inversa de la derivada, o sea su antiderivada: así, en vez de obtener el campo que se deriva de ab, obtenemos el subcampo (coloreado en verde) del cual se han derivado a y b (las curvas + y – de ab).
(Extensión es un campo mayor que contiene otro menor u otros menores. En este caso la extensión se deriva al prolongar o proyectar las curvas + y – de las subextensiones o campos iniciales a y b, que determinan o «restringen» la estructura de la extensión).
Por otra parte, se dice que el cuerpo real de grado 1 en Y+ es «trivial» con respecto a la extensión real de grado 2 en Y + porque la estructura de esa extensión de grado 2 no está determinada o restringida por la estructura (tamaño y posición) del cuerpo de grado 1. La extensión de grado 2 viene determinada por los dos cuerpos complejos de grado 1.
Sin embargo el cuerpo de grado 1 no es trivial con respecto a estas dos nuevas extensiones complejas (cuyo centro de simetría está entre Y y Z), ya que en ellas el cuerpo real de grado 1 se comporta como un cuerpo complejo referido al eje rotado, conjugado del cuerpo complejo de grado 1.
[Si la función (o funciones) que estamos representando en el diagrama de arriba fuera la función Z de Riemann, si contemplamos la estructura desde el punto de vista de Y desplazada vemos que la integral de ab es trivial respecto de la derivada o extensión de ab (ya que no detrmina su estrutura) pero es no trivial respecto al cuerpo real «a» y respecto al cuerpo complejo «b» cuya estructura determina o restringe en su mitad. Al mismo tiempo, esa integral es compleja respecto al eje de simetría de los cuerpos «a» en Y o «b» en Z, pero es real respecto a la coordenada Y desplazada que es el eje de simetría de la extensión o derivada de ab. De manera que la integral es una parte real y trivial respecto de la derivada compleja de ab, pero esa integral es es una parte compleja y no trivial respecto a su derivada real en Y y a su derivada compleja en Z. (Desde el punto de vista de la integral real, en el eje desplazado, sus extensiones derivadas «a» en Y y «b» en Z son complejas).
En este sentido podríamos decir que dado que en el eje de coordenadas de Y desplazada en el que convergen tanto la derivada de ab como su integral, el valor del punto de convergencia de las curvas es cero, y dado que ese eje desplazado de Y hacia Z coincide con 1/2 del plano complejo (el plano complejo sería el plano entre la coordenada Y y la coordenada Z), como el valor de la integral es no trivial respecto a los cuerpos de grado 1 a y b, estaríamos confirmando para este caso la hipótesis de Riemann según la cuál la parte real de cualquier cero no trivial de la función Z de Riemann es 1/2. EL punto cero pasaría entonces por 1/2 del plano complejo.
No sé si es mucho especular, pero este inciso no me parece muy desencaminado. Si leemos el discurso de Riemann «Sobre las hipótesis en las que se fundamentan las bases de la geometría» podemos ver que en su forma de pensar o imaginar el espacio está siguiendo un tipo de estructuras muy parecidas a las que estamos representando aquí, y podemos seguir en muchos párrafos su razonamiento teniendo presentes las imágenes de los diagramas anteriores y cómo se van formando. (En Riemann, como en Hodge, los términos extensiones, cuerpos, subextensiones, son cambiados por «variedades» y «subvariedades» que es como han traducido del inglés «manifolds», términos esos que a mi no me gustan por opacos. Habría que ver qué quería decir el término original alemán como era usado en el siglo XIX).]
Por otra parte, siguiendo con la creación de extensiones, podemos ver todas las combinaciones darán lugar a los diferentes grupos de simetría que llamaremos «de Galois» y que son los que seguirán las diferentes extensiones, y también darán lugar a los «ciclos» o formas «de Hodge» (que sabemos, en forma general, son combinaciones de curvas algebraicas) que serán las extensiones y grupos de extensiones y extensiones formadas por esas combinaciones hasta formar un espacio en el que hay una misma estructura de simetría continuada.
Ahora podemos volver a replicar los cuerpos de grado 1 con sus cuerpos reflejos invertidos, y al prolongarlos obtendremos las extensiones que tienen una simetría de espejo con respecto a las anteriores:
Podemos seguir de esta manera completando la figura:
Otra de las opciones que tenemos para formar extensiones es replicar las dos curvas del cuerpo real de grado 1 con sus curvas inversas:
Si formamos las extensiones que surgen de prolongar las dos curvas conjugadas (de signo opuesto) que hemos formado en la coordenada X, tendremos un nuevo grupo de extensiones. La primera extensión que se forma es de grado 3 en Y+ y la siguiente una extensión invertida de grado 7 en Y –
Es interesante ver que en la coordenada Y – han coincidido de forma consecutiva dos extensiones primas, la de grado 5 y la de grado 7 que siguen grupos de simetría diferentes. Por eso vamos a investigar un poco más y ver cómo se distribuyen los números primos de esta manera.
Para evitar las interferencias entre primos que siguen a cada grupo de simetría, vamos a tomar sólo las extensiones que siguen al grupo que surge de prolongar la mitad de los dos cuerpos conjugados de grado 1 en X. (Esto ya lo he comentado también en los anteriores posts):
Si tomamos las extensiones reales que se forman en Y + e Y – al prolongar las curvas + y negativa de los cuerpos + y – de grado 1 en X (inversos respecto a las curvas – y + del cuerpo real en Y+) vemos que las extensiones que son primas se distribuyen de esta manera:
Si confrontamos las extensiones en dos filas vemos que se organizan en grupos de 6 primos y que existe una relación de simetría de espejo entre las parejas opuestas:
Cada elemento suma con su opuesto 90.
Este mismo tipo de correspondencia la encontramos ejemplificada en este manual de álgebra abstracta hablando de la correspondencia entre las extensiones de Galois. Que justamente aparezca esta simetría creando lo que pienso que son extensiones de Galois, pues para mi es indicativo de que no voy muy desencaminado.
Esto es como una labor en parte detectivesca en la que hay que seguir pequeñas pistas que nos sirven de traducción o traslación entre el mundo de estructuras abstractas que han creado los matemáticos y el mundo natural. La situación para mi es como la que surgiría si unos músicos se pusieran a escribir canciones para distintos instrumentos pero no se dan cuenta de que casi todos están componiendo la misma melodía porque nadie ha escuchado nunca esa canción. Pero son capaces de intuir y conjeturar que la canción debería ser reconocible combinando esas piezas musicales que llaman ciclos algebraicos.
Imagínense ustedes el caos que se generaría si llegara alguien que nunca ha escuchado tampoco la canción y se pusiera a describir con ella algo que tampoco ha visto nunca como con los núcleos atómicos y al resultado lo llaman «mecánica cuántica».
Pero sigamos con los primos que es una cosa muy bonita. Si además añadimos dos líneas con las extensiones primas que surgen de proyectar o prolongar las dos curvas + y – del cuerpo real de grado 1, vemos que la distribución sigue un cierto orden:
Por otra parte, los diagramas los he representado con curvas pero también pueden representarse con rectas de esta manera:
Otra manera de representar las extensiones es esta:
En todas estas figuras he seguido un mismo intervalo que viene dado por el segmento que se obtiene al medir en la coordenada Z desde el punto cero hasta el centro del cuadrado de 0.25, que al repetirlo llega hasta el centro del cuadrado de area 1 y luego al de área 4, etc. Como es la mitad de la hipotenusa de los cuadrados de raíz racional sería un intervalo irracional. Pero también podemos crear los cuerpos y extensiones que siguen un intervalo diferente que no es directamente comparable con el otro, como es el que se obtiene de medir desde el punto cero hasta el centro de simetría del cuadrado de raíz irracional 0.50, y luego l repetirlo hasta el cuadrado de 2, etc.
Combinando estos intervalos también se crean extensiones mixtas. Además los intervalos racional e irracional convergen en los grados 5 y 7 respectivamente, de forma periódica.
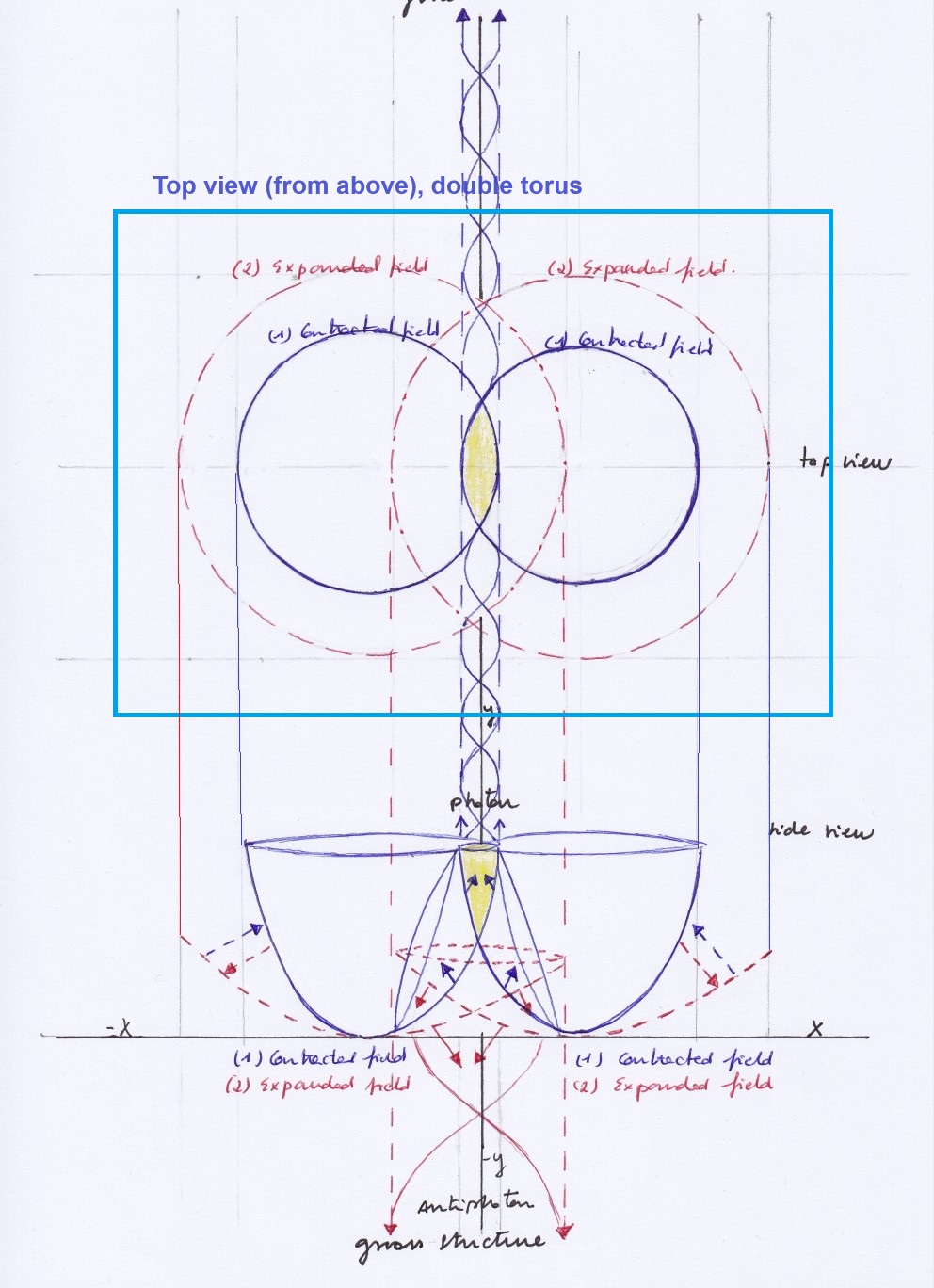
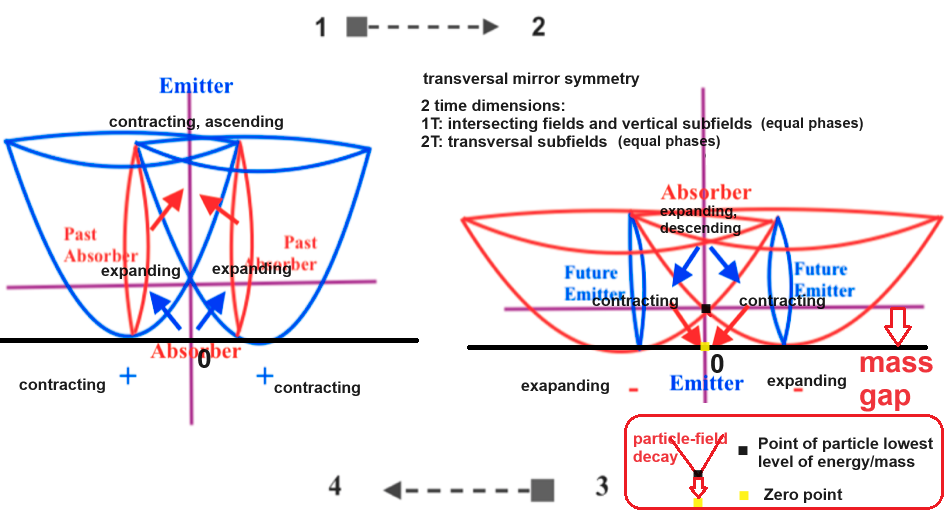
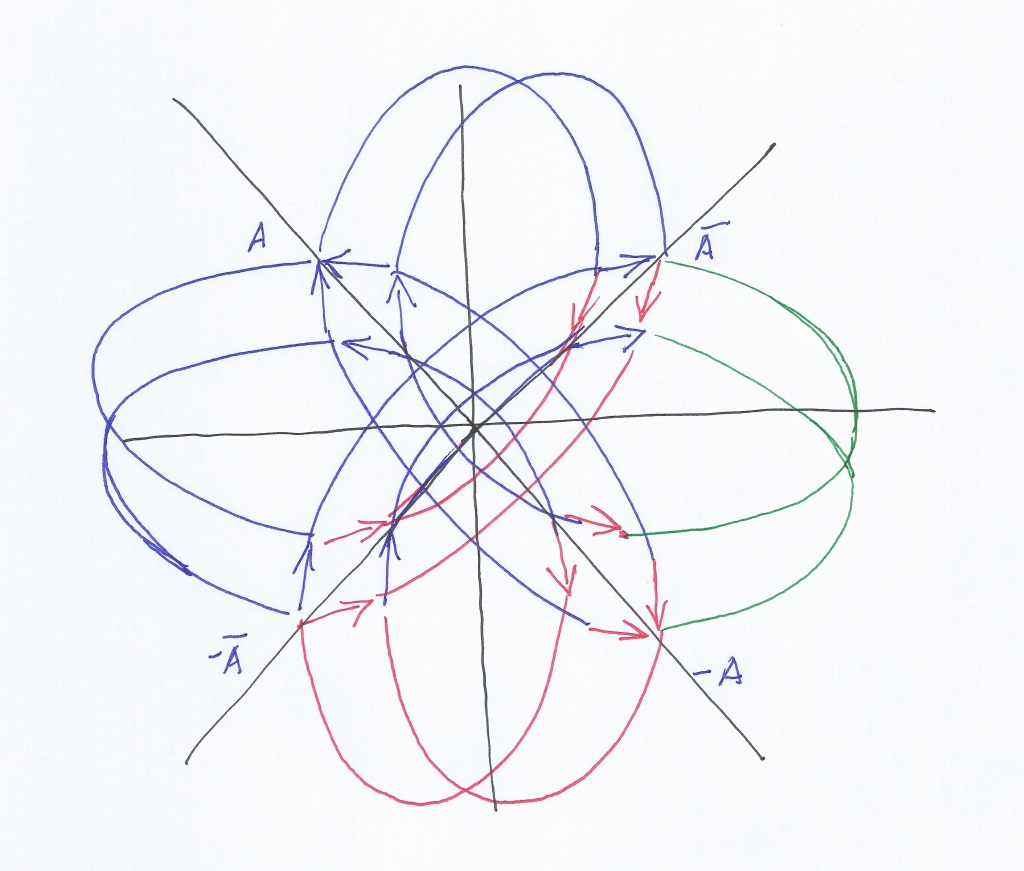
Por lo que se refiere a la representación en 3D, las figuras que creé para explicar el modelo atómico estarían también relacionadas con esta materia (y con la geometría imaginaria de Lobachevsky). Se trata de al menos dos campos intersectados que varían con fase igual u opuesta, creando nuevos campos en y por su intersección. Los núcleos atómicos serían entonces los campos que surgen por combinación de otros campos que interaccionan entre sí al intersectar:
Podemos preguntarnos finalmente: entonces, es correcta la conjetura de Hodge?
En el artículo antes mencionado del profesor Vicente Muñoz nos explica la teoría de Hodge haciendo un símil muy bonito con la disipación del calor que se produciría a partir de un punto calorífico y cómo se distribuye por el espacio por medio de funciones armónicas:
Y al final dice que la potente teoría de Hodge afirma que cualquier tipo de homología (en un n variedad cerrada, finita y sin bordes) es dada por una sola forma armónica, siguiendo un proceso análogo al de la disipación de la ecuación del calor.
Podemos pensar en el cuerpo inicial real de grado 1 como un punto primero de calor que se va disipando al distribuirse por el espacio y a los cuerpos de grado 1 que creamos por medio de sus reflejos y reflejos invertidos como los armónicos de ese cuerpo inicial. Pero no haría falta recurrir a explicaciones analógicas si sabemos cómo es la geometría de los ciclos de Hodge. Para mi esa geometría es la combinación de las extensiones de esos cuerpos complejos entre sí y con el cuerpo real, del que serían variedades armónicas, las que permiten crear las estructuras que son llamadas (en mi opinión) extensiones y subextensiones de Galois o (en mi opinión también) ciclos de Hodge.
Estos diagramas no son una prueba ni una refutación de la teoría de Hodge pero sí sirven en mi opinión para darse cuenta de sobre qué estamos hablando al tratar con grupos de Galois o ciclos de Hodge.
Pienso que puede que incluso que la refutación o confirmación algebraica ya la tengan hecha y ni siquiera se hayan dado cuenta, porque los matemáticos han creado muchas estructuras algebraicas diferentes para atacar problemas iguales o distintos. Y como cada uno o su escuela crean términos técnicos y opacos diferentes parece que se trate de cosas distintas. Así por ejemplo creo que fue Shafarevich quien ya demostró la continuidad de la simetría en cualquier grado cuando se trata de números complejos. Aquí estamos usando números hipercomplejos (a partir de cuatro, los cuaterniones, los llaman hipercomplejos), por medio de la rotación de las coordenadas, lo que da lugar a la creación de nuevos centros de simetría en las coordenadas desplazadas y a espacios reales, complejos y mixtos (en parte real y en parte complejos, dependiendo de cómo se contemplen).
También está relacionado con lo mismo en mi opinión lo que llaman ecuaciones diferenciales fucsianas y sus grupos de monodromía, que es sobre lo que voy a investigar a continuación.
Voy a poner a continuación algunas otras figuras que quizás puedan aclarar más cómo se construye la combinación de las extensiones, paso a paso:
De entre los diferentes libros que consulté buscando representacione geométricas de los grupos de Galois, estas fueron las únicas que encontré en el libro de los profesores Malle y Matzat, que aparecen en su libro “Inverse Galois Theory”:
Un cordial saludo.
Nota: Los anuncios publicitarios que pueden aparecer abajo los pone Worpress ya que al ser este es un blog gratuito, aunque la url sea personalizada, ellos ponen la publicidad que quieren en su beneficio.














































Escribe tu comentario