Hi friends. I hope you’re doing well.
I watched this interesting conference of professor of theoretical physics David Gross about the Yang Mills theory and the «mass gap» Millennium problem and decided to write about it here:
Reading or hearing anything about quantum mechanics from professional physicists can be a tough task because of the uncountable number of very opaque terms physicists and mathematicians use, with almost no image, from their abstract algebraic developments: «Yang Milles theory», «Lagrangian», «Hamiltonian», «Manifolds and Riemann spaces», «Cohomology», «Topologic Vectorial spaces», «Gauge theories», «Minkowski spaces», Bell inequalities», «Lorentz transformations», «vector bundles», «Cobordian», «Moduli spaces», «Asymptotic freedom», «Isospin» or isotopic spin», «Galois groups», «Lie groups», «Poincaré groups», «Abelian and non abelian groups», QCD, QFT, AQFT, TQFT… and so on. It’s something endless.
Even without using algebra, their abstract developments can be conceptually explained and understood with a lot of difficulties. But there are always some little clues that will let use translate those terms to our visual and conceptually logic representations. For example, the term «gauge» and «topological vectorial spaces» can be easily understood in this way. Even if you think you understand nothing, you always are going to find an Ariadna thread.
One clue about Yang Mills theory is that it’s about strong interactions. Knowing what strong interactions conceptually and visually are, we can deduce more or less the where that theory is going to go.
Professor Gross presents Yang Mills theory (failing when it comes to describing the atom) a as possibly real theory that appears to be separate from Quantum ChromoDynamics, which for him would be a non real theory (a tool that does not respond to reality although it’s useful to make calculations) that let us describe the atom.
That surprised me because some days ago I took a look to a thesis (very difficult to read for me because its algebra) titled «Des théories quantiques de champ topologiques aux théories de jauge supersymétriques» by Guillaume Bossard that relates Yang Mills theory with vectorial spaces to https://tel.archives-ouvertes.fr/tel-00191113/document
I had naturally related Quantum Chromodinamics with vectorial spaces because to me what QCD calls «quarks» representing them with vectors, are topological vector spaces as I will show later.
Also, this interesting article form the Britannica Encyclopaedia gives us some clues: https://www.britannica.com/science/mathematics/Mathematical-physics-and-the-theory-of-groups#ref66034
Here you have the link from the Clay institute with the Mass gap problem enunciated: http://www.claymath.org/millennium-problems/yang%E2%80%93mills-and-mass-gap
You can take a look to the originary paper of Yang and Mills «Conservation of Isotopic Spin and Isotopic Gauge Invariance» here: https://journals.aps.org/pr/pdf/10.1103/PhysRev.96.191
And looking for that title you can find other articles that can you give you some more clues, for example this one speaking about the isospin: http://www.applet-magic.com/yangmills.htm
If you have already read this blog you will know most of the content I’m going to write here.
I think the electromagnetic properties of space only appear when at least two vibrating spaces get intersected (or partially merged). By spaces or fields I mean longitudinal waves or vibrating vortices.
Because of that intersection, there are going to be 3 subspaces in the concave side of the dual system and a subspace in its convex side whose physical properties are going to be different depending on the phases of vibration of the intersecting spaces that periodically synchronize and desynchronize.
(I think manifolds in the original Riemann geometry do not imply «overlapping» spaces but physically intersecting or partially merged spaces that form shared subspaces because of their intersection).
The interactions that let the dual system of intersecting spaces and its shared nucleus of subspaces remain united is going to be the inner orbital motion of each subspace. The strongest interaction will occur when the two intersecting spaces contract at the same moment, and the lowest interaction when they both expand at the same moment. That would explain why strong interactions take place in smaller distances, (as the subspace inside of which the inner (magnetic?) orbital motion or kinetic energy is contracted), while the lower interaction occurs in larger distances (as the subspace whose inner orbital that acts as a «chemical» bond is expanded).
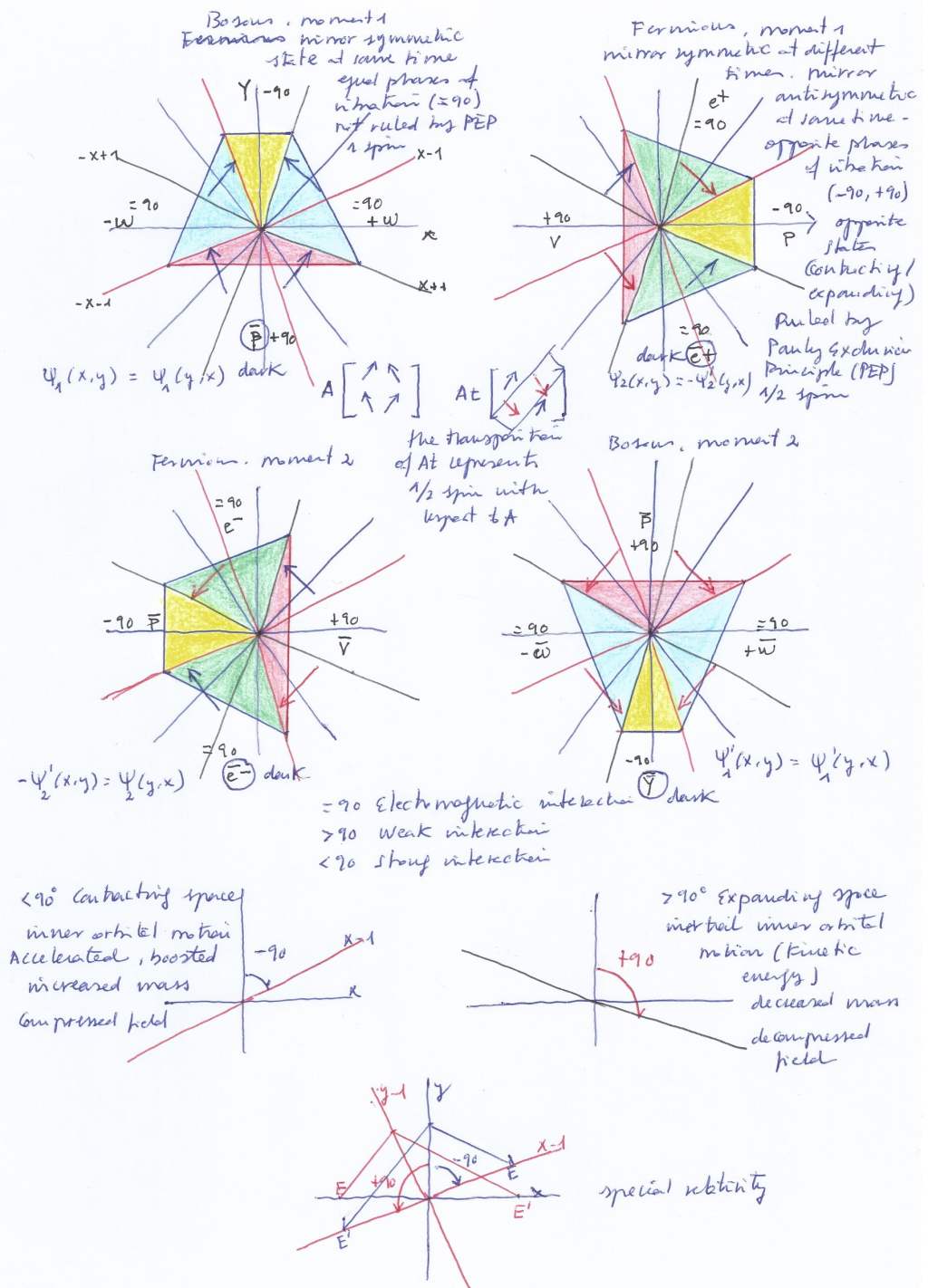
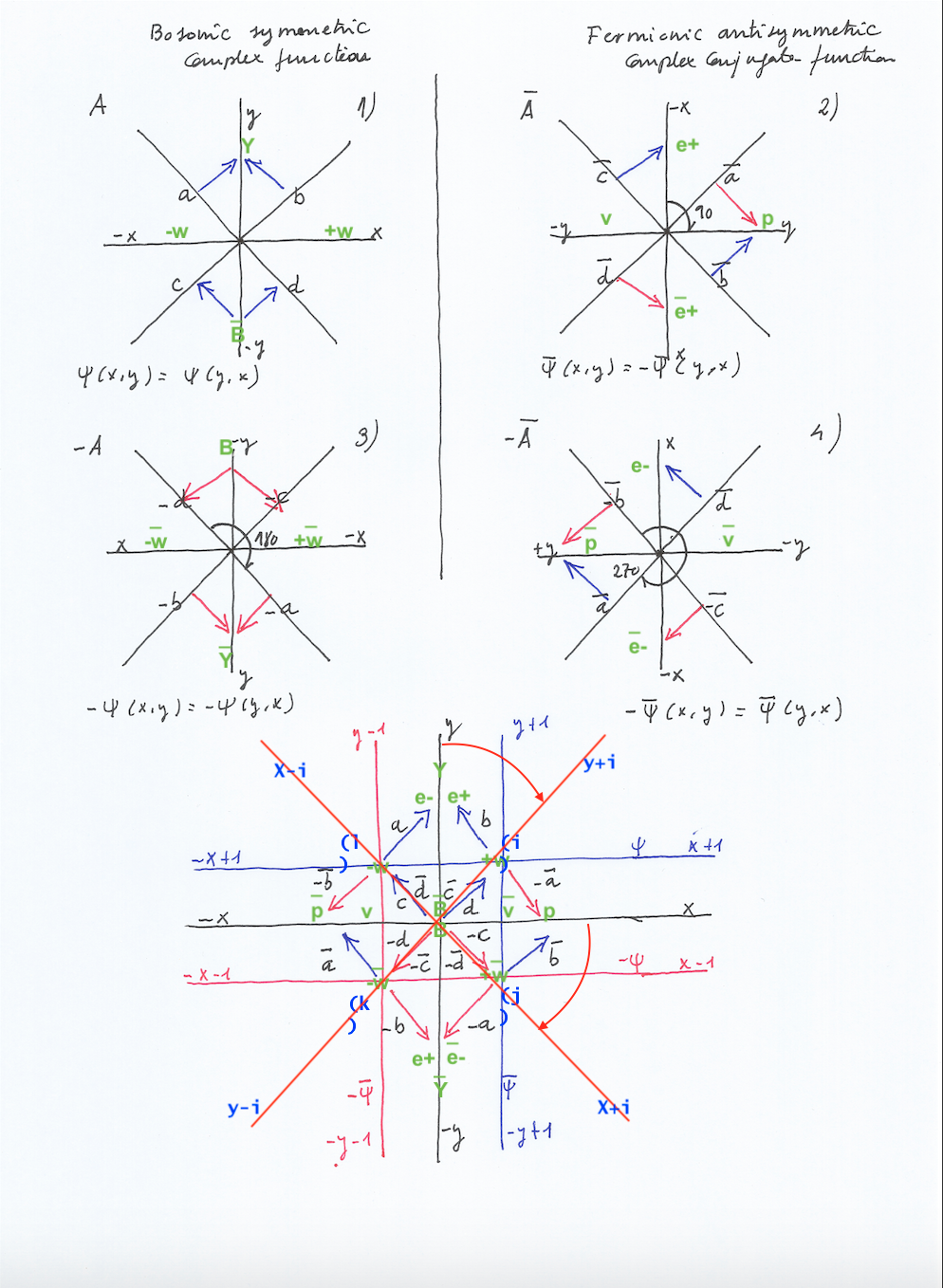
With equal phases of vibration, the orthogonal subspace is going to move left to right towards the side of the system where one intersecting space contracts (while the other one expands). This subspace will act as an electron when moving towards left and will become a positron when a moment later it will move towards right. Being its own antiparticle (although at different moments) this subspace will be a Majorana antimatter. When the subspace is at the left side as electron, it can be thought it exists as a virtual positron at the right handed side in the sense that although now it does not actually exist there, it virtually has the potential of becoming existent there a moment later.
I considered it as a fermion following the Pauli Exclusion principle, because the Majorana subfield could not be at two mirror symmetric places at the same moment. In this sense I think the PEP must be interpreted only in terms of mirror symmetric particles. Quantum states in this context are the state of a subspace of being expanded or contracted, which it partially changes in this context when the subspace is passing by the vertical axis while traveling left to right or right to left.
We could consider the inverted subspace existing at the convex side of the intersection that would be mirror symmetric with respect to the orthogonal subspace. And in that case the mentioned subspace could not be considered a fermion but a boson not ruled by the Pauli Exclusion Principle following the Bose Einstein statistics. If we are an observer placed in the concave side of the system, its convex side (the tension of its curvature, its inner orbital kinetic energy and the pushing force it causes when moving left to right will be directly undetectable – and so «dark» – for us.
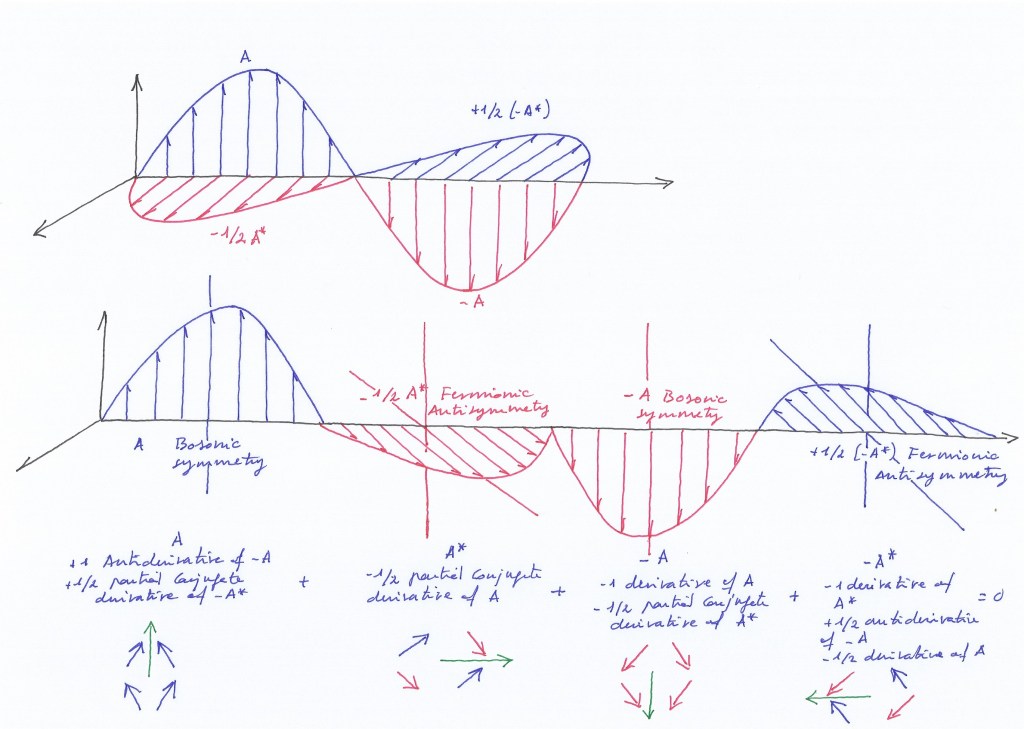
The difference between 1/2 and 1 integral spin that respectively correspond to fermions and bosons, I think must be interpreted also in terms of mirror symmetry (be aware that the quantum mechanic models do not know the topology of the system, their approach is probabilistic; I think then 1 integral spin in the case of bosons is given by the -1/2 and +1/2 spin of the left and right transversal subspaces, when being both contracted or expanded; while the -1/2 or +1/2 spin in the case of fermions is given by the transversal subspaces that only will have mirror symmetry at different moments; we only could add the -1/2 neutron and the +1/2 proton if they existed contracted at the same moment. (But in the context of equal phases when the transversal bosons appears, the vertically ascending subspace we considered a (non Majorana) fermion that creates the photon, is going to have inside a double spin).
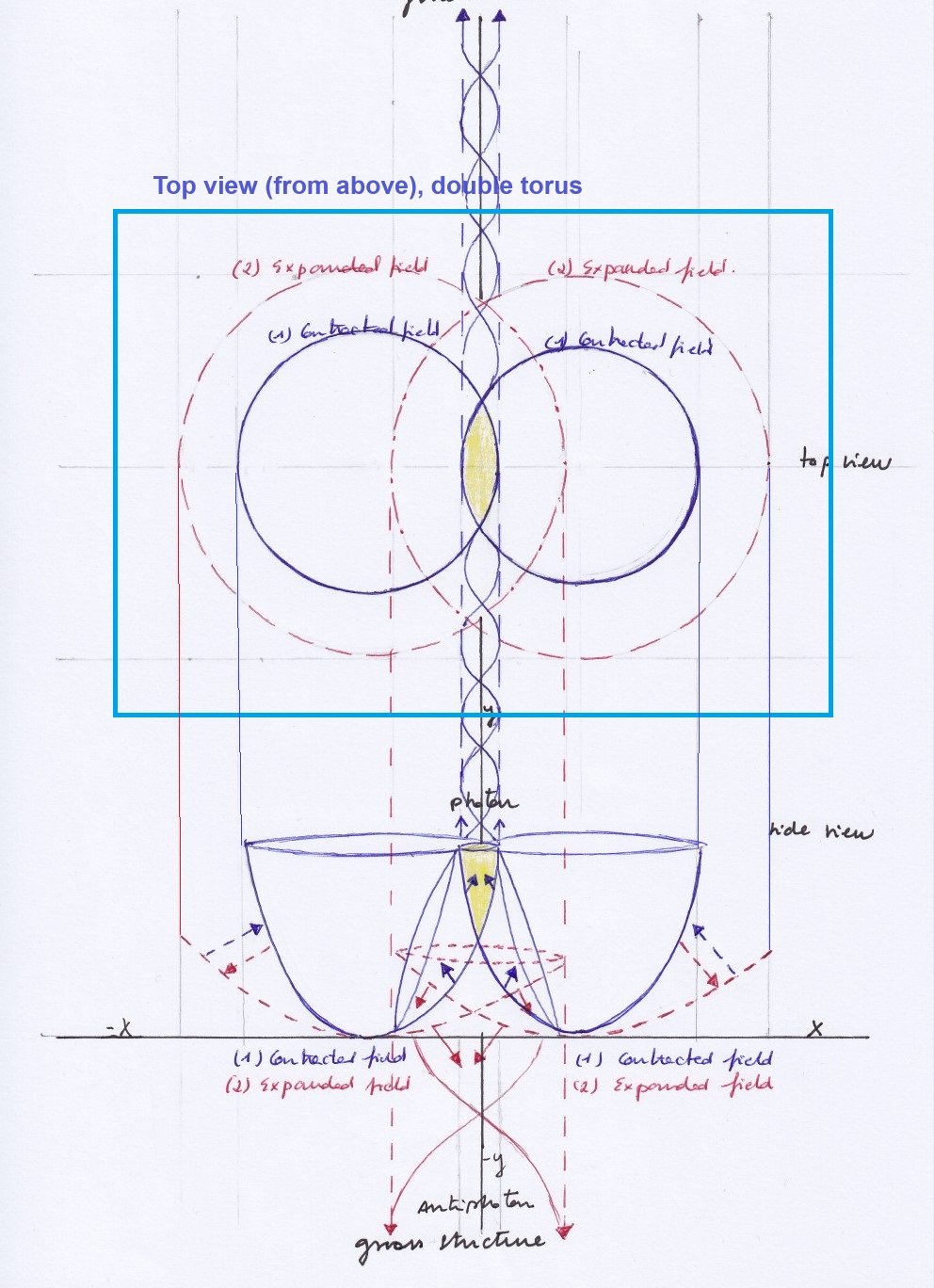
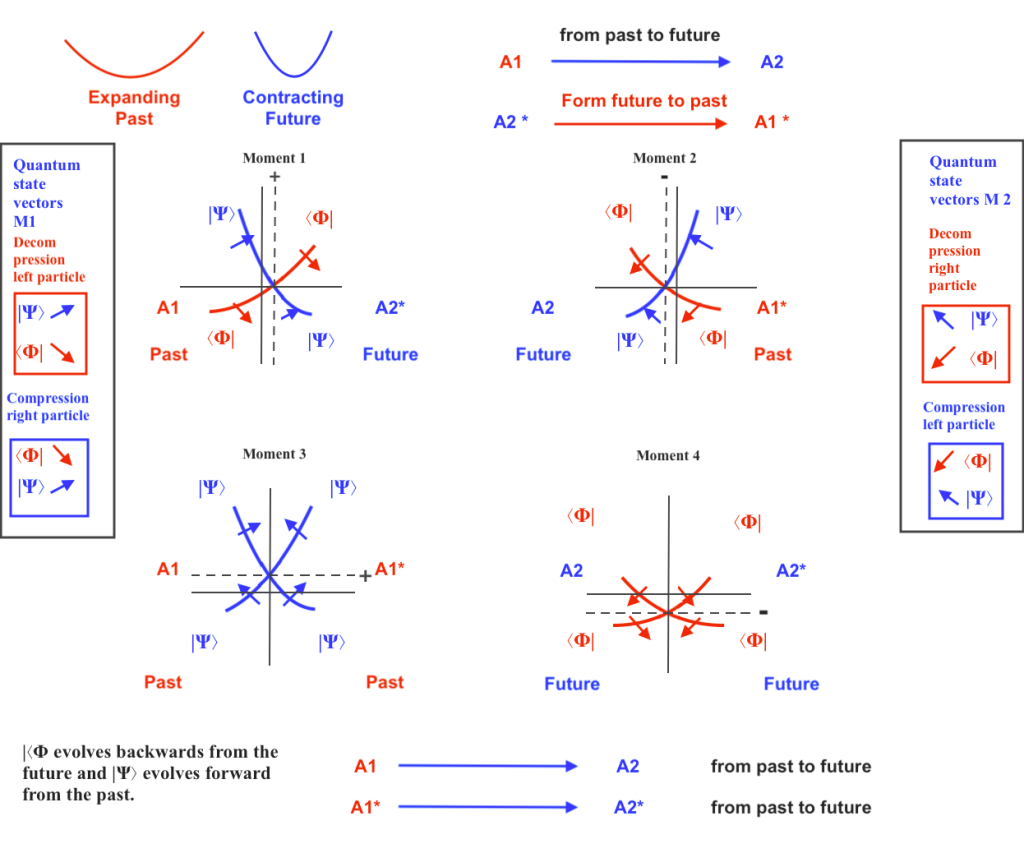
When the phases of vibration synchronize becoming equal, the orthogonal subspace will not move pendularly left to right but upwards and downwards: when the two intersecting spaces contract at the same moment, the orthogonal subspace will ascend through the vertical axis getting contracted with a double helix of opposite spins orbitally rotating inside. Its ascending pushing force will create a photon. A moment later, when the two intersecting spaces expand, the ascending subspace will descend, getting expanded; its previous pushing force and its inner kinetic energy will be mainly lost. This loss of energy could be interpreted as a mass gap issue. The spectrum that the orthogonal subfield emitted so far with opposite phases in a continuous way, is going to be emitted now in a pulsating or quantum way. When the decay of the ascending subfield occurs, nothing is going to be emitted by the system in the orthogonal realm in the concave side, but a force and kinetic energy equal than the lost ones is going to emerge inverted in the convex side of the system creating an antiphoton.
This image shows the non interrupted continuity of spectrums emitted when the [phases of vibration are opposite:
And this figure next figure illustrate how the mass or energy gap, the apparent discontinuity of the emitted spectrums would occur when – with same phases of vibration – the ascending subspace decays in the concave side of the system while an inverted pushing force and orbital kinetic energy takes place at the convex side of the system:
This figure illustrate how the mass or energy gap, the apparent discontinuity of the emitted spectrums would occur when the ascending subspace decays and an inverted pushing force and orbital kinetic energy takes place at the convex side of the system:
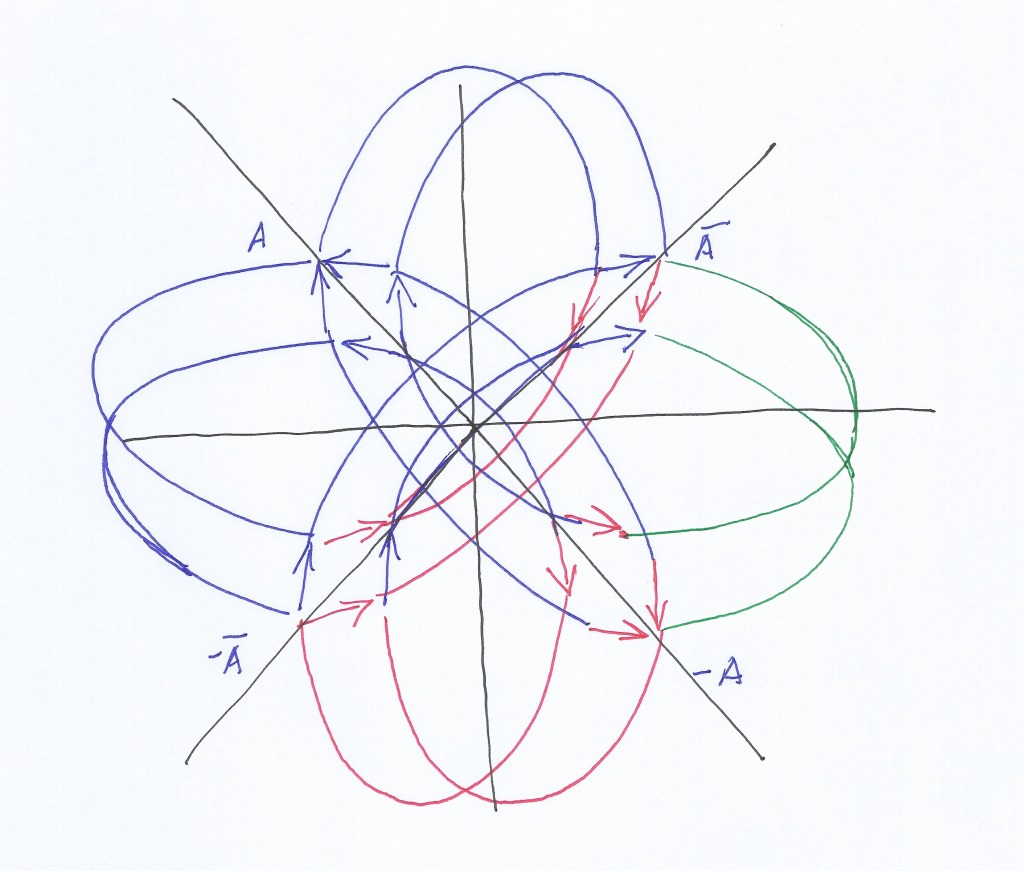
I’ve recently found a similar diagram although in 2D representing the Majorana fermion as the product of two intersecting wave functions in a work by Vicent Mourik titled “Signatures of Majorana fermions in hybrid superconductor – semiconductor nanowire devices”:
Although the ascending and descending orthogonal subspace is a fermion it’s not a Majorana subspace as it’s not its same antimatter. Its counter subspace would be the inverted subspace that exists at the convex side of the intersection (which follows an opposite phase).
I also recently found a similar diagram in John Bell’s «The Nouvelle Cuisine» article, in the context of locality and nonlocality in quantum mechanics, with a different purpose. I attached it below because I read in an article by Gábor Hofer-Szabó, «On the relation between the probabilistic characterization of the common cause and Bell’s notion of local causality“, that he called them «isotone nets» generated by «local σ-subalgebras of a Boolean σ-algebra Σ», which seems to be a technique that is used in Algebraic Quantum Field Theories.
I rotated them to make them more familiar to the figures of this blog:
But the dual system also accepts two transversal subspaces in the horizontal axis. I think the transversal location of inner spaces has already been used in Kaluza Klein and in Kalaby Yau developments, although in a different way:
When the phases of vibration are opposite or antisymmetric, the left and right transversal subspaces are going to have as well opposite phases between them, (maybe the term «decoherent»could be used here), and are going to follow the same phase, (maybe the term «coherent» could be used here), with respect to the space they are inside of.
So, when the left intersecting space contracts and the right handed one expands, the left transversal subspace contracts and the right one expands. Then we can say the left and right transversal subspaces have opposite quantum states of contracted or expanded at the same moment, but they have identical quantum states of contracted or expanded at opposite places in different consecutive moments (being identical because of their mirror symmetry and equal state, but distinguishable because of their opposite inner spin).
In this sense I consider the left contracted transversal subspace as a neutron that exists when at the right side there is an expanded transversal subspace that I consider an anti-neutrino. A moment later, when the left intersecting space expands and the right one contracts, the left contracted transversal neutron will decay getting expanded to form a neutrino while the right expanded transversal anti-neutrino will contract becoming a proton. Neutron and proton would not be two different quantum states of the same particle as Heisenberg suggested, but two opposite quantum states of two subspaces that have mirror symmetry between them at different consecutive moments, being at that moment Dirac antimatter.
The pushing force that takes place when the proton decays in an anti-neutrino will cause then the electron, and the directionally opposite pushing force that takes place when the neutron decays in a neutrino will generate the positron. And when the subspace passes through the orthogonal axis to be transformed from electron to positron or vice versa, a pulsating photon with a double opposite spin will be emitted.
These two transversal subspaces will be then fermions ruled by the PEP that must follow the Fermi Dirac statistics, although no probabilities are needed to calculate the position and state of the system and its nuclear subsystem as once we measure the state of a field and its subfield we can deduce the actual and next state and position of the other intersecting space and the others subspaces. I think the current probabilistic Copenhagen approach and its statistical interpretations comes because of considering an averaged wave function that englobates a composite system of at least two interrelated wave functions that form the shared subwave functions that constitute the electromagnetic nucleus of the system. (Without intersection won’t be subspaces, only more or less refracted emissions when the space contracts or expands).
When the phases of vibration of the intersecting spaces synchronize, the phase of vibration of the transversal subspaces are going to synchronize between them becoming symmetric (maybe the term «coherent» could be used here), but are going to desynchronize becoming antisymmetric (maybe the term «decoherent» could be used here), with respect to the two intersecting spaces.
So, if we measured the left intersecting space and its inner subspace and we got the state of being contracted, we could deduce the phases of vibration of the system are opposite, the right intersecting space is expanded, the right transversal subspace is expanded, and the orthogonal subspace is displaced toward left acting as an electron. But if we measured the left intersecting space is contracted and the left transversal subspace is expanded, then the right intersecting space will be necessarily contracted, the right intersecting subspace expanded, and the system will be emitting a photon. (I guess that by observing when the system emits a photon or by detecting an electron we could deduce its topological properties of the system and its evolution without directly interfering with it.)
So, with equal phase of vibration the left and right transversal subspaces are going to be mirror symmetric at the same moment, having the same quantum state of contracted or expanded. In this sense, they are not ruled by the Pauly exclusion principle and then they will be bosons following the Bose Einstein statistics.
Here, the two transversal subspaces would be then «entangled». I do not believe entanglement is possible in spatial separate particles although it’s being experimentally stated.
Notice that when the two intersecting spaces are expanded the pushing force caused by the descending side of the expanding spaces is going to create a compression in the transversal subspaces but only with one top down vector in each subspace. And the inner kinetic energy of that subspace is not going to be confined inside of the dual system because the vector pushing force that makes that confinement when the intersecting spaces contract has now an opposite direction. Maybe it could also be related to the mass gap problem because when it comes to opposite phases of vibration the energy and mass that the neutron losses when becoming a neutrino is going to be confined at the right side of the symmetry that has a space contracted at that moment.
Summarizing, the different states of the dual system would be these:
Thinking in terms of quarks as the forces of pressure caused by the intersecting fields while expanding or contracting, we can represent the mass gap in terms of lost forcesof prerssure inside of the concave side of the system in this way:
Part of the lost mass (and its related kinetic energy) would be explained by dark mass (and its related dark kinectic energy) taking place in the convex side of the dual system.
On the other hand, when it comes to opposite phases of vibrational spaces the transversal Schrodinger cat will be alive (contracted) at one side of the mirror and dead (expanded) at the other side at the same moment. But with equal phases of vibrational intersecting spaces the Schrodinger transversal cat will become transformed into a dog that will be alive or dead at both sides of the mirror at the same moment.
In both cases, the transversal subspaces will be extra dimensional, as additional spatial coordinates will be necessary to describe the subspaces. We cannot directly describe the transversal subspaces (or the orthogonal subspace moving in a pendular way) by means of the spatial coordinates of the intersecting spaces because the Z coordinate of the intersecting spaces, where the distances with respect to the fixed XY coordinates are a bit larger, is going to be coincident with the Y coordinate, where distances are smaller, inside of the frame of reference of a transversal subspace. It also happens between the referential coordinates of the stationary (with respect to the center of symmetry of the system) transversal subspaces and the displacing orthogonal subspace.
I think this context was the one which Herman Weyl originally considered when he initially thought about using a recalibration or gauge tool, that would let translate the metrics of the cuadrangular coordinates XY of the referential intersecting spaces to the rotated XY coordinates inside of the inner subspaces that are extra dimensional (because their rotated coordinates do not directly correspond to the coordinates of the spaces that formed them).
The moving subspaces reminds me of some of the figures Lobachevsky created to represent his imaginary geometry (ironically, having a perfectly consistent algebra his contemporaries did not understand him and he finally tried to draw visual figures to make them understand, without getting any result. It was necessary to still wait several decades).
I think the imaginary geometry, the intersection of parallels Lobachevsky algebraically developed, does not come from the curvature of the space as it was thought but by the rotation of the axes of coordinates that are in a different independent plane, in multidimensional manifolds (or extra dimensional subspaces):
The problem of different metrics and the effect of a contracted or dilated space depending on the different frame of reference also appears when it comes to tracing the diagonal inside of the referential square of area 1, when measuring the circle of the referential radius 1, or when comparing the perimeter with diameter of that circle. But no one seems to be trying to use different referential metrics and ideating a way to indirectly compare them through a shared calibration: the infinite decimals got «normalized» by means of artificially rounding the irrational (infinite) magnitude, creating an irrational constant, or by using «imaginary» numbers when it comes to the irrational diagonals.
When we have fixed XY coordinates, and without rotating both we trace a Z coordinate, for example inside of our referential square 1 (the referential metric we use to measure square and non square areas) we are not simply adding a new coordinate to that space, we are adding a new plane on the same space that is ruled by a different referential metric. Rotating that new plane from the static Y coordinate towards the Z diagonal we are creating the same effect as if we were expanding the space. And by rotating the Z coordinate towards X, we are creating the effect of contracting such space again.
The center of symmetry of squares 1 and 2 follow different and directly non comparable intervals. But if we repeat their rational and irrational intervals through the Z coordinate, we will find they periodically converge at the 5th and 7th intervals to form a complex zero. Using projections we can directly compare them without the result of getting infinite decimals in a linear limited segment:
If you are a static observer on the Y coordinate at the point it touches the blue outer circle, and I start to move – whatever my velocity is – towards the Z coordinate following the same circle towards right, we can think our frames or metric references are the same, the radius or the diameter of the circle, but they are actually not the same. If you preserve your fixed position your XY coordinates are fixed, by varying my position, the XY coordinates are going to rotate towards right, and what for me is going to be a Y coordinate, yo you is going to be a Z coordinate. The consequence is that for you the referential metric has become contracted.
We measure every distance with a referential straight segment, for example the segment of length 1, and we measure every area with a referential square, for example the square of area 1, built upon our referential segment. We do that not only for square areas but also for curved areas and then the problem of irrationality appears.
When we draw the diagonal inside of our referential square of area 1 we transform the referential segment for measuring distances making it larger. And we cannot compare those referential segments, the rational of the leg and the irrational of the hypothenuse directly without getting infinite decimals in a limited segment.
But if circle has the same radius in the X, Y, and Z coordinates, how can I say the referential metric has changed? Because we do not have a curved referential metric, we do straight referential metrics. Your referential frame related to the XY coordinates is the outer blue square of area 4 with rational legs and irrational hypothenuse, while my referential frame is the inner read square of are 2 with irrational legs and rational hypothenuse.
If you measure a distance being static in your position on the Y coordinate from the Y axes to the Z coordinate where the corner of the blue square is placed, that distance is going to be larger that the distance I will measure from the Y coordinate to the Z coordinate where the corner of the red square is located. You can say, yes, but the blue circle does not pass through the corner of the outer blue square, that corner will be related to a larger circle with a larger radius. Exactly, but remember that you do not have curved referential metrics, you only have straight segments for measuring distances and square areas for measuring spaces.
But if I keep moving from your Z coordinate (the rotated Y to me) towards your X coordinate, the consequence is that the referential metric is going to get expanded again. Our referential frames become the same.
And that happens periodically. The curvature of the circles looks for us perfectly symmetric, but in terms of our referential squares the actual circular figure is asymmetric:
That is why we get absurd results when trying to express in square or right linear terms the curved line that forms the perimeter when comparing it with the diameter.
That’s why the circle cannot be squared but in a projective way (which actually implies two – the outer and the inner – squares).
I think that apparently symmetric invariance that comes through the periodic expansions and contractions of the referential frames (or the frames of referential measures) is related with the Lorentz transformations that are in the base of special relativity.
I also think the gauge tool that Hermann Weil tried to introduced is also related to that, trying to introduce a bridge that lets compare different primary referential metrics without getting absurdly infinite or infinitesimal quantities (although when it comes to gauges I think they were considered for different spaces ruled by different referential metrics, as it’s the case of the mentioned transversal subspaces with respect to the orthogonal subspace and to the intersecting spaces, and I think the Lorentz transformations were thought about a same space what would imply a space that actually contracts and expands periodically or two different planes, one static and one rotational plane on a same space causing the effect of virtual expansion and contraction.
But coming back to the atomic system, we can consider this dual model as well as a topological vector space. Considering the vectors of the system as force carrier «particles» or «quarks», the model could be related to Quantum ChromoDynamics. But here quarks are not actual particles but simply the forces of pressure, the pushing forces created by the displacement of the intersecting spaces when contracting or expanding. These «quarks» are going to super symmetrically link the fermionic and bosonic subspaces by means of their periodical rotation:
I think the four quarks could be considered from the point of view of complex numbers, thinking in terms of 2 quaternions that form an octonion through time.
With respect to time, I think that to the 3 spatial dimensions of the intersecting spaces it’s necessary to add two time dimensions when it comes to fermions, one time dimension for each phase of vibration, that will converge in to one time dimension when it comes to bosons, and will diverge again later when the system evolves to fermions, and so on.
But what will cause the vibration of the interesting spaces? What will cause the periodical variation of their curvature? I think the only mechanical explanation is a force of pressure. There must be a flux in motion that passes through a dense distribution of something else finding a resistance in that dense distribution to be passed through, creating a wave diffraction of the flux that won’t pass through, and a refraction of the flux that passes through. Because of the friction, the density will become lower, changing the refraction of the wave and increasing its length, diminishing the refraction. I consider this thermodynamic mechanism gravitational. Gravity would be the force of pressure that creates the Einstein curvature, but the curvature will be periodically changing because the gravitational field itself would be a longitudinal wave. Einstein did not conceptually and mechanically explain why a density and a volume can curve a space, it mathematically described it. The idea of gravity as a pushing force was already proposed by Fatio, Le Sage and some others in different ways until the eather was discarded at the beginning of the XX century, but now it’s admitted the existence of a field that permeates the whole emptiness of the universe and whose vibrations, and any vibration implies a pushing force, are the Higgs bosons.
I think this model would be related to the De Broglie and Bohm wave pilot, as the fermionic subspace is driven or piloted by spatial displacements by two intersecting wave pilots that form it. And so, the model would also be related to the Everett many worlds because the system is formed by a plurality of worlds or universes that are formed by two intersecting (instead of parallel) worlds or universes.
Considering two intersecting spaces we can think about their shared subspaces as dependent on a «Common Cause Principle» to use the terminology used by Reichenbach in «The Direction of Time», (author I surprisingly I only recently discovered as I mentioned in a previous post), but when it comes to the electromagnetic nuclear atom there won’t be a common cause but two common causes.
In this same scenario we can also understand what is and why it happens the «collapse» of the wave function (the functions of the transversal subspaces describing fermionic behaviours when the phases of vibration of the intersecting spaces are opposite, start to describe bosonic behaviours when the phases of the intersecting spaces synchronize; and at that moment the function of the fermionic orthogonal subspace that was describing a pendular horizontal oscillation will start to describe a «fermionic» vertical oscillation).
I said «fermionic» vertical oscillation because that subspace does not have a mirror symmetric subspace with the same state at the same moment and at this sense it would not be ruled by the PEP when the phases are equal. In some cases in this blog I spoke about the ascending and descending subspace when the phases are equal as a boson because (although it would violate the PEP with respect its mirror subspace at the convex side) that subspace could be consider as the result of partially merging a left electron subspace and a right positron subspace that would converge at the same moment, having then the integral bosonic spin that results from -1/2 and +1/2. It could be imaginary described in that way if you will. But these labels are not so important when you understand the topology and evolution of the system. The labels are indispensably critical clues if you have no idea what is behind the statistical numbers you get from the Schrodinger equation.
In this sense maybe we could also think about the Pauli Exclusion Principle not in terms of mirror subspaces placed at the left and right sides of the centre of the symmetry of the dual system, but also in terms of mirror symmetric or antisymmetric quarks that are placed at the same moment in a same left or right side of the centre of the symmetry of the system. And in those terms the PEP works in a different way, because the mirror symmetric top and bottom quarks of the fermionic neutron – above and below a horizontal axes at the left side of the system – do not obey the PEP (in the terms of mirror symmetry we are interpreting it in this blog), they are mirror symmetric at the same moment. And the same can be said when a moment later they both simultaneously rotate 90 degrees when the neutron decays in a neutrino (when the left intersecting space expands and the right one contracts). When the phases become equal, by the contrary, the quarks of the transversal bosonic subspace in the left side of the system are not going to be mirror symmetric at the same moment, following the PEP, and in that case the double left and right quark of the orthogonal subspace are going to be mirror symmetric at the same moment not following the PEP.
But you know I do not think about quarks in terms of particles.
We can think in these terms also about macro spaces. Two intersecting universes getting contracted at the same moment will produce a photonic pushing force that can be interpreted as a big bang. But later, when they both expand, the big bang will be followed by a big silence (in the concave side of the dual universe system) and so on periodically.
Symmetries and asymmetries have been studied when it comes to atomic structures, but when it comes to the solar system there’s not a unique and mechanical explanation about them. The opposite rotation of Venus and other planets is being explained by ad hoc hypothesis, and the different eccentricities, inclinations, velocities and periodic fluctuations are considered as random casualties.
Do planets move by inertia or do they move because the field they orbit is getting contracted? Periodical variations of gravitational fields have not been detected but sometimes detections have come after predictions. Are all the planets of our solar system orbiting the same static and independent field? When Copernicus questioned the geocentric system he did it because he thought that model appeared to be a monstrous sculpture formed by the unrelated members of different creatures, that is to say, because of its unexplained asymmetries. Now, we have a system that is based on the same assumed type of space, a unique, independent and invariant space, the same that the geocentric one but with a different center, and we think we made a big revolution because the orbital center was changed.
Today Copernicus would question the heliocentric system as well. And maybe he would be able to arrive at the idea of a composite space. Ancient Greeks already thought about mirror matter speaking about Antichthon, the forgotten anti earth, and a central sun different from the visible one that implies a type composite system. I think the remaining revolution will pass for changing from the notion of a unique and or separate space with an orbited center to the idea of multiple, interrelated and composite subspaces manifolds that vibrate.
Topological quantum approaches are being used in quantum computation. One of them is the 2D called «anyons». Anyons are considered a quasiparticle that can indistinctly appear as a fermion or as a boson.
From my point of view anyons would be the spin of the intersecting longitudinal waves I described above. I found in Wikipedia an animation of 2D anyons that I see to be very similar to the mentioned spins and their evolution through the change of phases from fermions to bosons and vice versa:

By <a href=»//commons.wikimedia.org/wiki/User:Maschen» title=»User:Maschen»>Maschen</a> – <span class=»int-own-work» lang=»en»>Own work</span>, CC0, Link
I drew these next figures before knowing the existence of the model of anyons:
Finally I attache below a quite rudimentary animation I did some years ago to represent the motion of the system, although it does not represent the evolution through changing the phases, and it does not show either a rotational motion i think the whole system would have around its central axis.
(Between each expansion and contraction there will be a moment when there is no variation, if the space reaches its highest degree of expansion until it starts to get contracted again, that will cause a prelation (in a metaphorically similar way as oceanic tides get inverted through time).
Kind regards from Spain
Alfonso







 .
. 



 .
. 
 .
. 






 .
. 












Escribe tu comentario