Demostrando el quinto postulado de Euclides.

Desde que Euclides escribió los «Elementos» varios siglos antes de Cristo, en el que recogió todos el conocimiento matemático de entonces, se ha venido discutiendo mucho a cerca del postulado quinto conocido hoy como el postulado de las paralelas.

El postulado 5º afirma que: “Si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los ángulos menores que dos rectos”.

Mientras que los cuatro primeros postulados parecen hechos simples y evidentes, el quinto parece más bien un teorema que sería necesario demostrar, no puede aceptarse como un presupuesto de trabajo sin más. En ese sentido se ha dicho que Euclides trató sin éxito de hacer una demostración y ante la imposibilidad de lograrla, optó por incluir el teorema de las paralelas como postulado que habría que admitir sin demostración.

Muchos autores han tratado de probar la validez del quinto postulado sin éxito a lo largo de los siglos deduciéndolo de los cuatro primeros postulados o por medio de las proposiciones demostradas en los “Elementos”. Otros intentaron una formulación más sencilla del quinto postulado con el fin de facilitar su prueba. Entre estos últimos se encuentra el conocido axioma del escocés John Playfair según el cuál por un punto exterior a una recta no puede trazarse más de una paralela a dicha recta.

A comienzos del Siglo XIX Nicolai Lobachevsky demostró axiomáticamente que sobre un punto exterior a una recta puede trazarse más de una paralela si se considera como rectas las líneas trazadas sobre espacios curvos, dando así comienzo a la llamada geometría no euclidiana o hiperbólica, que es aquella que no sigue el quinto postulado de Euclides.

La geometría no euclidiana ha tenido en los dos últimos siglos un gran desarrollo y ha servido de base fundamental para el desarrollo de la física moderna. Por ello la demostración del quinto postulado de Euclides puede parecer hoy un tema ya superado, una mera curiosidad histórica.

Los cuatro primeros postulados se refieren al hecho de trazar una línea recta de un punto cualquiera a otro punto (postulado 1), prolongar continuamente una recta finita en línea recta (postulado 2), describir un círculo con cualquier centro y radio (postulado 3), y admitir que todos los ángulos rectos son iguales entre sí (postulado 4).

El postulado quinto habla de dos líneas rectas que no son paralelas. ¿Qué relación pueden tener con los cuatro postulados anteriores?

A mi modo de ver, el postulado quinto encaja lógicamente detrás del postulado cuarto porque el cuarto se refiere a dos ángulos – los ángulos rectos – que siendo iguales (teniendo los mismos grados) su suma es igual 180 grados, mientras que el postulado quinto se está refiriendo a ángulos – los ángulos internos del mismo lado – que siendo iguales o distintos distintos (teniendo diferentes grados) su suma es menor a 180 grados.

Cuando la suma de los dos ángulos internos del mismo lado es menor o mayor a 180 grados, sean esos ángulos iguales o distintos, las dos rectas no son paralelas y convergerán en el lado en que los ángulos son menores de 180 grados, divergiendo en el lado en que son mayores de 180 grados.

Pero ¿qué son los ángulos internos del mismo lado de los que habla el postulado quinto?

“Si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos”.

«Menores que dos rectos» significa que cada uno de los ángulos mide menos de 90 grados, o que la suma de los dos ángulos es menor de 180 grados.

Euclides se va a referir sólo a la convergencia en un punto de las dos líneas que no son paralelas, sin hacer mención a la divergencia de esas dos líneas, por eso no menciona los ángulos mayores de 180 grados.

Al decir “internos” Euclides parece estar refiriéndose al espacio interior formado por cada una de las dos rectas (paralelas o no) que formarían el borde o límite exterior de ese espacio. Y al hablar de “el mismo lado” se referirse al caso de que las dos rectas son cruzadas por una tercera línea que divide el espacio en dos lados, derecho e izquierdo.

De manera que si la suma de los dos ángulos que hay en el espacio interior formado por dos rectas, estando los dos ángulos en un mismo lado (izquierdo o derecho) de la línea que cruza a las otras dos, es menor de 180 grados, las dos rectas no serán paralelas y convergerán en algún punto situado en el lado en el que están esos dos ángulos.

Euclides no se refiere al caso de que las dos rectas se crucen una a la otra sin necesidad de estar atravesadas por una tercera, pero en ese caso la medición sería igual. Las dos líneas que no son paralelas pueden estar inclinadas hacia un lado o hacia otro, o pueden estar inclinadas hacia el mismo lado pero en distinto grado. En todo caso, las líneas solamente convergirán en el lado en el que la suma de los dos ángulos internos sea menor de 180 grados.

Entonces ¿qué se buscaba demostrar del postulado quinto? Habría que demostrar primero que cuando la suma de los dos ángulos internos es igual a 180 grados, las dos líneas son siempre paralelas; que cuando la suma de los dos ángulos internos es menor o mayor de 180 grados, las dos líneas no son paralelas; y que cuando las suma de los dos ángulos internos no es igual a 180 grados, en el lado en que los dos ángulos midan menos de 180 grados las dos líneas convergirán siempre en algún punto de ese lado divergiendo en el lado contrario.

Hay que tener en cuenta además la definición 23 de los “Elementos” que nos dice cuándo dos rectas se consideran paralelas: “Son rectas paralelas las que estando en el mismo plano y siendo prolongadas indefinidamente en ambos sentidos, no se encuentran una a otra en ninguno de ellos”. De manera que las líneas han de estar en el mismo plano.

También habría que ver cómo está relacionado el postulado quinto con las proposiciones del libro Primero de los Elementos que se refieren específicamente a las líneas paralelas, las proposiciones 27 a 31.

Una forma de abordar el problema de las no paralelas del postulado quinto, es partiendo de dos líneas paralelas cruzadas por una tercera. Podemos llamar a las dos líneas paralelas “a” y “b”. Si desplazamos una de ellas hacia el interior del espacio que forman, por ejemplo desplazamos “a”, haciéndola rotar desde un extremo, vemos que hay un punto en el que la recta desplazada “a” corta con la recta no desplazada “a”. Como la recta no desplazada “a” ahora ya no existe, podemos considerarla como una recta virtual y llamarla “va”. De manera que partimos de la existencia, aunque sea virtual, de un punto de convergencia inicial al que podemos llamar “vc”. El punto “vc” es el eje de rotación de “va” hacia “a”. Si hacemos rotar “a” lo suficiente, cortará en algún punto a la línea “b”. La suma de los dos ángulos internos formados en un mismo lado de la línea “a”, tiene que ser igual a 180 grados porque “va” y “b” son paralelas.

Podemos hacer lo mismo desplazando “b” hacia “b’” hasta llegar a cortar a “va”.

«va» y «vb» forman un paralelogramo virtual que no existe realmente en el momento actual porque las líneas ya han sido desplazadas hacia «a’» y «b’». Dentro de ese paralelogramo virtual hay un simetría de espejo entre derecha e izquierda y arriba y abajo.

Por la simetría de espejo, si existe un punto de convergencia inicial entre «va» y «a’», tiene que haber entonces un punto de convergencia entre «a’» y «vb». Del mismo modo, si existe una convergencia inicial entre «vb» y «b’», tiene que haber una convergencia final entre «b’» y «va».

Y si existen ambas convergencias, auqnue sean virtuales porque «va» y «vb» no existen en el momento en que existe «a’» y «b’», tiene que existir necesariamente una convergencia, una intersección real entre «a’» y «b’».

Podemos preguntarnos por qué han de ser paralelas las líneas cuando la suma de los ángulos internos es igual a 180 grados. Si trazamos una perpendicular que pase entre dos líneas paralelas, la suma de sus dos ángulos internos es 180 grados ya que los ángulos son rectos. Entonces lo mismo tiene que ocurrir si la línea que atraviesa dos paralelas tiene cualquier otra inclinación, las suma tiene que ser igual a 180 grados.

Un ángulo de 90 grados existe entre dos líneas perpendiculares la una de la otra. Es decir cuando los ángulos son de 90 o de 180 grados estamos trabajando con las coordenadas cuadrangulares X e Y. Pero cuando los ángulos no son 90, 180, 270, o 360 grados, hace aparición la irracionalidad, la inconmensurabilidad de toda diagonal Z con respecto a las magnitud racional de las coordenadas X e Y.

Los grados de una línea recta en las coordenadas X o Y es 180 grados, que es el arco de media circunferencia descrito por el radio cuando se desplaza de lado a lado en la coordenada X o en la Y.

Si desplazamos “va” 8situada virtualmente en la coordenada X) hacia “a’”, “a’” no se halla en las coordenadas racionales X o Y, se encuentra desplazada con respecto a ellas y su longitud será irracional, tendrá infinitos decimales siendo por tanto inconmensurable, hasta que la desplacemos hasta los 90 grados (con respecto a «va») haciéndola perpendicular con “va”. Si giramos “a’” otros 90 grados invertiremos su sentido con respecto a “va”, y así tendremos dos línea paralelas invertidas, “va” y “a’”.

Dos líneas sólo pueden ser paralelas si ambas están referenciadas a un mismo tipo de coordenadas, ya sean las coordenadas racionales XX o YY, o las irracionales, ZZ. Desde el momento en el que desplazamos una de las líneas paralelas, haciéndola rotar en cualquier grado con respecto a la coordenada en que se hallaba y no giramos en la misma proporción y dirección la otra línea, las dos líneas habrán dejado de ser paralelas.

Lo mismo ocurre cuando se desplaza Z en cualquier grado hacia un lado u otro, al desplazarla, estaremos creando una nueva coordenada Z+1º inconmensurable con respecto a Z-1º.

El problema fundamental que subyace en las no paralelas es el de la irracionalidad.

A mi modo de ver, cuando se desplazan una línea situada en las coordenadas X o Y que nos sirven de referencia y creamos la coordenada diagonal Z en un espacio plano bidimensional, lo que estamos haciendo sin darnos cuenta es transformar la magnitud que usamos como referencia para medir distancias lineales y áreas cuadradas en nuestro plano racional determinado por las coordenadas XY.

Así sucede cada vez que trazamos Z y queremos usarla con X e Y como si las tres coordenadas estuvieran en un mismo plano, el plano racional, aunque sabemos que, en él, las longitudes de Z nos resultan inconmensurables.

Lo mismo ocurre cada vez que desplazamos Z en cualquiera de los grados que van desde cero en Y hasta 90 en X, desde 90 en X hasta 180 en Y, desde 180 en Y hasta 270 en X, o desde 270 en X hasta 360 en Y.

El efecto de desplazar, haciéndolas rotar, las coordenadas intentando mantener al mismo tiempo las referencias racionales de X e Y, es decir, es el de crear un nuevo plano sobre el mismo espacio, el plano irracional. Y el efecto de trabajar con dos planos, uno de los cuales – el irracional – se desplaza mientras que el otro – el racional – está fijo, es el mismo que tendría lugar si el espacio sobre el que trabajamos se expandiera o se contrajera. De 0 a 45 grados el espacio se expandería, de 45 a 90 grados de desplazamiento el espacio se contraería, y así sucesivamente cada 45 grados. Es como tratar de medir un espacio fijo con un metro que se estira alargándose y se encoge contrayéndose periódicamente, o como querer medir con un metro de longitud fija en espacio que se expande y se contrae periódicamente. Este es el problema que está presente en la cuadratura del círculo en el que pretendemos medir con un cuadrado fijo situado en un plano de coordenadas racionales, un área circular en la que las coordenadas han rotado dando lugar a nuevos planos desplazados.

Para entender mejor lo que quiero decir podemos pensar cómo pudimos los seres humanos comenzar a medir distancias y áreas. Necesariamente hubo que comenzar por adoptar una longitud de referencia basada en la unidad, un pie, un codo, un brazo… al hacerlo, nadie midió cuántos puntos o líneas cabían en el interior del segmento aceptado como referencia, tácitamente se hizo la abstracción de pensar y asumir que el espacio dentro de ese segmento valía uno. Y que en adelante esa sería nuestra referencia para medir longitudes.

Sin embargo no se trata de una abstracción total porque en el centro de ese segmento de referencia hay un punto específico de división que determina su simetría y divide el segmento en dos partes iguales.

También hay dos partes iguales si colocamos a derecha e izquierda de un punto central un segmento de longitud 1 y llamamos segmento 2 a esos dos segmentos de longitud uno con su punto central.

Pero surge un problema con la proporción cuando queremos usar el segmento 1 y el segmento dos al medir una distancia: si colocamos el segmento 1 a la izquierda o derecha de un punto y al segmento 2 a la derecha o izquierda de ese punto, siempre habrá un segmento más largo que otro en uno de los lados.

Para solucionar este problema se puede crear un nuevo segmento de referencia al que llamamos segmento 3, formado por tres segmentos de longitud 1. Ahora podemos colocar en el centro un segmento 1 y a cada lado suyo otro segmento de longitud 1. La proporción se restablece y así podemos ya medir de 1 en 1, de 2 en 2, o de 3 en 3.

Y si la desproporción vuelve a surgir porque queremos usar el segmento 2 con el segmento 3, podemos crear otro nuevo segmento basado en la unidad que salve la desproporción que surge, y así creamos el segmento 5.

Lo que hacemos para salvar la desproporción cada vez que aparece es crear un nuevo número segmento primo.

Lo mismo cabe decir con la creación de los números diferentes de 1 y todos los números primos. los números no son entidades puramente abstractas, hacen referencia a cantidades y toda cantidad implica una distribución. En toda distribución hay una proporción y una simetría o un falta de ellas.

Ahora que podemos medir cualquier longitud rectilínea con nuestros segmentos de referencia basados en el segmento 1, podemos también intentar medir áreas. Primero áreas cuadradas. Pero para ello necesitaremos crear un área cuadrada de referencia basada en nuestro segmento 1, un cuadrado cuyo lado tenga la longitud 1.

De modo que construimos un cuadrado teniendo como lados nuestro segmento de referencia 1, y al espacio que queda en el interior le atribuimos el valor de 1. Ahora tenemos un área cuadrada que es nuestra referencia para medir áreas y que tiene el valor de 1. Y en su centro, hay un punto central que determina la simetría de su espacio interior, espacio cuyo valor numérico de 1 es una abstracción.

Ahora bien. Si trazamos una diagonal en el interior de nuestro cuadrado de referencia 1, surge de nuevo una desproporción. La diagonal de nuestro cuadrado 1 no puede medirse en base al segmento de referencia 1. Y en este caso no tenemos forma de salvar la desproporción en base a la unidad, porque la desproporción ha aparecido en la unidad misma. Es así como surge la irracionalidad, la inconmensurabilidad. La longitud irracional lo es porque no puede medirse en base a nuestra magnitud de referencia inicial.

Sin embargo comprobamos, como ocurre en el teorema de Pitágoras, que si construimos un cuadrado teniendo como lado la diagonal irracional de nuestro cuadrado 1, resulta que el área cuadrada que hemos construido mide lo mismo que dos de nuestros cuadrados de referencia 1. a^2 + b^2 = c^2.

Sin embargo también comprobamos que a^n+b^2 No es igual a c^n cuando n es mayor de 2.

¿Cómo se explica todo esto?

A mi modo de ver, los cuadrados a^2 y b^2 cuyos lados tienen longitud 1, no son iguales que el cuadrado c^2 cuyo lado tiene la longitud de la diagonal de a^2 o de b^2. Estos cuadrados son de naturaleza diferente porque su simetría interna y externa es diferente. Las áreas cuadradas y sus lados no son espacios o segmentos abstractos, tienen una simetría específica. Pero la simetría que siguen los lados de los cuadrados a y b (dada por el punto central del segmento de referencia 1) es coherente con la que tienen las dos diagonales del cuadrado c^2. Y la simetría de las diagonales de a^ y b^2 es coherente con la simetría de los lados del cuadrado c^2. Ello hace que en términos globales las simetrñias, aunque distribuidas de forma diferente, estén compensadas.

Así la suma de la longitud de los 8 lados de a^2 y b^2 es igual a la suma de las longitudes de las dos diagonales de c^2.

Y las cuatro diagonales de los cuadrados a^2 y b^2 tienen la misma longitud que la suma de los cuatro lados del cuadrado c^2. Es decir, las simetrías externas de a^2 y b^2 se corresponden con las simetría interna de c^2, y las simetrías internas de a^2 e corresponde con la simetría externa de c^2.

La irracionalidad también aparece cuando se compara el diámetro de la circunferencia con su perímetro. En este caso, la inconmensurabilidad surge en los infinitos decimales del número o magnitud irracional Pi.

A mi modo de ver la circunferencia es un área compleja en la que coexisten dos tipos de planos diferentes sobre un mismo espacio, el plano racional y el plano irracional.

Si dibujamos un cuadrado en el interior del circulo de radio 1, y otro cuadrado en el exterior del círculo, podemos ver que el cuadrado exterior toca con sus lados el círculo mientras que el cuadrado interior lo toca con sus esquinas. El cuadrado exterior es un cuadrado racional de área 4, mientras que el cuadrado interior es un cuadrado irracional de área 2. El cuadrado de área 2 es irracional porque su lado está construido sobre la diagonal de nuestro cuadrado de referencia 1 y por tanto es inconmensurable, no se puede medir sin obtener infinitos decimales.

Si dividimos el cuadrado de área 4 en cuatro cuadrados de área 1,y cada uno de estos en otros cuatro cuadrados de área 0,25, y luego dividimos el cuadrado de área 2 en cuatro cuadrados de área 0,50, si señalamos el punto central de cada uno de todos esos cuadrados y medimos a través de la diagonal Z la distancia que va desde el centro de la circunferencia hasta el centro de esos cuadrados, podemos ver que los cuadrados 0,25, 1 y 4 siguen el mismo intervalo repetido diferentes veces, mientras que los cuadrados 0,50 y dos siguen otro intervalo diferente. Estos son los intervalos de medición racional e irracional.

Pienso que estos intervalos vienen a ser lo mismo que lo que con sus propios términos Bernard Riemann “quanta” de múltiples variedades, y Hermann Weyl denominó gauges o diferentes escalas de distancia.

Pero si proyectamos estos dos intervalos diferentes a través de la diagonal de repitiéndolos uno detrás de otro de forma consecutiva, podremos ver que en un determinado intervalo, hay un punto de convergencia de los intervalos racional e irracional.

La convergencia en la recta diagonal de los dos tipos de intervalos parece un tema sugerente en el contexto de la convergencia de las paralelas.

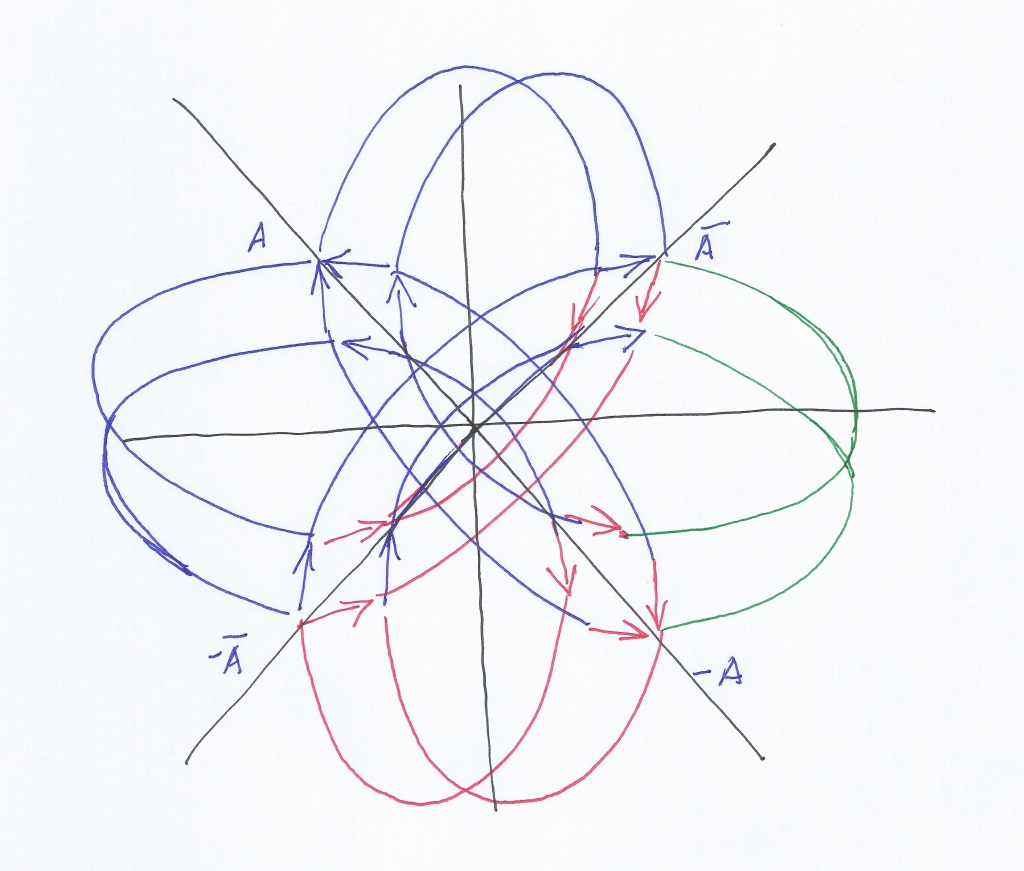
Los puntos de convergencia racional e irracional vienen a ser en mi opinión lo que Bernard Riemann llamó ceros no triviales al hablar de la periodicidad en la aparición de los números primos con su función Z.

En estos puntos que coinciden en el dibujo de abajo con el centro de las circunferencias representan un cero complejo en el que (al menos) las dos simetrías racional e irracional convergen. La convergencia ocurre de forma periódica.

Punto cero (convergen los puntos azul y rojo en el centro de la circunferencia)
1 punto azul (intervalo azul 1)
1 punto rojo (intervalo rojo 1)
2 punto azul (interval azul 2)
2 punto rojo (intervalo rojo 2)
3 punto azul (intervalo azul 3)
XXXXXX (No hay punto rojo)
4 punto azul (intervalo azul 4)
3 punto rojo (intervalo rojo 3)
5 punto azul (intervalo azul 5)
4 punto rojo (intervalo rojo 4)
6 punto azul (intervalo azul 6)
XXXXXX (No hay punto rojo)
Punto cero (Los puntos azul y rojo convergen al final del 7º intervalo azul y el 6º intervalo rojo).

Pienso que los intervalos comprendidos dentro de las dos filas marcadas con XXXX serían una representación de los que en términos musicales se conoce como «tritono», que es una parte de la escala musical que es considera disarmónica. Pienso que la diagonal es, de hecho, la representación de una escala musical.

En el caso del área de la circunferencia de radio 1, deberíamos poder medirla desplazando el cuadrado de área 1 a través de la diagonal siguiendo el intervalo racional hasta tocar la circunferencia con la esquina inferior izquierda del cuadrado 1, es decir, desplazando el cuadrado 1 tres veces.

Este triple desplazamiento que nos daría un área de valor 1+1+1 = 3, no es suficiente porque de ese modo sólo estamos teniendo en cuente la simetría del cuadrado interior del círculo, pero no la del cuadrado exterior. Para sumar la parte del área que falta, necesitamos desplazar el cuadrado 1 hasta el punto de la diagonal que representa a la simetría que falta. En el dibujo de abajo, el área que falta viene representada por la franja azul:

Y en el punto al que llega la franja azul, es justamente en el que se produce la convergencia entre los intervalos racional e irracional. De manera que no puede haber infinitos decimales en el área de la circunferencia porque la convergencia en ese punto hace posible la divisibilidad.

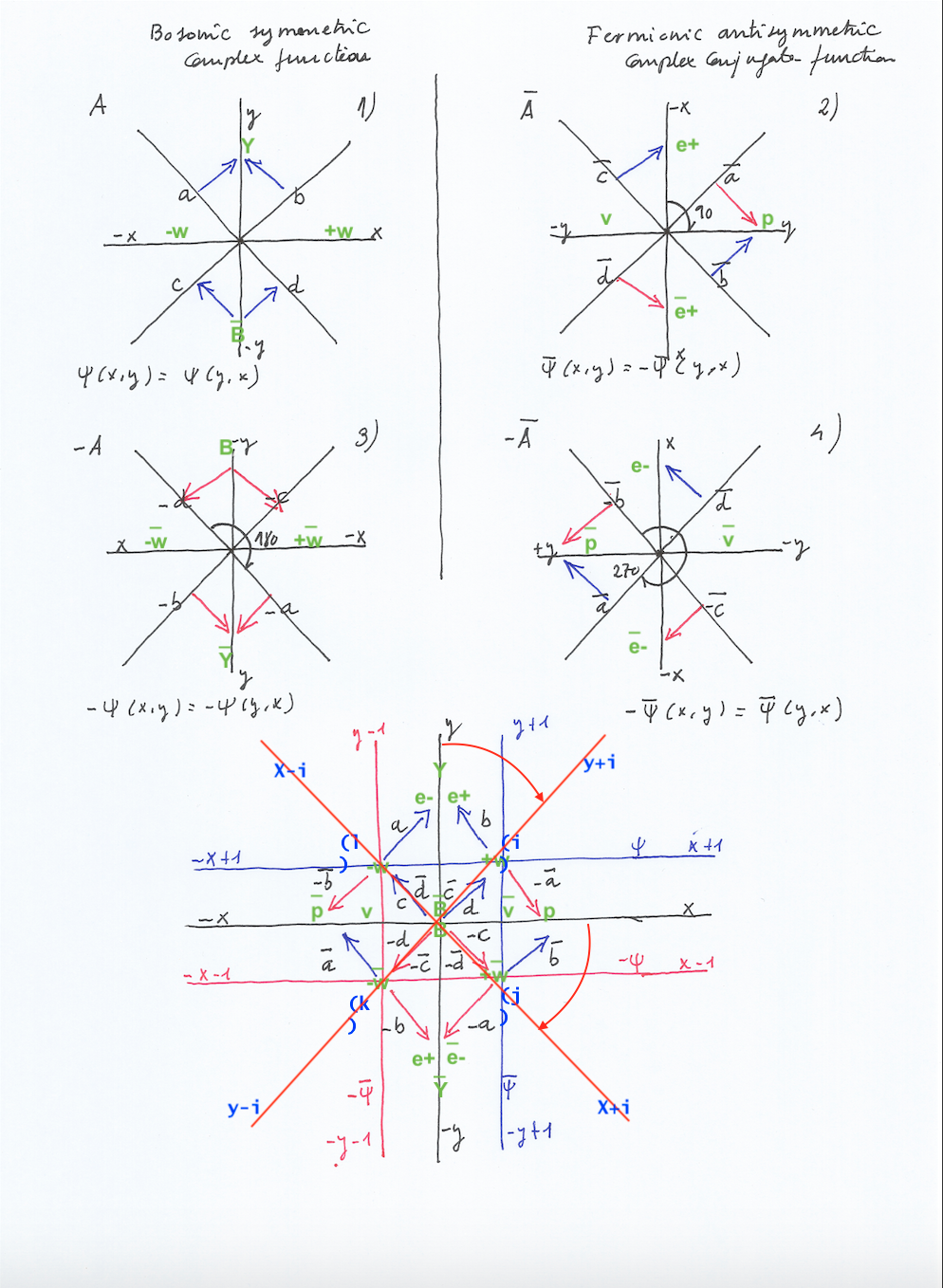
En el gráfico anterior se puede ver cómo los intervalos racional e irracional representados en sus extremos por puntos rojos y azules, siguen una secuencia inversa en las coordenadas X e Y comparadas con las coordenadas Z.

Un punto rojo en la coordenada X o Y corresponde en Z con un punto azul trazando una línea recta de unión perpendicular a X o Y. Esto parece indicar que no sólo los puntos ceros son puntos complejos sino que también lo es cualquier otro punto de cualquier coordenada en el que entonces concurrirán los dos tipos de simetría, formando las sucesivas coordenadas XY y Z un enrejado en el que se ensartan cada uno de los puntos del espacio.

Si cada uno de los puntos reales existentes en las coordenadas racionales XY están formado por la convergencia de dos líneas diagonales, una que viene de arriba hacia abajo (de derecha a izquierda, de fuera hacia dentro) y otra que viene abajo hacia arriba (de derecha a izquierda, de fuera hacia dentro), entonces ello implicaría no sólo que las dos diagonales cuando los ángulos internos del mismo lado son menores de 180 han de converger en un punto si no que además esa convergencia es la que da existencia y realidad a la línea racional de la coordenada X o de la coordenada Y. Algo así nos dice la ciencia óptica que ocurre en la visión, si no hubiera convergencia de ondas en un punto no veríamos nada en absoluto.

En definitiva. En mi opinión, cuando dos líneas no tienen el mismo grado y dirección de inclinación referenciado a un mismo tipo de coordenada, X, Y, o Z+n, no son paralelas. En el caso en que la suma de los ángulos internos del mismo lado no sea igual a 180 grados existirán dos tipos de planos diferentes en el mismo espacio, inconmensurables uno con respecto al otro, lo que queda fuera de la definición de paralelas de Euclides como rectas existentes en el mismo plano.

Euclides habla de rectas que se prolongan indefinidamente, con lo que puede pensarse en rectas infinitas en un espacio infinito. Cómo podemos saber con seguridad que las rectas inclinadas más allá o más acá de 180 grados exactos convergerán en algún punto de ese infinito espacio? Si las rectas están inclinadas. lo están con respecto a nuestro eje de coordenadas de referencia X o Y sobre las que construimos nuestro cuadrado de referencia 1. De manera que el paralelogramo virtual o semivirtual existirá siempre, porque la diagonal siempre estará desplazada con respecto a X o Y. De manera que el espacio estará delimitado en cualquier caso por esas coordenadas virtuales que hacen de límite; aunque uno de los dos lados no tengan límite – porque si el espacio fuera infinito no podríamos no podríamos trazar una perpendicular al final – sí que podemos trazarla al inicio en el eje de rotación de la diagonal; La línea diagonal no pude prolongarse entonces hasta el infinito sin converger en algún punto con la recta virtual o no virtual del paralelogramo con el que hemos limitado el espacio, coherente con nuestras coordenadas racionales X e Y.

Respeto a las geometrías no euclidianas, me da la impresión de que lo son porque no siguen la definición de paralelas de Euclides ya que trabajan sobre espacios que varían o sobre espacios espacios fijos en los que se se combinan diferentes planos, unos de ellos irracional desplazado con respecto al otro racional.

Más adelante añadiré al post la relación del postulado quinto con las proposiciones 27 a 31 de los Elementos y alguna bibliografía para quienes estén interesados en este tema de las paralelas y no paralelas.

Otro tema que surge de lo dicho anteriormente es el de si existen varios tipos de paralelas. Las paralelas de Euclides lo son porque no convergen nunca (cuando la suma de los dos ángulos internos de un mismo lado es igual a 180 grados). Podemos pensar que esas líneas de Euclides que se prolongan indefinidamente están hechas poniendo uno detrás de otro nuestro segmento segmento de referencia. Aquí da igual que el segmento que usamos en una de las rectas sea inconmensurable con respecto al otro, los dos convergerán en un punto al interseccionarse.

Pero qué ocurre si usamos dos segmentos de referencia métrica, dos gauges inconmensurables entre sí, el segmento de referencia racional y el irracional, y en lugar de formar con ellos dos líneas separadas, los ponemos uno encima del otro (o uno proyectado a distancia sobre el otro. Aquí, el punto de convergencia en el caso en que la terminación, el extremo, de cada uno de los dos segmentos concurriese en algún momento en un punto; Mientras que no converjan, esas dos líneas serán paralelas. De manera que aquí el «paralelismo» (o la cualidad de ser paralelas las rectas) viene dado por la existencia de dos líneas regidas por segmentos de referencia métrica, por gauges, diferentes e inconmensurables entre sí, el racional y el irracional; mientras que en las paralelas de Euclides, el «paralelismo» viene dado porque ambas rectas están regidas por segmentos de referencia de la misma naturaleza, la racional, la regida por las coordenadas XX o YY, (o irracional regidas por las mismas coordenadas Z+n Z+n).

Ya que una de esas líneas es irracional con respecto a la otra, siguiendo la matemática actual ambas serían siempre paralelas porque no convergerían nunca. Es lo que ocurre cuando obtenemos infinitos decimales en las magnitudes irracionales. Nunca obtenemos un número entero que ponga fin a la infinita división, el número enteros representaría la convergencia de las dos rectas. Pero según las figuras puestas anteriormente, los dos intervalos convergen periódicamente.

Desde el Siglo XIX la matemática ha sufrido (y quiero decir literalmente sufrido, no ya experimentado) un proceso de extrema formalización hasta llegar a un punto en que la geometría descriptiva, la que se representa con figuras geométricas, ha dejado de ser considerada verdadera matemática y se entiende como si fueran dibujos que carecen de valor probatorio. El fin, como decía Poincare comentando el libro de fundamentos de la geometría de Hilbert es hacer una formalización tal que cualquier persona, sin saber lo que es un punto o una recta, sea capaz de hacer un desarrollo geométrico operando maquinalmente con las herramientas de la geometría formalizada, es decir, los axiomas, el álgebra, las ecuaciones, la aritmética.

El nivel de abstracción ha llegado a tal extremo que se han hecho desarrollos matemáticos que no se sabe a qué corresponderían en la realidad, no se tiene ninguna referencia visual de ellos, y el problema viene cuando se llega a un punto de estancamiento en el que no hay referencias. Tal como les ocurre a los físicos atómicos actualmente. Porque toda la física del Siglo XX se ha hecho sobre la base de desarrollos matemáticos abstractos.

Este exceso, yo diría que patológico de formalización y abstracción ha tenido una enorme influencia en la forma en que las matemáticas han sido enseñadas en las escuelas y el rechazo instintivo que hacia ellas han tenido todas las personas que las han sentido como algo extraño e ininteligible, las personas que se han dedicado a humanidades o arte porque las ciencias les producían un rechazo total debido a su matematización y a la algebraicización y aritmetización de las matemáticas.

En la antigua Grecia, las matemáticas eran fundamentalmente geometría, eran un conocimiento predominantemente visual sobre el que se podía pensar. En el frontispicio de la Academia de Platón estaba grabado un texto en el que se negaba el paso a todo aquél que no supiera geometría. La mayoría de los matemáticos de hoy no tendrían acceso a la Academia. No entienden las figuras geométricas. Las ven como si fueran dibujos ajenos a la verdadera matemática que es el álgebra y la aritmética. Hoy no se piensa ya en los fundamentos, se opera, se calcula, se combina maquinalmente.

Como todos los excesos, el formalismo ciego y fundamentalista de la matemática actual pasará y se verán los excesos cometidos. Pienso que antes o después se verá que si la intuición de la geometría descriptiva, lo mismo que el sentido común, pudo dar lugar y dio lugar históricamente a conclusiones equívocas, también la aritmética y el álgebra aplicado sin sentido, no supeditado a la razón, ha conducido a resultados incorrectos, siendo para mí el más evidente el de la falta de comprensión de la irracionalidad y las consecuencias que se han derivado de ello.

La geometría no euclidiana o hiperbólica, que no sigue el quinto postulado de Euclides al admitir que sobre un punto exterior a una recta puede trazarse más de una paralela a esa recta, fue iniciada por Nicolai Lobachevski (también se puede encontrar escrito como Lobachevski, Lobachevskii, o Lobachevskij). Lobachevski se planteó la posibilidad de que el postulado de Euclides fuera no verdadero, y comenzó a desarrollarla de una forma axiomática, sin ninguna referencia geométrica ni nada visual a lo que agarrase, y en contra de la intuición que parece mostrar que no cabe más que una paralela en relación a otra línea. Y a medida que iba desarrollando su hipótesis fue viendo que era perfectamente consistente en sí misma y con el resto de los postulados de Euclides excepto el de las paralelas.

Por la falta de referencias con el mundo real, el que hasta entonces había sido descrito geométricamente con los Elementos de Euclides, Lobachesvki llamó a su geometría «imaginaria».

La geometría no euclidiana que se considera hoy, no es propiamente la geometría de Lobachevsky, es la geometría no euclidiana pasada por el filtro de los modelos y representaciones que otros autores hicieron con posterioridad como la esfera de Riemann y otras.

Para entender la geometría de Lobachevski hay que ir a su obra original. Hay poca bibliografía de Lobachevski en inglés, no digamos en español, y así de sus libros sólo están publicado los dos últimos: «Geometrical researches on the theory of parallels» («Investigaciones geométricas sobre la teoría de las paralelas») publicado en 1840 y traducido en 1914 por Halsted (este es un libro de sólo 45 páginas en el que Lobachevsiki hace un resumen de sus ideas y muestra algunas figuras geométricas haciendo más inteligible e intuitiva su geometría); Y «Pangeometría» que es su último libro.

En este dibujo de su libro «Investigaciones geométricas» muestra una aproximación de lo que para él serían varias paralelas pasando por un punto exterior a una recta. La recta, como se ve, no es una linea recta si no que es una curva. A mi me parece que el uso de la línea curva como recta, basándose en que los Elementos de Euclides no definen claramente qué es una recta, es claramente forzado y da la impresión que lo usó como la única forma que pudo de representar su geometría no euclidiana en términos euclidianos.

Lo que se aprecia en el dibujo de Lobachevski, a mi modo de ver, es que las dos líneas que el considera dos paralelas (paralelas con respecto a la curva) pasando por un mismo punto, es es realidad un misma paralela que oscila de forma pendular, es decir, se trata de una misma paralela pero vista en dos momentos diferentes.

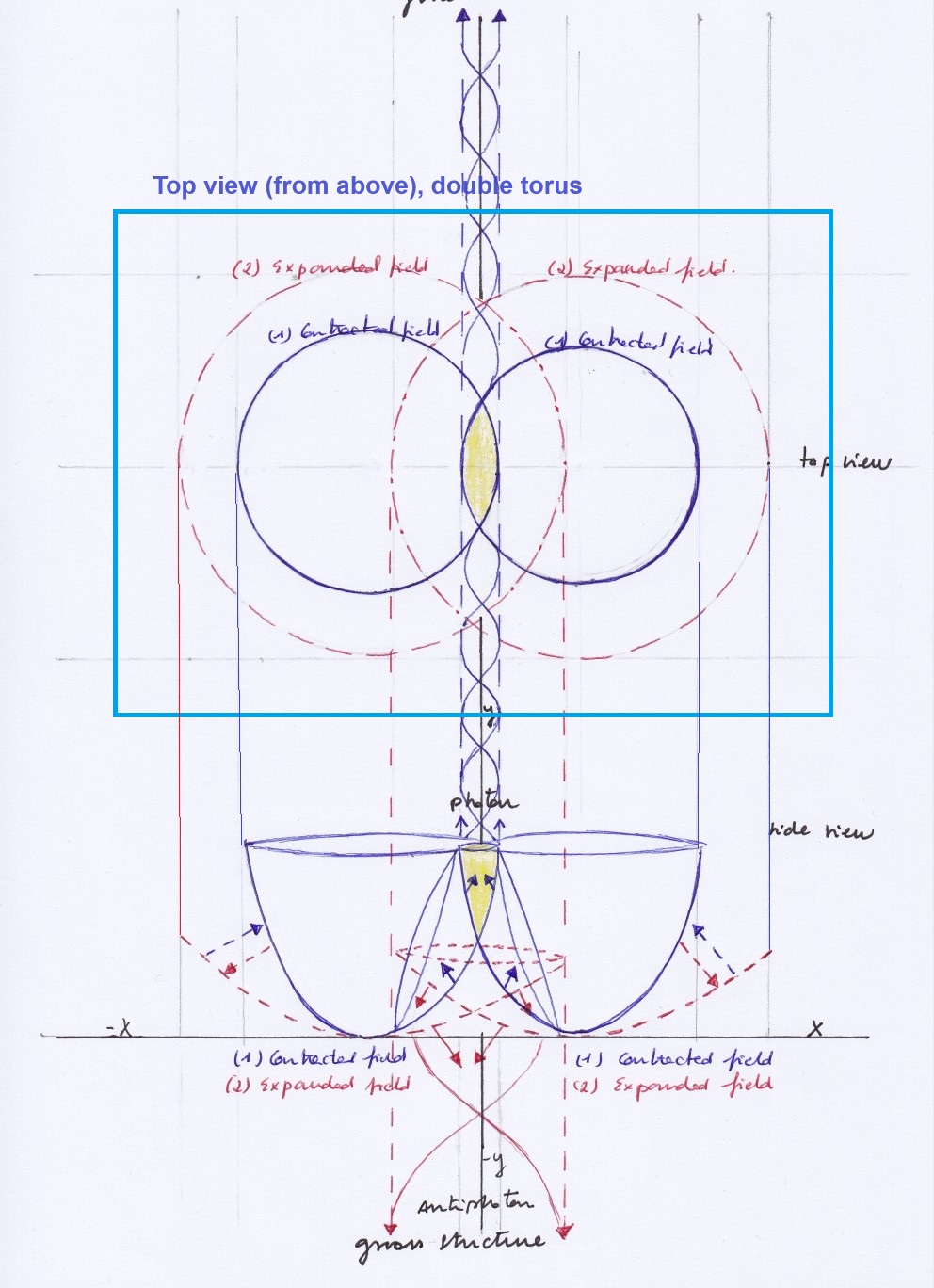
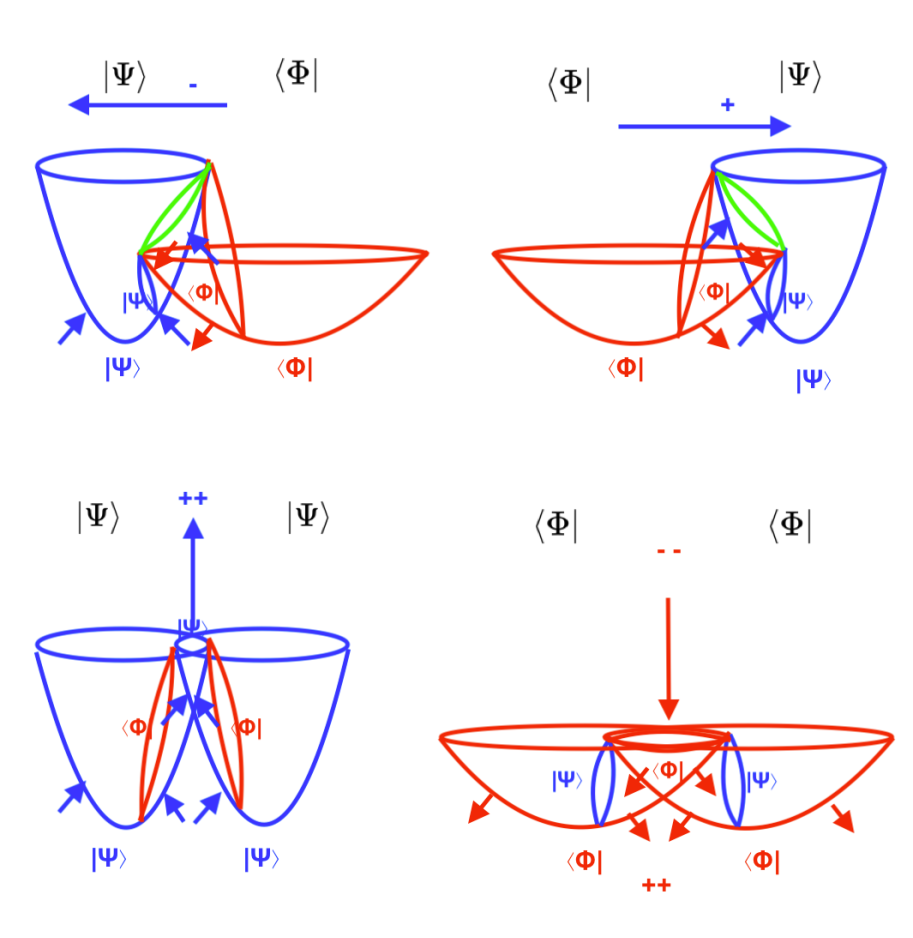
Cuando define los axiomas de los que parte en su geometría, Lobachevsky menciona en sus «Investigaciones geométricas» la intersección de dos esferas; también habla de que su geometría es una interacción de espacios, y de que es bidimensional.

Todo ello se entiende mejor a mi modo de ver, representando la intersección de dos esferas.

Y más claramente, representando la intersección de dos semiesferas o dos campos cóncavos, dos ondas longitudinales, que se expanden y se contraen periódicamente, con la misma fase (es decir que ambas se expanden al mismo tiempo y luego ambas se contraen), o con fase opuesta (es decir, que cuando una se expande la otra se contrae).

Cuando ambas varían con la misma fase, el punto de intersección entre ambas asciende y desciende de forma vertical; cuando varían con fase opuesta el punto de intersección se desplaza de izquierda a derecha.

Lobachevskij pensaba que su geometría imaginaria, pese a no encontrar un modelo, una representación para ella, era lo que regía la naturaleza.

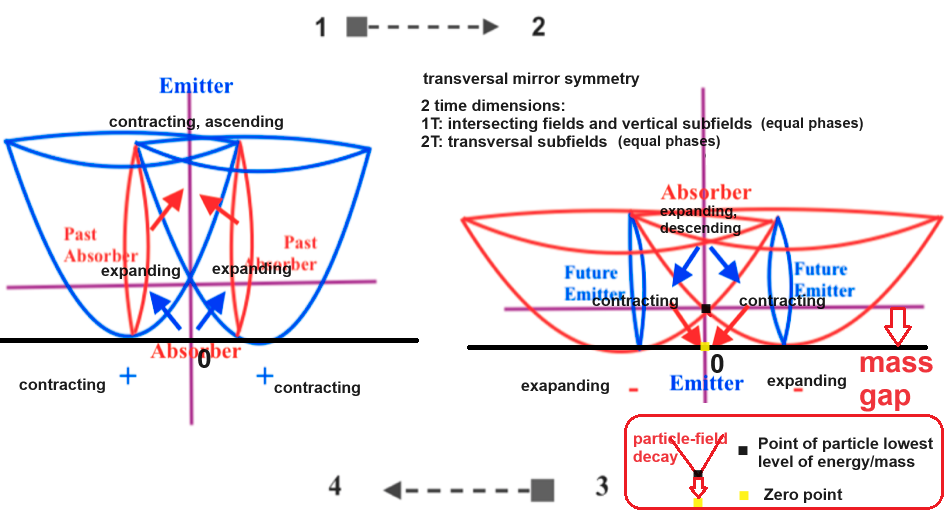
Cuando los campos intersectados varían al mismo tiempo, cuando se contraen y hasta llegar al punto máximo de contracción las dos líneas verticales no son paralelas (dibujadas en rojo en la figura de arriba). Cuando dese el punto de máxima contracción los campos comienzan a expandirse, ocurre lo mismo, las líneas verticales no son paralelas hasta que llega un momento en que las líneas verticales se hacen paralelas; pero es sólo un momento, una frontera entre las no paralelas positivas y las negativas, porque a partir de ahí, al seguir expandiéndose los campos las líneas verticales vuelven a hacerse no paralelas.

Las paralelas de Lobachevski no son líneas curvas, son líneas rectas que surgen de un modelo curvilíneo que varía periódicamente.

En esta otra imagen los campos varían con fases opuestas y aquí ocurre lo contrario, las líneas verticales son siempre paralelas hasta llegar a un punto en que se hacen no paralelas, es el punto que marca la distinción entre negativo (cuando el campo izquierdo se contrae produciendo un desplazamiento hacia la izquierda), y lo positivo, cuando el campo derecho se contrae, expandiéndose el izquierdo, produciendo un desplazamiento hacia la derecha.

Mientras que la primera figura, con fases iguales, la frontera entre lo negativo y lo positivo viene marcada por un momento o iuna franja de momentos de paralelismo, en la segunda figura, con fases opuestas, la frontera entre lo positivo y lo negativo viene marcada por un momento o una franja de momentos de no paralelismo.

La primera figura representa dos campos intersectados que varían al mismo tiempo, de manera que cuando ambos se contraen, todas las líneas horizontales son paralelas, mienstras que las verticales convergen en un punto.

La segunda y tercera figura muestran cuando los dos campos intersectados varían con fases diferentes; aquí ocurre lo contrario, las líneas verticales son paralelas, mientras que las horizontales convergen.

A medida que los campos se expanden y se contraen, y se produce el desplazamiento ascendente y descendente o de izquierda a derecha, se van generando diferentes líneas que son las distintas paralelas de la geometría de Lobachevsky que pasan por un mismo punto que se desplaza.

Este modelo no lo hice para representarla geometría de Lobachevski, lo hice para representar un núcleo atómico y un sistema solar formado por campos entrelazados que varían periódicamente. Lo hice partiendo de la idea de que los campos de gravedad varían periódicamente, que aunque no se haya comprobado todavía, se expenden y se contraen.

No es posible sin embargo discutir con ningún físico sobre este modelo atómico ni con ningún matemático sobre las figuras geométricas porque no las entienden. Es más, las figuras geométricas son vistas como algo que no son matemáticas, carente de interés. Y no las entienden porque, siendo tan simples, no las han visto antes nunca, lo que es bastante patético. El modelo atómico actual se desarrolló sobre la base de una geometría no euclidiana carente de una representación clara.

Considerar a una curva como recta es una ficción, es una solución forzada e irracional que se hace necesaria, de forma instrumental por no darse cuenta de que aunque los modelos no euclidianos son curvos, las rectas paralelas o no no son curvas, son propiamente rectas en el sentido euclidiano. A partir de ahí, de ese no darse cuenta, se ha ido forzando todo lo demás de forma instrumental sobre la base de una abstracción total basada en una aritmética y sostenida algebraicamente. No hay una representación visual del modelo de átomo actual, hay sólo una estructura matemático algebraica que la sostiene a base de aceptar inconsistencias lógicas.

A día de hoy la física está atascada porque los modelos que se han desarrollado son insuficientes y no se tiene ninguna referencia lógico-racional ni visual que puedan dar una idea de por dónde seguir.

Y para mi, el problema de no saber por dónde seguir implica que no se puedan entender los mecanismos últimos que rigen la división celular ni sus anomalías o que no se sepa todavía cómo controlar la gravedad sin gastar energía o transformar la materia sin destruirla.