Abstract: A composite topological atomic model of intersecting curved spaces and subspaces that vibrate with same or opposite phases would provide visual insight about the physical mechanism underlying the «handshake» transactions of the subatomic quantum states that occur in the strong and weak interactions between a retarded wave that evolves forward in time and its advanced complex conjugate that evolves backward in time, clarifying the notion of time reverse or anti-time considered by the «Two state quantum formalism», the Wheeler-Feynman «Absorber theory», or the «Transactional» or the «Two Time» interpretations of Quantum Mechanics, making sense of the concepts and paradoxes of quantum mechanics in a logical way.
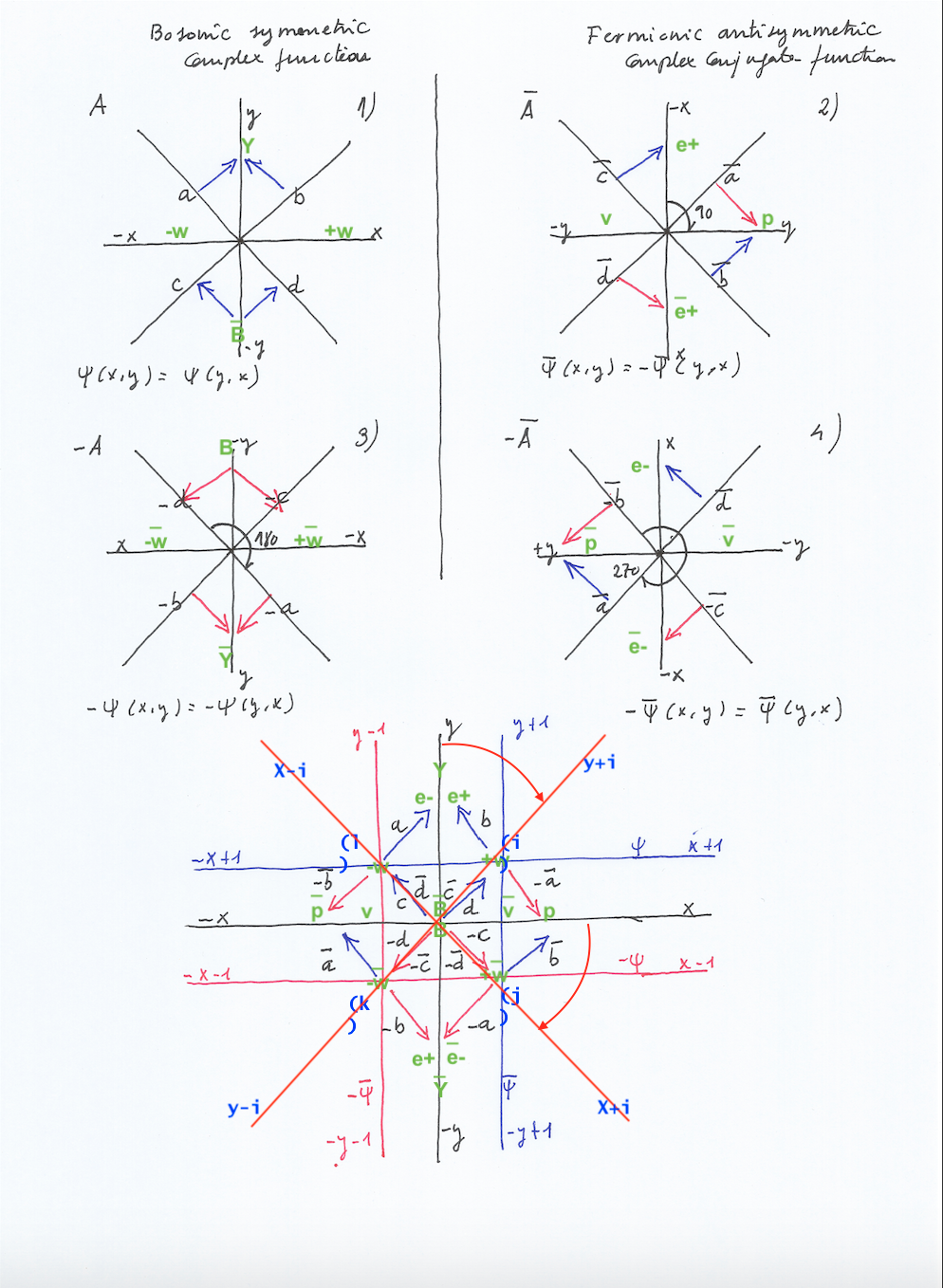
The two-state vector formalism is a description of quantum mechanics in terms of a causal relation in which the present is caused by quantum states of the past and of the future taken in combination. (1)
Initially developed by Satosi Watanabe in 1955, it’s one example of a time-symmetric interpretation of quantum mechanics. It proposes that the information given by forwards evolving quantum states is not complete; rather, both forwards and backwards evolving quantum states are required to describe a quantum state: a first state vector that evolves from the initial conditions towards the future, and a second state vector that evolves backwards in time from future boundary conditions. Past and future measurements, taken together, provide complete information about a quantum system.
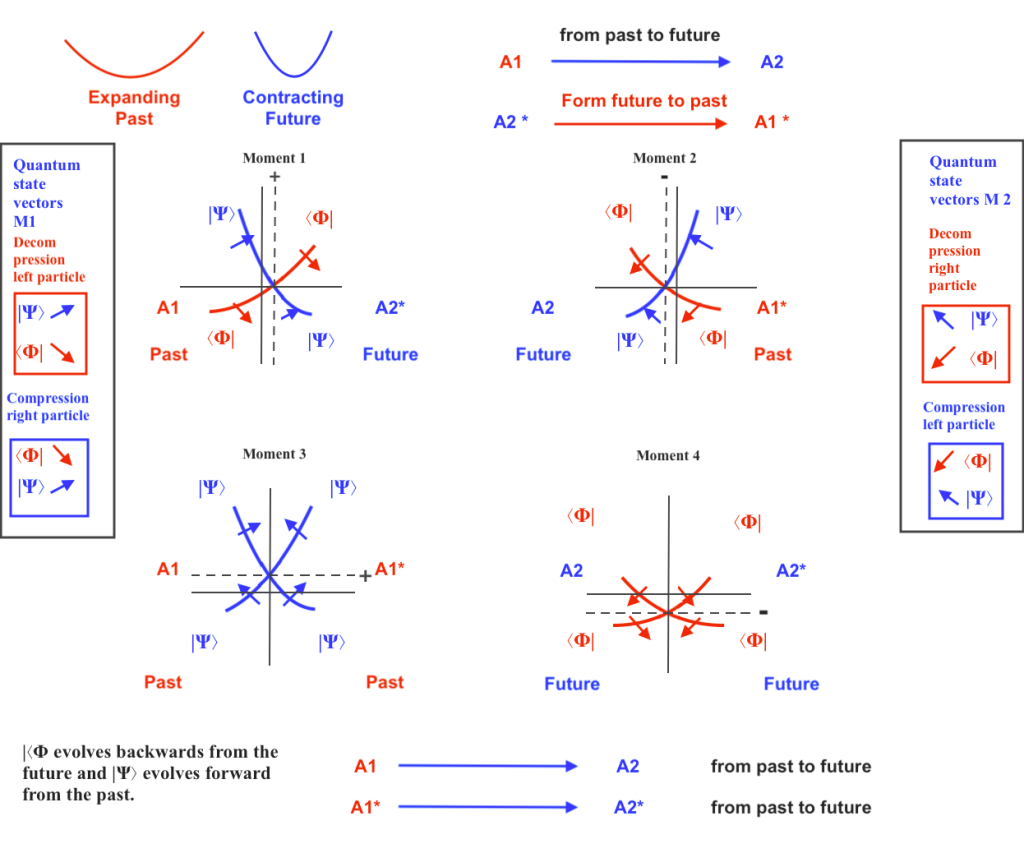
The two-state vector is represented by ⟨Φ| |Ψ⟩, where the state ⟨Φ| evolves backwards from the future and the state |Ψ⟩ evolves forward from the past.
So, according to the TSVF interpretation, a present quantum state will be caused by a combination of a past cause (a forward causation) and a future cause (a backward causation or retrocausality).
The two-state vector formalism has similarities with the transactional interpretation of quantum mechanics that proposed by John Cramer in 1986, taking inspiration from the Wheeler-Feynman Time-symmetric theory or absorber theory (also known as direct action theory).
The transactional interpretation of quantum mechanics takes the wave function of the standard quantum formalism and its complex conjugate, to be retarded (forward in time) and advanced (backward in time) waves that form a quantum interaction as a Wheeler–Feynman «handshake» or transaction. (2)
According to the transactional interpretation, a source emits a usual (retarded) wave forward in time, but it also emits an advanced wave backward in time; furthermore, the receiver, who is later in time, also emits an advanced wave backward in time and a retarded wave forward in time. A quantum event occurs when a «handshake» exchange of advanced and retarded waves triggers the formation of a transaction in which energy, momentum, angular momentum, etc. are transferred.
The transactional interpretation of Quantum Mechanics (TIQM) proposes that a transactional interchange occurs between the Schrodinger wave function Ψ moving forwards in time (from past to future), the so-called retarded wave, and its mirror symmetric complex conjugate wave function Ψ* moving backwards in time (from future to past), the so-called advanced wave. As a commercial agreement closed by a handshake, the forward and backward waves will interchange energy, momentum, etc when meeting at a present time.
The TIQM lets making sense of some illogical paradoxes of quantum mechanics that have not been solved by the Standard model or its different interpretations; but the mechanism of the «handshaking» that closes the transaction between the wave and its complex conjugate remains something abstract, and it also presents the apparently unreasonable assumption that the advanced complex conjugate wave can travel backwards in time, from future to past.
On this article it’s suggested that a dual composite atomic model of intersecting longitudinal waves would clarify the handshaking transactional mechanism not only between particles of two different atoms but also between the particles of a same atomic nucleus, describing the evolution of the quantum states of those subatomic particles and the supersymmetric link between bosons and fermions. In this context, retrocausation and time reverse waves can be rationally understood.
Initially it seems logical to state that any present or future event only can be the effect of a past cause, because time always goes from past to future. So, a present event could never be the effect of a cause that comes from future to past. But lest go to put this terminology into context.
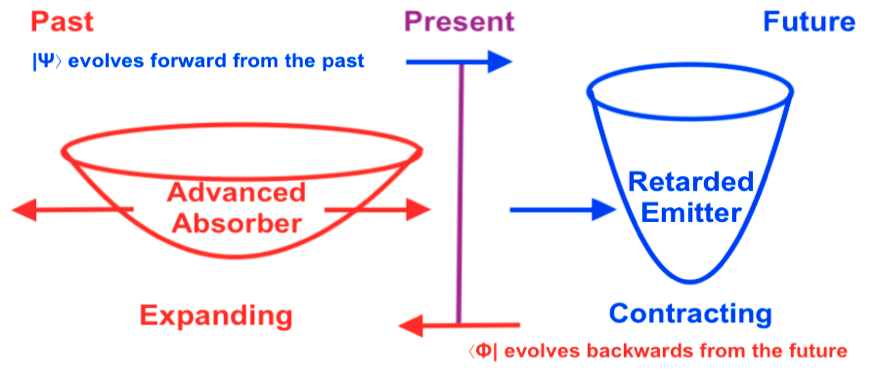
Thinking about a longitudinal wave that vibrates, we can consider the state of being expanding as a quantum past event and the state of being contracting as a quantum future event. The highest degree of expansion or contraction will be the time boundaries of the system.
As it’s a cyclical system, the past state of being expanding will evolve forward to the future state of been contracting, and the future state of being contracting will evolve backward to the past state of being expanding. At a present moment the wave quantum will be an intermediate combination of the retarded past and the advanced future states.

The physical properties, (increased or decreased inner kinetic energy, volume and density, or implied pushing forces), of each quantum state of being expanding or contracting can be considered as a consequence of a transactional exchange completed through time between those quantum states of the same vibrating wave.
So, for example, the decreasing inner kinetic energy of the past expanding sate will be inversely equivalent to the increasing inner kinetic energy of its future contracting state. Expressing this interchange with the TIQM it can be said, surely in a kind of free way as I’m not speaking about traveling emitted or received waves but about evolving quantum states of a same wave, that the past expanding wave will act as the retarded absorber handshaking with the future contracting wave acting as the advanced emitter.
Retrocausality and time reverse travel cannot be understood as a pure mathematical abstraction separated from space. Time is the measure of the variation that occurs in a static or varying space, or the variation of a varying space itself.
But a single invariable space orbited around its centre, a sort of heliocentric model, cannot explain the atomic electromagnetic properties and behaviours. A single vibrating space orbited around its centre, neither.
But time can also be the measure of the variations related to a composite space or «manifold» of spaces and subspaces that may not be possible described with only three spatial coordinates and a single time coordinate, a multidimensional composite and vibrating space.
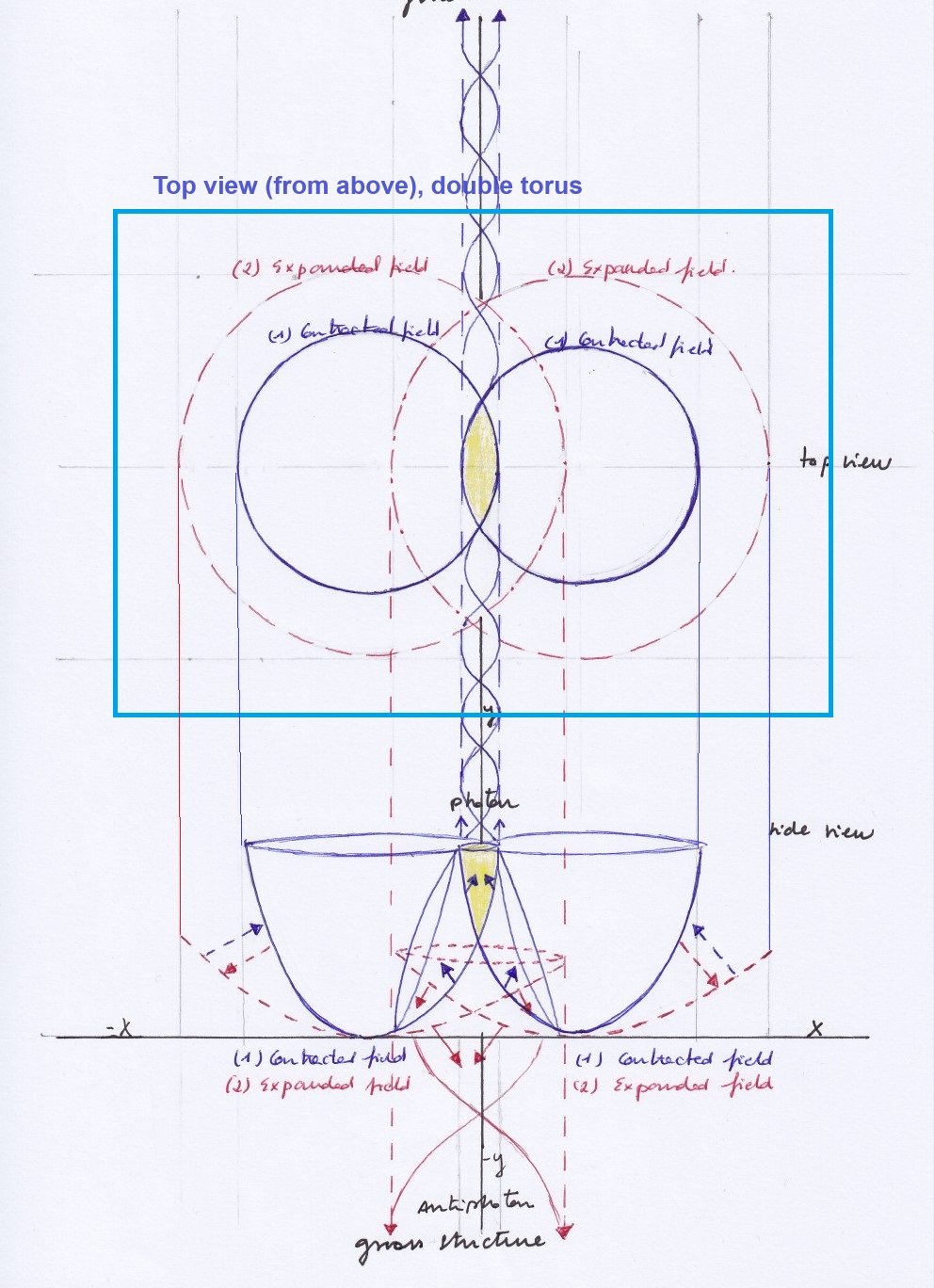
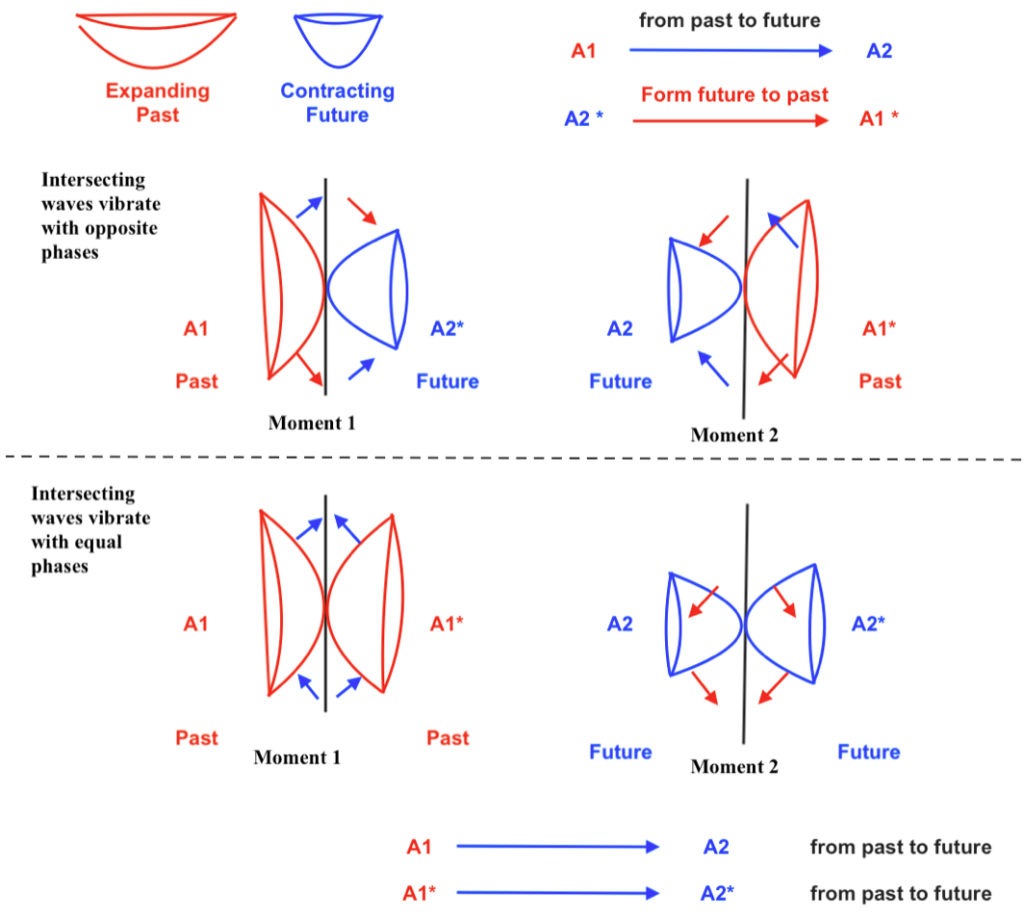
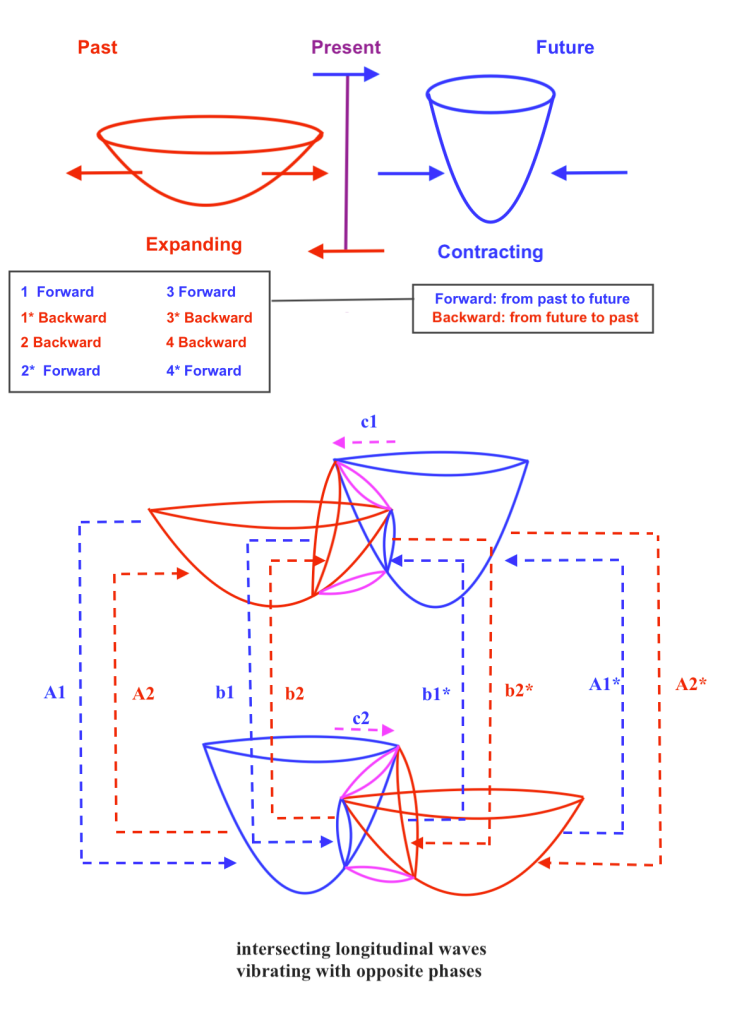
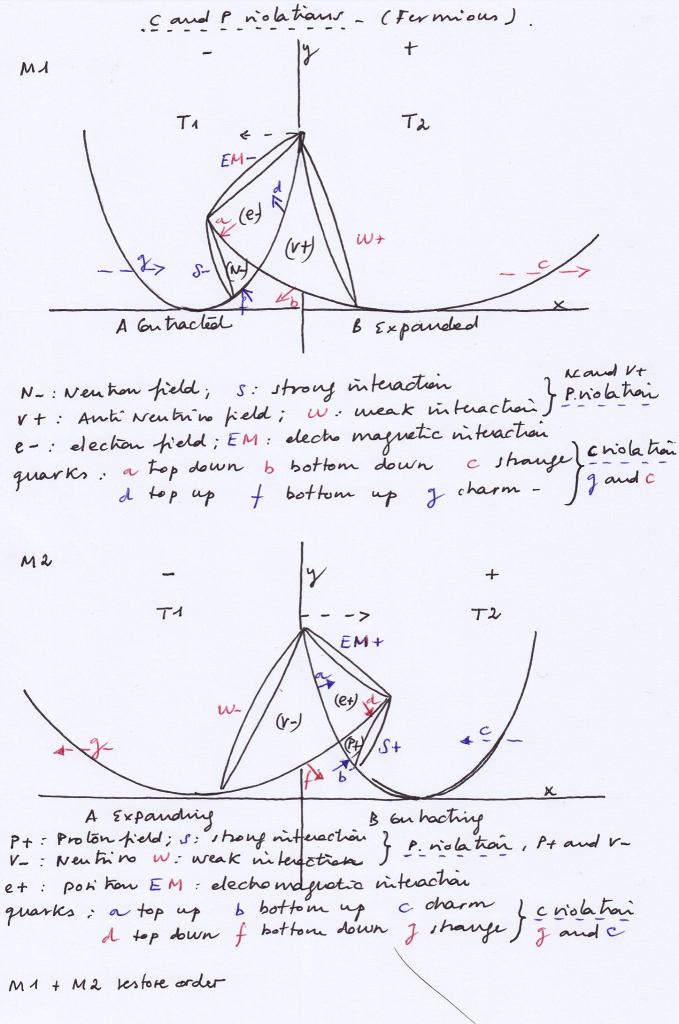
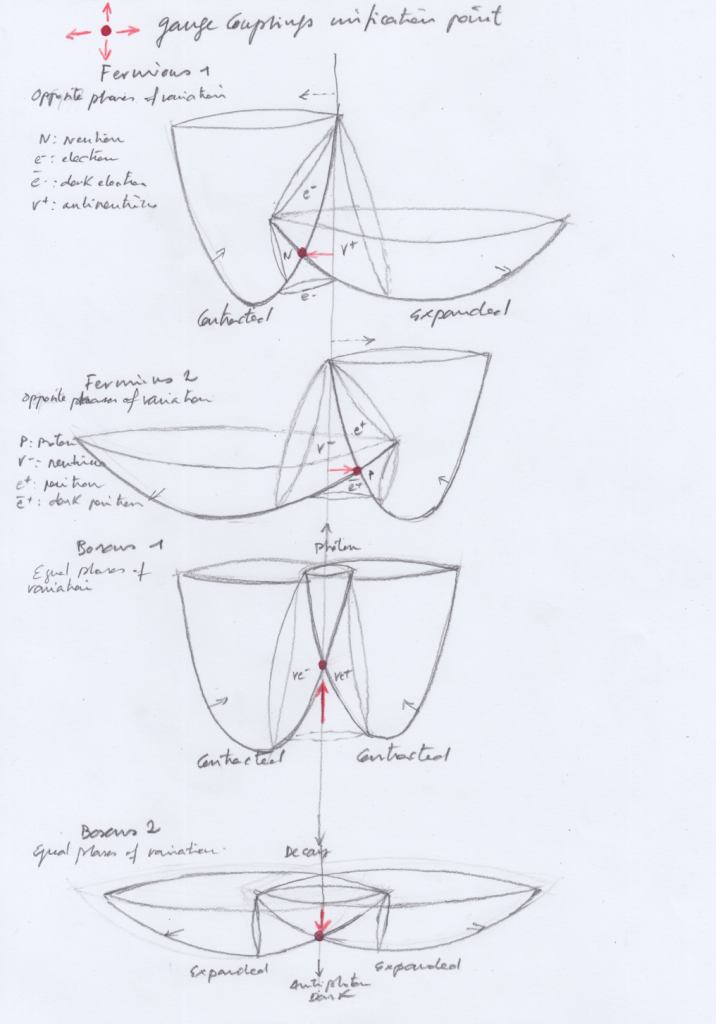
Let’s consider a diagram where two intersecting longitudinal waves form in their intersection a shared nucleus of transversal and orthogonal subwaves distributed by pairs:

The shape, displacements and physical properties of each of these nuclear subwaves will be different depending on the phases of vibration of the intersecting waves. Those phases of vibration could be opposite or equal and, in this system, they will periodically synchronize and desynchronize.
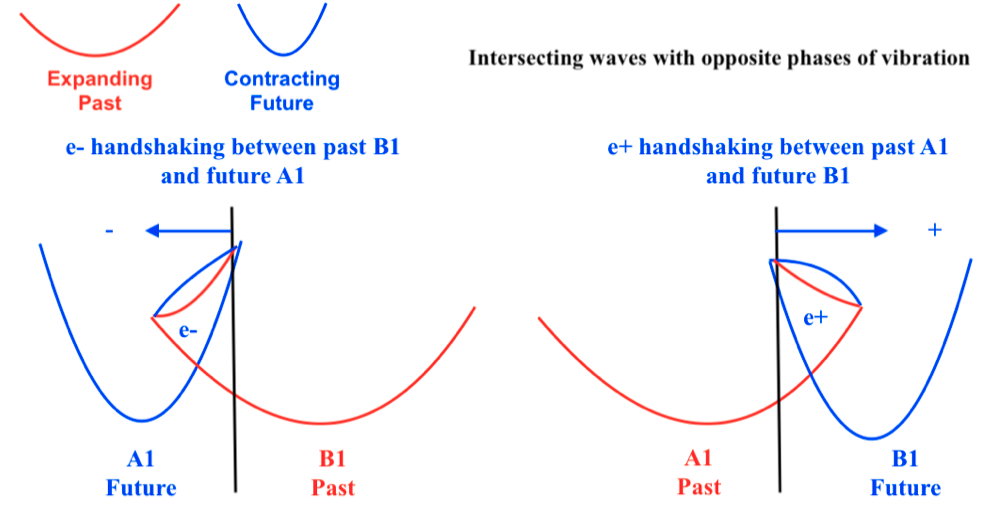
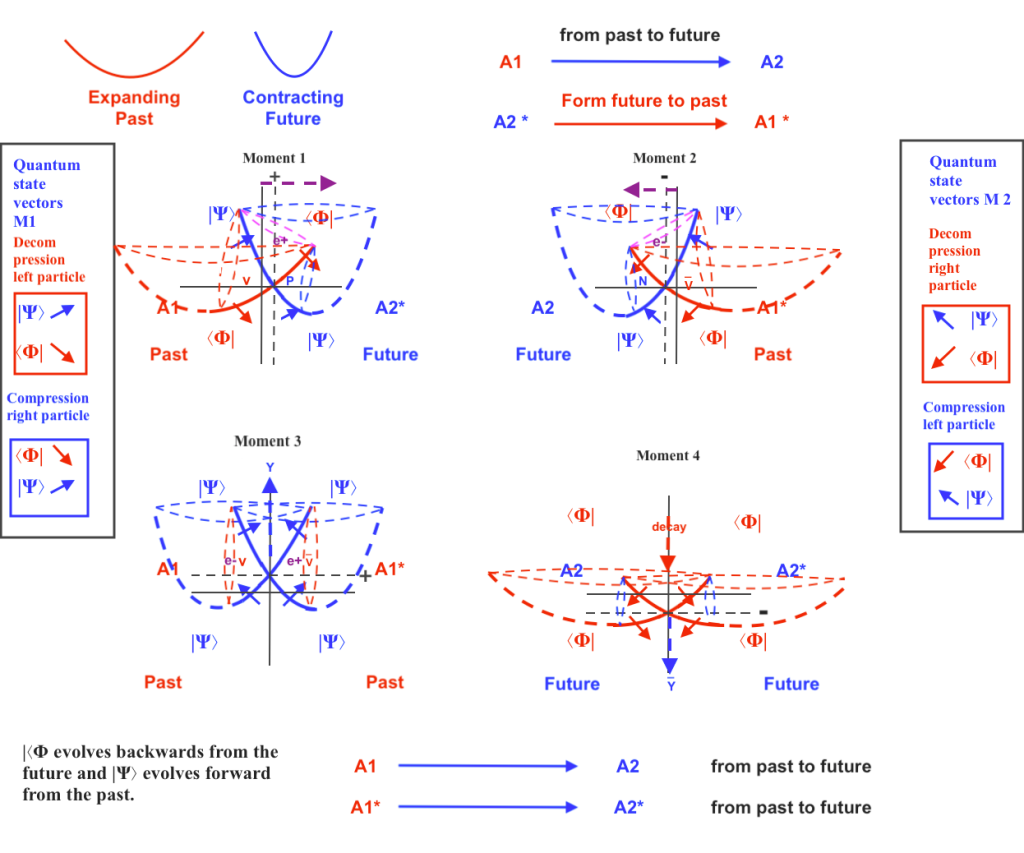
When the phases of vibration of the intersecting waves are opposite, the orthogonal subwave will move towards the side of the intersecting wave that contracts. Moving towards left, the orthogonal subwave will act as an electron; and a moment later, moving towards right, it will act as a positron.
Electron and positron will be then Majorana antiparticles because they will be their own antimatter moving in a pendular way.
Ernst Stueckelberg, and later Richard Feynman, proposed an interpretation of the positron as an electron moving backward in time, reinterpreting the negative-energy solutions of the Dirac equation. Electrons moving backward in time would have a positive electric charge. Wheeler invoked this concept to explain the identical properties shared by all electrons, suggesting that «they are all the same electron» with a complex, self-intersecting world line. (3)
Next will see the figure 4 showing the electron/positron subwave moving from right to left at a moment 1, and later at a moment 2 moving from left to right:
There are several ways of expressing the pendular displacement of the electron/positron subwave and how it’s partially formed by a wave that contracts and a wave that expands.
When at a moment 1 the orthogonal subwave exists as an electron in the left-handed side of the system being formed by the future quantum state of the contracting A1 wave and the past quantum state of the expanding B1 wave, we could think that a transference of energy and material mass has taken place from the right-handed side of the dual system towards its left handed-side.
At a later moment 2, the orthogonal subwave will exist as a positron in the right-handed side of the system which will have taken the energy and mass that will have been lost by the left-handed side of the system. A new transactional exchange will have been completed.
The transactional exchanges will gradually occur while the intersecting waves expand or contract.
The TIQM tells us that the handshaking exchange happens between the retarded past wave and its complex conjugate future advanced mirror symmetric counterpart.

So, it could be said that when the orthogonal subwave exists as an electron at the left side, the next interchange that will create a positron will occur between the advanced contracting A1 wave that will evolve backward to its past expanding state, and the retarded expanding B1 that will evolve forward towards its future contracting state.
On the other hand, to keep the mathematical consistency, it can be state that when the electron/positron subwave moves towards left becoming an actual electron at the left-handed side, at the right-handed side a mirror symmetric positron will exist as a «virtual» particle. It’s virtual because at that specific moment it will not actually exist at the right-handed side of the system, but it has the potential to become actually existing there when just a moment later the left intersecting wave expands and the right-handed one contracts.
The electron/positron subwave is not attracted nor rejected to or from the left or right sides, its displacement is the material effect caused by the curvature’s variation of the intersecting waves that form it. In this sense electronegativity or electro positivity will not be intrinsic properties that matter has per se, they are the geometric consequence of varying spaces that interact between them.
As the electron and it mirror symmetric positron cannot exist at the same moment at the left and right sides of the system, their quantum states are mutually exclusive. In that sense it can be said that electron and positron are ruled by the Pauli Exclusion Principle (PEP), and so they are fermions that will follow the Dirac Fermi statistics.
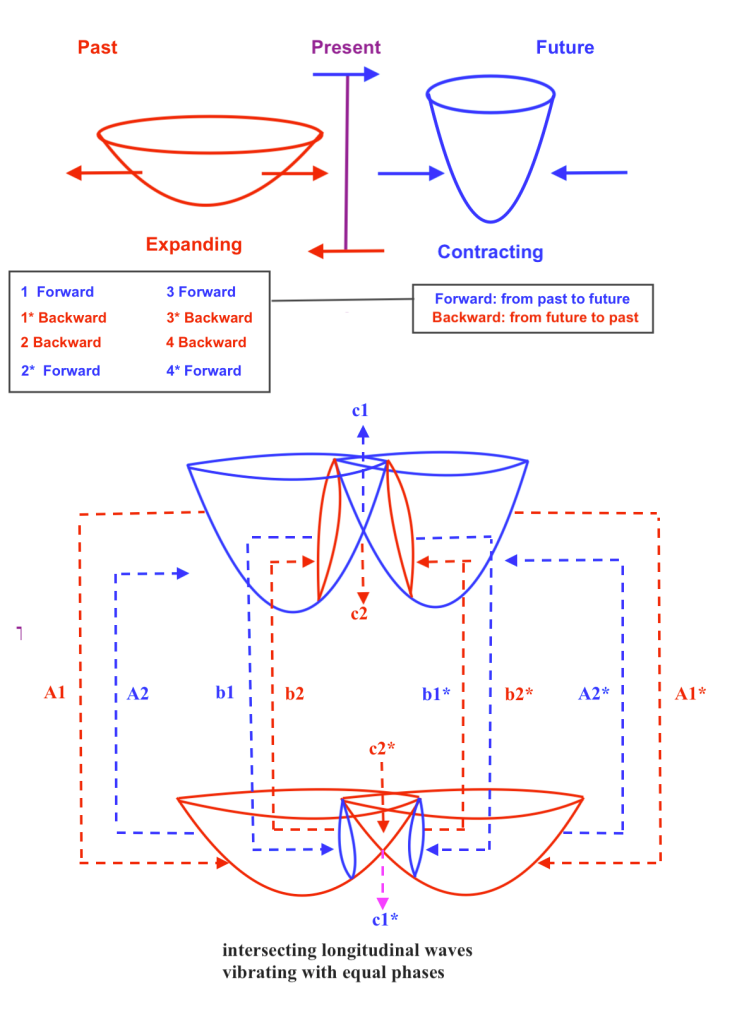
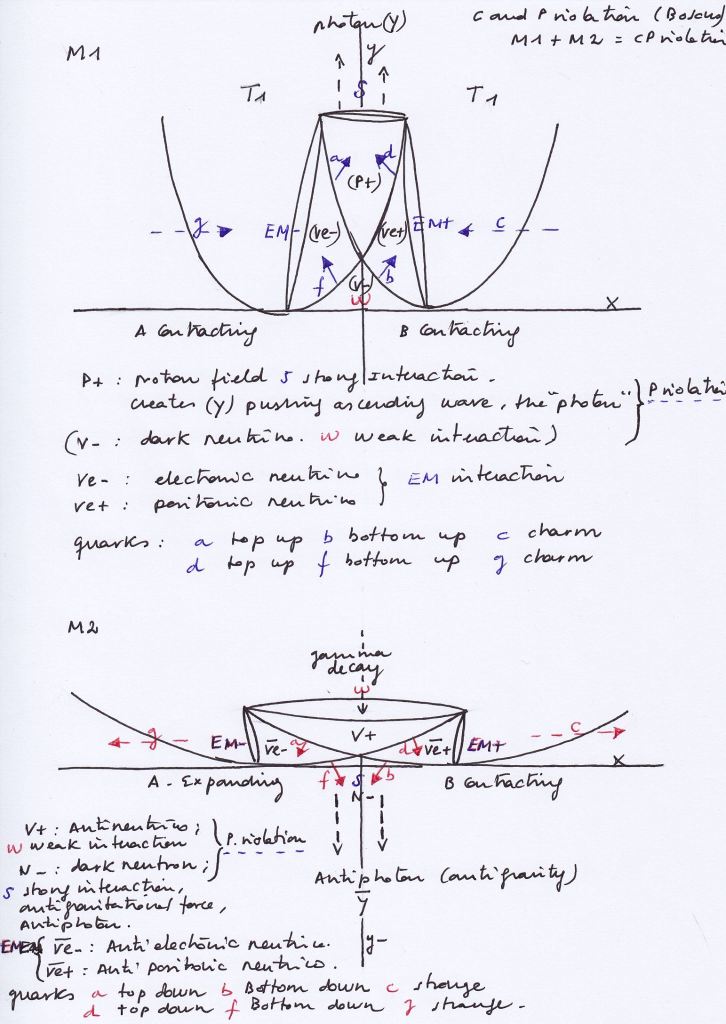
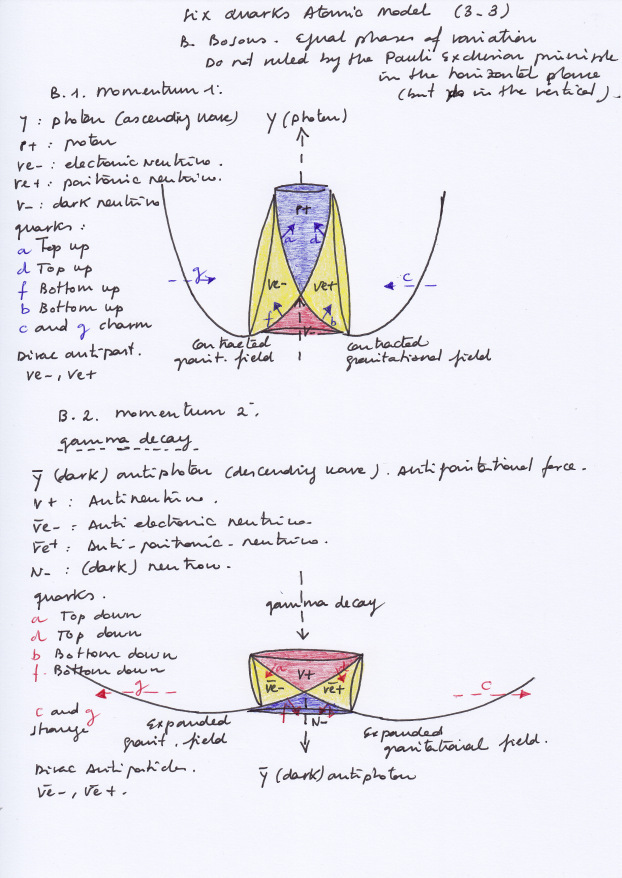
If the phases of vibration of the intersecting waves synchronize becoming equal, the properties and displacements of the orthogonal subwave will change, ceasing to be an electron or a positron. It will experience different forces of pressure or decompression, and it will periodically move in a different way.
So, when both left and right intersecting waves contract the orthogonal subwave will also contract experiencing a double force of pressure and an upward displacement, creating an ascending pushing force that will form a photon.
A moment later, when both intersecting waves expand at the same moment, the orthogonal subwave will experience a double decompression while moving downward, expanding and losing its inner kinetic orbital energy. The previous ascending pushing force will be also lost in what can be considered a decay.
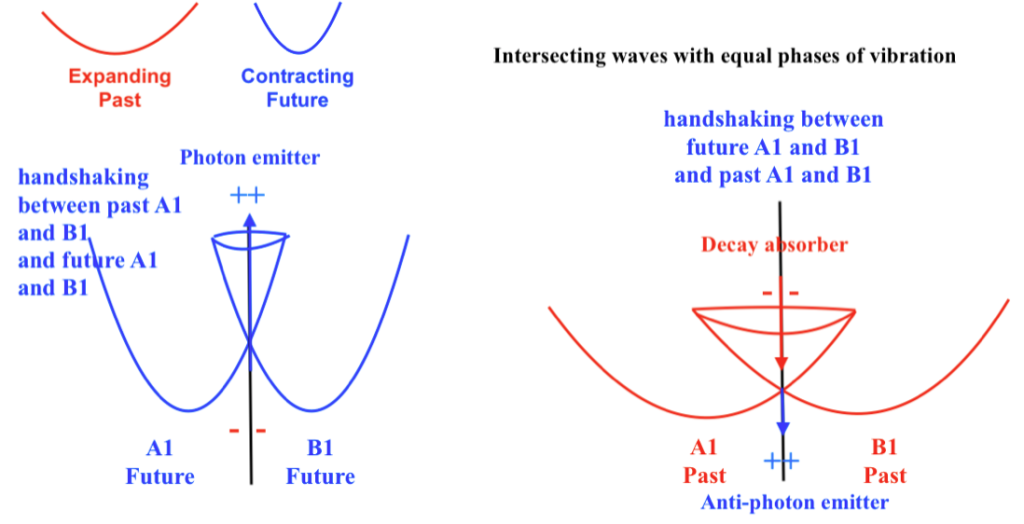
The upward subwave that at moment 1 emits a photon when A1 and B1 have advanced contracting states, should transfer its energy to a retarded mirror conjugate subwave at moment 2, when both intersecting waves A1 and B1 expand.
At moment 2, then, we see that the orthogonal subwave has an expanding state having already lost its kinetic energy and its previous ascending pushing force. Where are then the transferred elements? The transferred energy and force of pressure will be located now at the convex side of the system, creating an antiphoton that will be emitted to an inverted direction. For an observer placed at the concave side of the system the antiphoton will be directly undetectable and will be considered as «dark».
The photon and its decay, or the photon and the antiphoton, cannot occur at the same time. The photon will be a fermion ruled by the PEP.
Photon and dark antiphoton, being different subspaces, would be Dirac antimatters having mirror symmetry at different successive times.
I think this view about the evolution of electron and positron and photon and anti-photon would be aligned with Yoichiro Nambu ideas when, speaking about the production and annihilation of all particles and antiparticles pairs, stated that
«The eventual creation and annihilation of pairs that may occur now and then is no creation or annihilation, but only a change of direction of moving particles, from past to future, or from future to past.» (3)
Let’s analyse now the transactional behaviour of the transversal subwaves when the phases of vibration of the intersecting waves are opposite or equal:
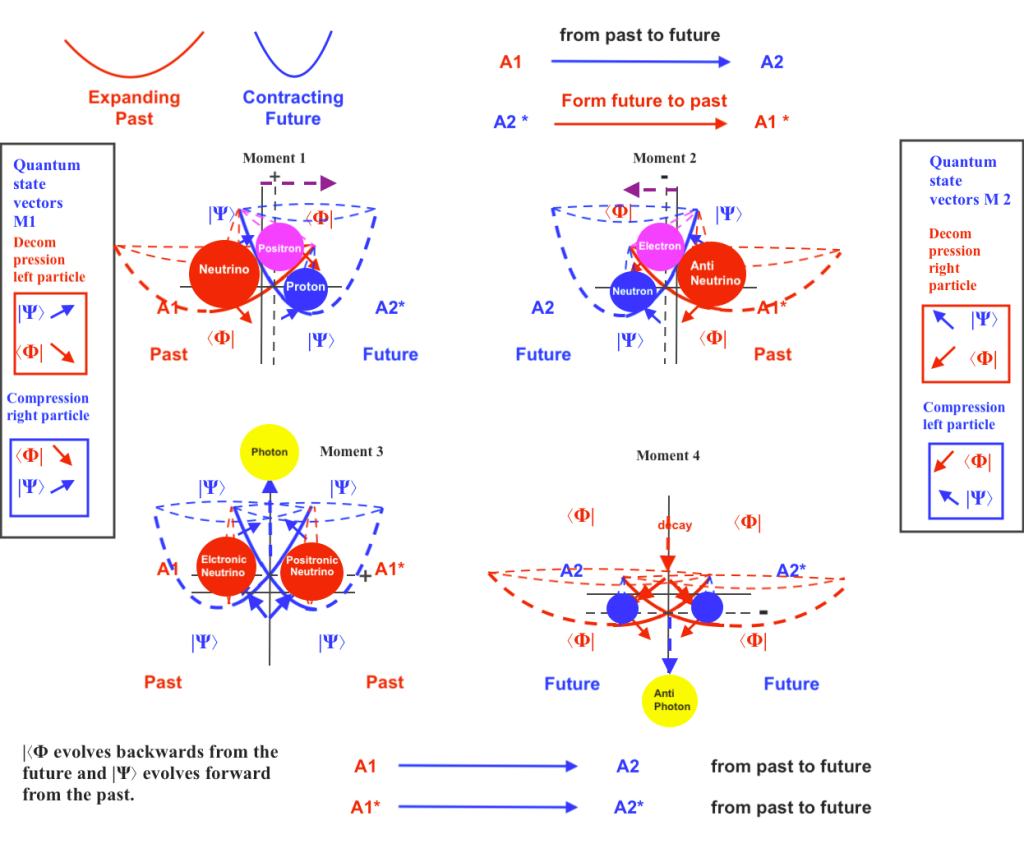
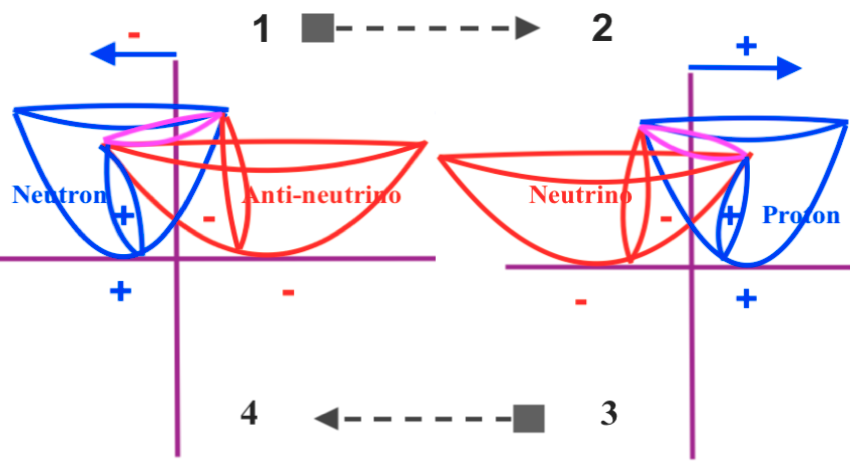
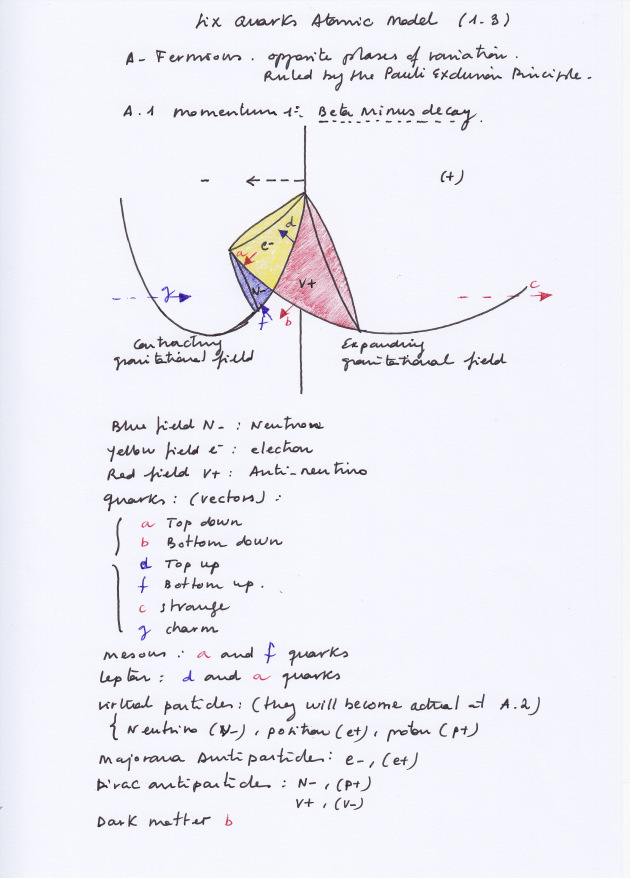
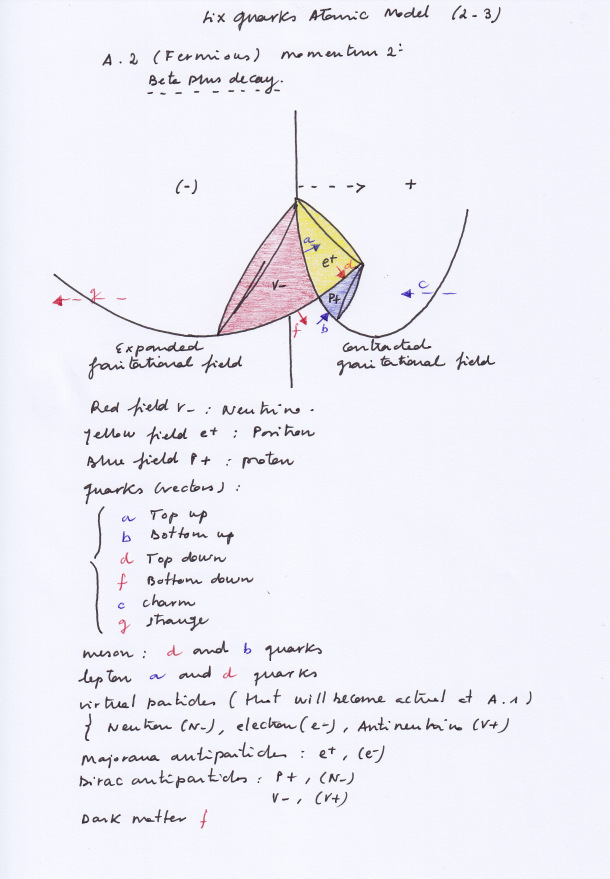
When the phases of vibration of the intersecting waves are opposite, if the left intersecting wave contracts and the right one expands, the left contracting transversal subwave will act as a neutron while at the right-handed side of the system the expanding transversal subwave will act as an antineutrino. A moment later, when the left intersecting wave expands and the right one contracts, the contracting neutron subwave will evolve becoming an expanding neutrino and the expanding antineutrino will evolve becoming a contracting proton.
Neutron and proton, being different subwaves will have mirror symmetry at different successive moments, being Dirac antimatters at different times. The same can be said with respect to neutrino and antineutrino.
Let’s see the whole picture, including the intersecting waves and the formed subwaves-particles:
Maybe it could be easily to visualize the nuclear subwaves showing them as particles
Heisenberg already suggested that neutron and proton would be antimatters, but it’s considered demonstrated as accurately measured that neutron and proton have slightly different masses. However, the proton decay, predicted by mainstream models, has not been observed, remaining a yet unresolved issue.
From the transactional point of view, it could be said that the density, pushing forces and inner kinetic energy that are lost by the left advanced contracting neutron when becoming a left retarded expanding neutrino are obtained by the right expanding retarded anti-neutrino when becoming a right contracting advanced proton.
Thinking that the transactional handshake occurs between mirror symmetric waves, between a wave and its complex conjugate, we could say in this context that the retarded expanding A1 subwave at moment 1 handshakes with the retarded expanding mirror symmetric subwave at moment 2.
When the left subwave is expanding at moment 1 and the right subwave is contracting at the same moment 1, the energy and mass of the system will be located at the right-handed side of the system. But a moment later the system is going to evolve towards a transfer of energy and mass from the right side towards the left, when the left previously expanding subwave contracts while the right previously contracting subwave expands.
We can also think that the transfer of mass and energy occurs though time between the different quantum states of each transversal wave. So, the loss of energy and mass that experiences the left expanding subwave will be recovered by itself a moment later when it will be contracting.
In the same way, a moment later, there will be a handshaking transaction between the contracting proton when becoming an expanding anti-neutrino and the expanding neutrino when becoming a contracting neutron.
In this context, it could be said that a future advanced neutron will act as emitter when handshaking with a retarded past antineutrino; or we could also say that a future neutron will act as the advanced emitter handshaking a transactional exchange with itself in a future time when it will have evolved to an absorber neutrino.
These are terminological disquisitions to be refined, although I think that it would be more accurately to say that when the phases of vibration of the intersecting waves are opposite, the actual transactional exchange is happening between the subwaves that are mirror symmetric at different successive moments, between a subwave and its complex conjugate at different moment: so, an existing neutron will transfer its material properties to a future proton when the past neutron evolves trough the spatial time variation becoming a neutrino at the left side, and a past antineutrino evolves at the right side becoming a proton.
I think this is the way that the waves combine their past and future quantum states to cause a present transactional effect.
When the phases of vibration of the intersecting waves are equal, the quantum states of the left and right transversal subwaves will have mirror symmetry at the same moment.
Here the interchange will take place between the left and right transversal subwaves at a past moment 1 and the left and right transversal subwaves at a future moment 2.
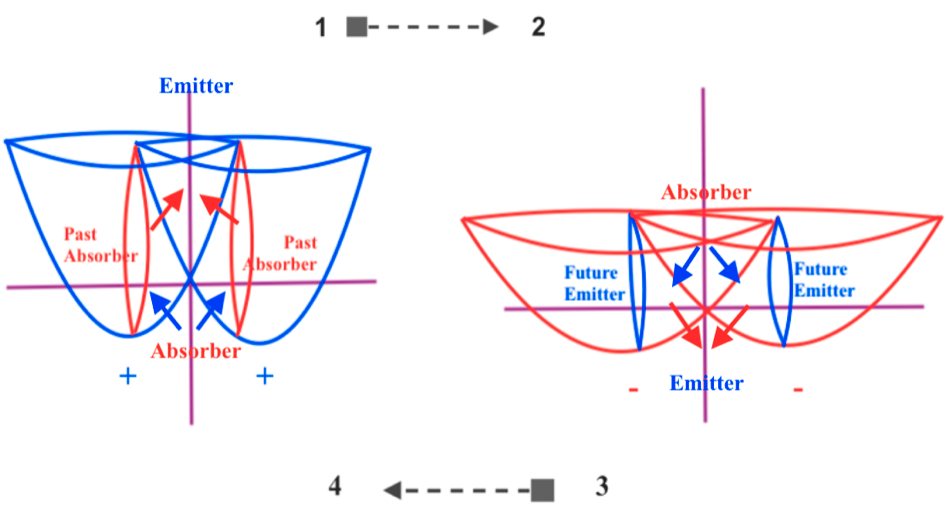
Having mirror symmetry at the same time, the left and right transversal subwaves will have the same quantum state of being expanding or contracting at the same moment, so they won’t be ruled by the PEP and then we can deduce they are bosons that follow the Bose Einstein statistics.
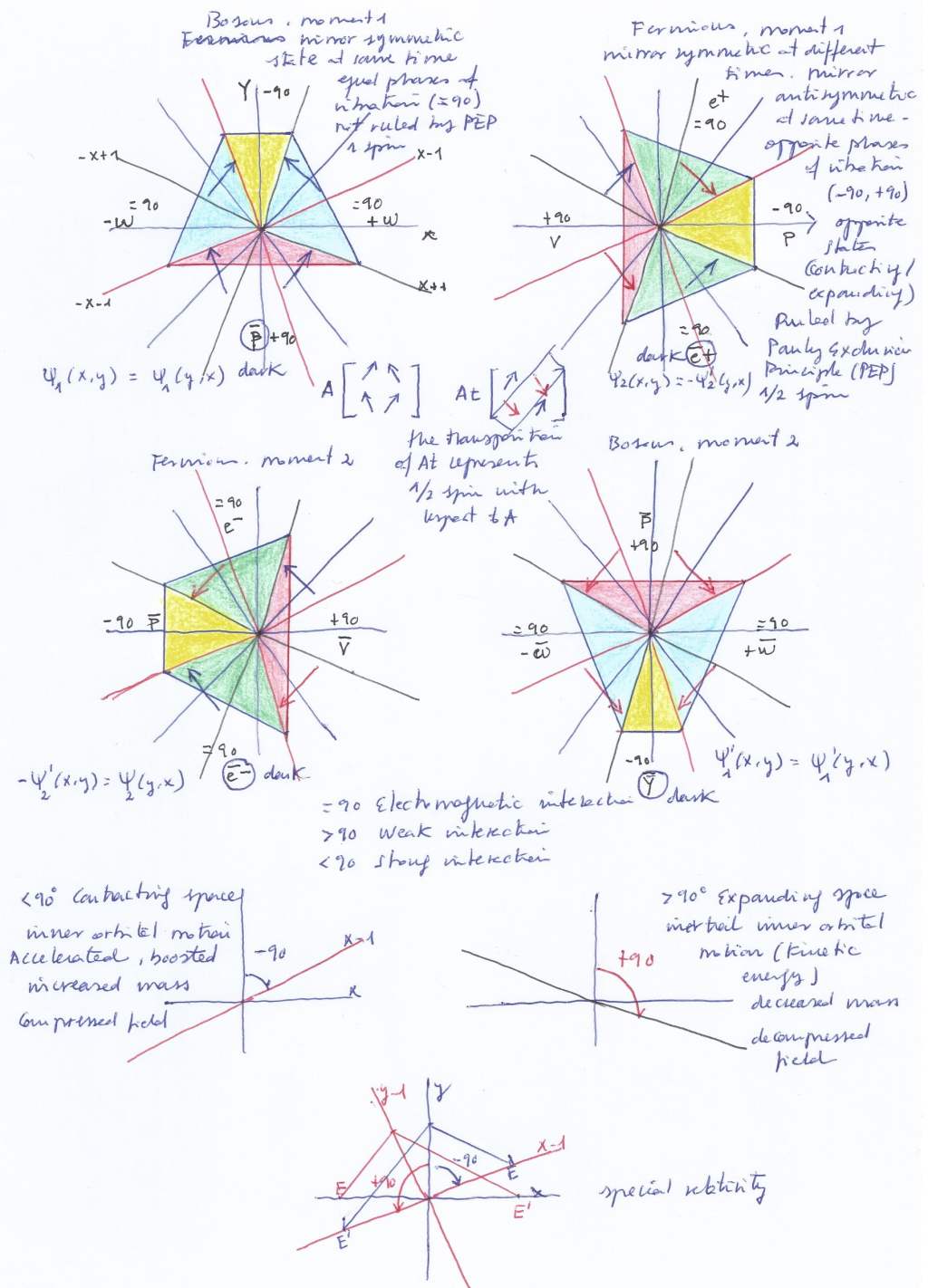
I think the Pauli Exclusion Principle must be considered in terms of mirror symmetry in the context of a composite system. Does the mirror symmetry between the quantum state (of being contracting or expanding) of a subwave and the quantum state of its complex conjugate occur at the same or a different moment? If they occur at a different moment, their mirror symmetric quantum states will be mutually exclusive and the subwaves will be fermions ruled by the PEP; when the mirror symmetry between them occur at the same moment, the mirror symmetric quantum states won’t be mutually exclusive and they will be bosons not ruled by the PEP.
In this kind of composite system, mirror symmetry at the same moment only can occur between quantum states when the phases of vibration of the intersecting waves are equal.
The periodical synchronization and desynchronization of the phases of vibration of the intersecting waves makes the system a topological structure that remains invariant through time. The symmetry between fermions and bosons, being the same subspaces acting in different ways and having different physical properties, is preserved through time because the different forces of pressure they receive and determine their nature while the intersecting waves contract or expand permutate periodically.
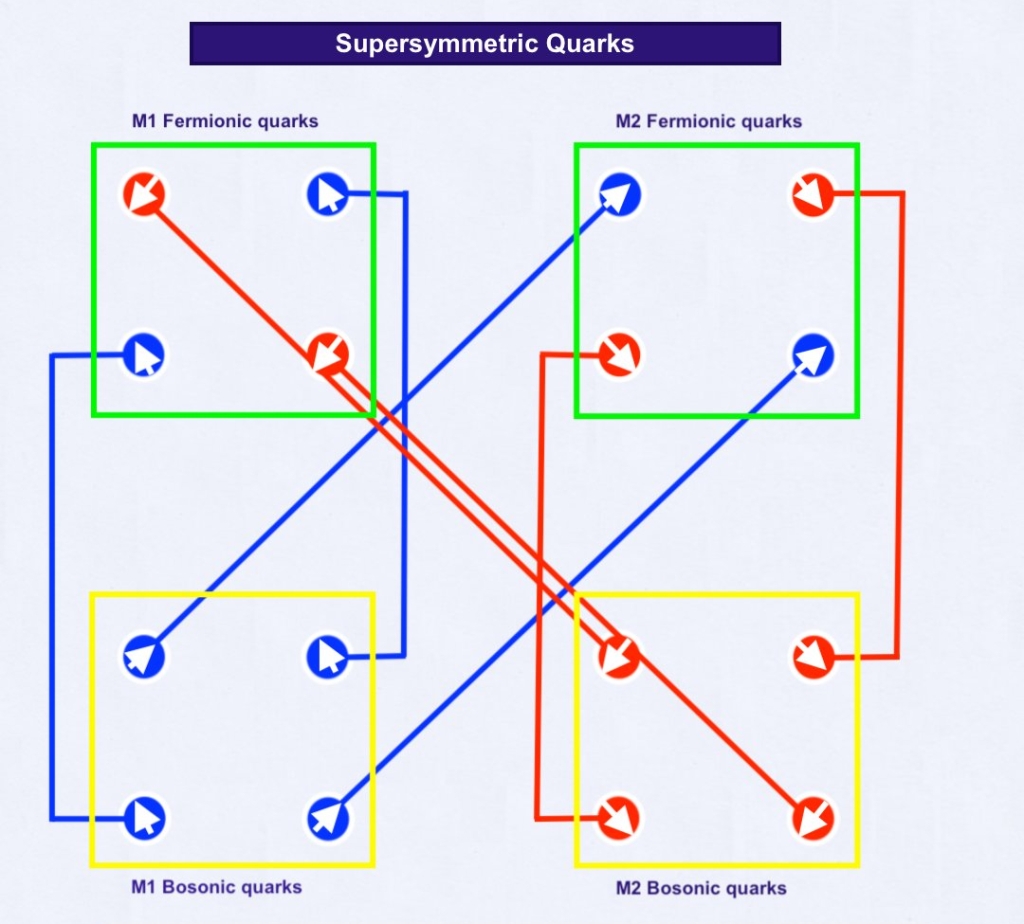
The supersymmetric forces of pressure that are caused by the displacement of the two intersecting waves when contracting and expanding can be represented as vectors of force. Being the force carriers that determine the mass and properties of the subwaves I think they could be considered, using the QCD terminology, as supersymmetric «quarks».
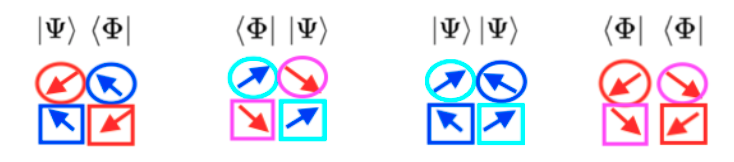
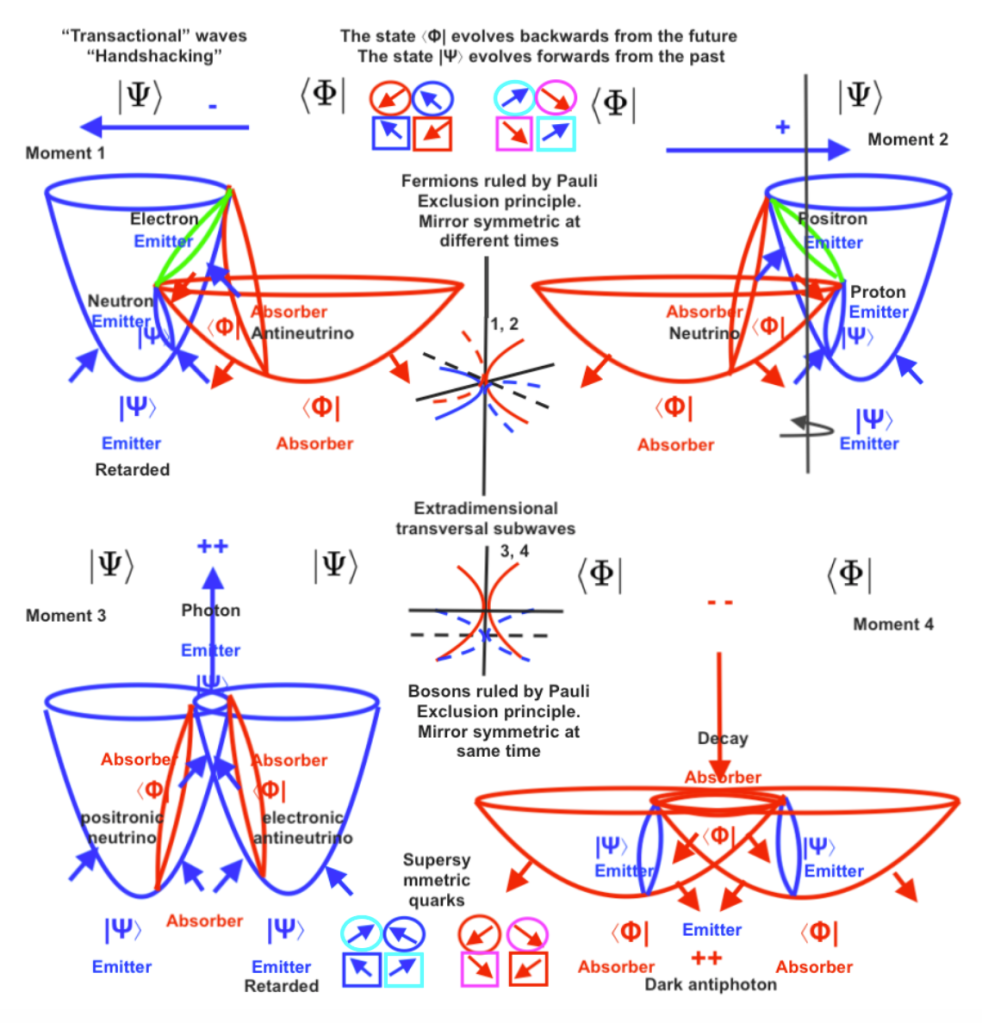
A top-down and a bottom-up quarks, for example, will create a double force of compression that will determine a contracting compressed subwave. Quarks arranged by pairs are the «quantum vector» state of their related subwave.
The supersymmetry of the quarks or pushing force vectors of the system lets explain how the charge and parity symmetries (the CP symmetry, that is currently considered violated) is respected during the whole evolution of the system.
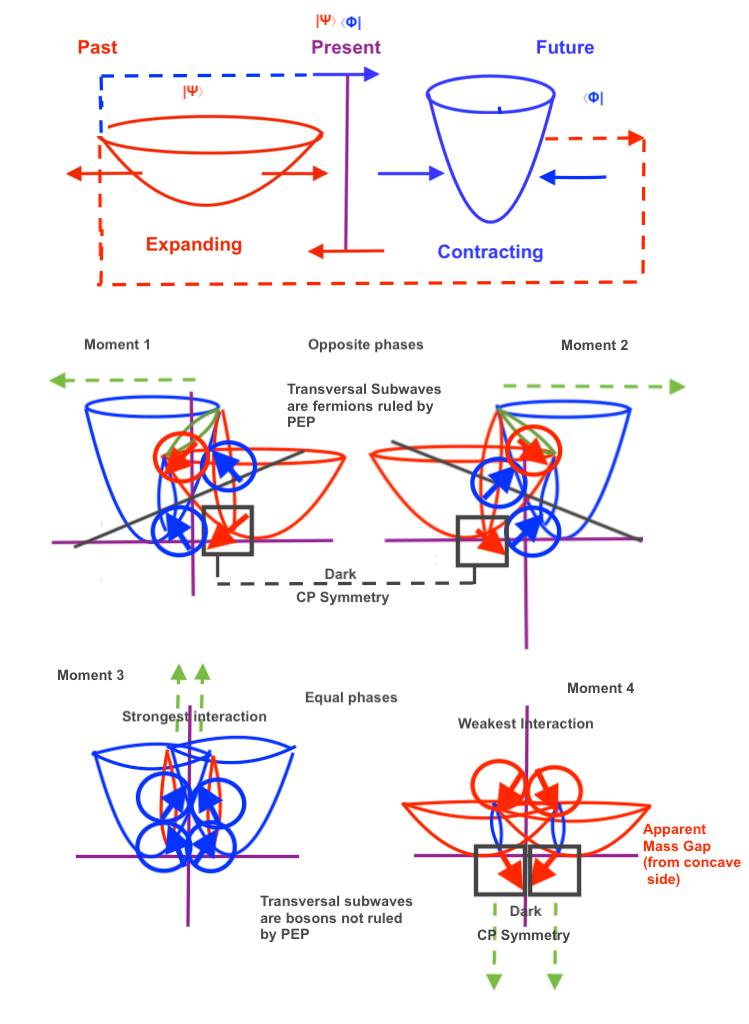
On the above diagrams we see that with opposite phases the blue – vectors of moment 1 have as counterpart the two + blue vectors of moment 2; one of the – red vector of moment 1 has as its counterpart one of the + red vector of moment 2.
Furthermore, there’s a – red vector that works in the convex side of the system at moment 1, that will have as counterpart the + red vector that also works in the convex side of the system at moment 2. These two vectors will be undetectable if the system is being measured only from its concave side. Here we can think that the charge and parity symmetries are preserved through time even without considering the dark red vectors of the convex side, because the two + – blue vectors have two – + counterparts and the – red vector has a + counterpart.
But when the phases of the intersecting waves are opposite, a breaking of symmetry appears from the convex side of the system, because at moment 1 we have four mirror symmetric vectors, but at moment two we only have in the concave side of the system 2 red vectors. So, when the two intersecting waves expand at moment 2, (when the weakest interaction occurs), apparently two red vectors are missing. There are two blue vectors at moment 1 that won’t have a mirror symmetric counterpart at moment 2.
But the CP symmetry gests restored if we look for missing vectors at the convex side of the system. There, two hidden vectors (hidden from the concave side) will represent a double pushing force equivalent to the ascending pushing force that has been lost at the concave side when the decay occurs, creating a dark antiphoton.
Notice that the expanding and contracting intersecting waves cause their pushing forces in a different way. When the wave is expanding, the inward pushing forced will be caused by the inner or concave side of the wave, and when the wave is expanding the outward pushing force caused by its variation will be produced by its outer convex side.
I think this apparent CP violation would be related with the so called «Mass gap» problem.
«State vectors», «Schrödinger equation», etc, are part of the mathematical formalism used by physicists when developing their atomic model. But they are not purely abstract mathematical tools, they refer to the physical topological structures they are trying to describe, even without knowing its geometry, in a mere statistical way.
On the other hand, if we consider the quantum state of being contracting as the quality of being alive and the quantum state of being expanding as the quality of being dead, using the Schrodinger’s cat terminology we could say that when the phases of vibration of the intersecting waves are opposite the left fermionic cat will be alive and, at the same moment, the right fermionic cat will be dead.
Left and right cats are not the same cat, but we can consider them as mirror reflections. If the left alive cat looks at the mirror located at the right-handed side and instead of seeing its own alive reflection it sees its own reflection dead, which normally would seem pretty weird, we will now it’s a fermionic cat, and so what the mirror is reflecting is the quantum state that the left cat will have a moment later. Looking at this oracular mirror that certainly anticipates the future, the left cat will know that in an immediately upcoming future it will die. But it also will know that a moment later it will resurrect.
If the left cat sees its own alive reflection when looking at the mirror, it will be necessarily a bosonic «entangled» cat. The mirror, in this case is only reflecting the present state.
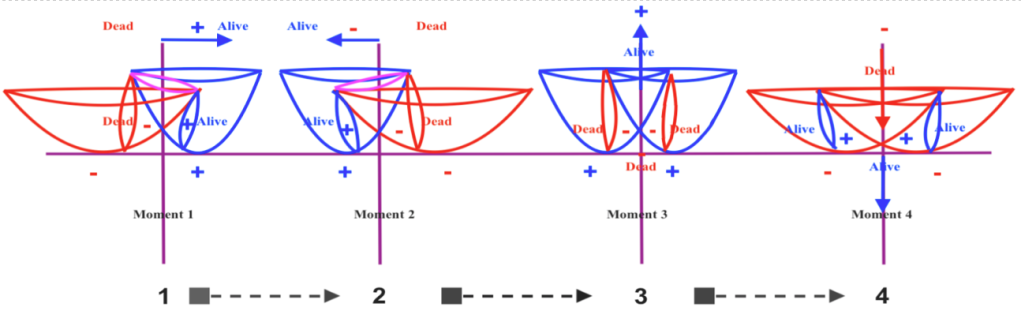
In this sense I think that entanglement and superposition, as it happens with the PEP, must be understood in the context of a composite dual atom in terms of mirror symmetry at same or different times.
A question that remains controversial is what the Schrodinger equation represents, and in the TIQM what its complex conjugate represent.
I think the Schrodinger equation and its complex conjugate represent the variation of the transversal and orthogonal subwaves that are formed by two intersecting waves.
Measuring any part of the intersecting waves will affect the whole shared atomic nucleus.
But being composite by a part of the intersecting waves, the orthogonal transversal can follow the same or an opposite phase of vibration with respect to the intersecting waves.
So, when the phases of vibration of the intersecting waves are opposite, the transversal subwaves will follow the same phase of vibration that the intersecting wave inside of which they are (if the left intersecting wave contracts while the right one expands, the left transversal subwave will contract while the right transversal subwave will expand).
But when the phases of vibration of the intersecting waves are equal, the transversal left and right subwaves will follow an equal phase between them but an opposite phase with respect to the intersecting waves that form them.
Considering then that fermions have opposite phases of vibration between them and bosons have equal phases of vibration between them; considering that fermions follow the same phase of vibration of their closer intersecting wave while bosons follow opposite phases; considering that fermions will evolve into bosons and bosons in to fermions periodically; and considering that the whole composite system will be rotating around its centre, it’s understandable that only a statistical approximation can be obtained with a single Schrodinger wave function.
On the other hand, I think that the Bohm wave pilot interpretation can be easily understood in the context of a composite atom with a share nucleus formed by two intersecting wave pilots. So, for example, the transversal subwave acting as a fermionic electron will be driven towards the left side by the variation of the two wave pilots when the left one contracts and the right one expands.
The Everett’s many worlds interpretation with parallel universes sems to be related with a composite reality. But I think it should be reconsidered thinking in terms of intersecting – instead of parallel – universes, or worlds.
A composite atom would not be probabilistic but a causal and local model.
Chemical bonds would be formed by the inner kinetic orbital motion of the subwaves that would be the subatomic particles. The strong and weak interactions that let the atomic nucleus remain united would be formed by the combination of the symmetric or antisymmetric curvatures of the intersecting waves. So, the weakest interaction – the weakest bond – would occur when both intersecting waves expand at the same moment, while the strongest interaction – the stronger bond – would occur when both intersecting waves contract at the same moment.
It’s thought that the TIQM makes sense of the Born rule that states that the wave function amplitude must be square to get a correct probability when calculating a quantum state. It seems to be a logical consequence of the implication of two mirror symmetric waves instead of a single separate way.
Why do we not guess then that something similar must be happening with the gravitational curvature if distance must be squared to calculate the gravitational force at a macroscopic level?
The heliocentric solar system model, based on a unique field with an invariable curvature, is not able to explain in a mechanic way all the asymmetries that are detected. Being apparently very simple, it’s actually a very complex system where everything seems to have a whimsical position and behaviour: every planet has a different inclination, every orbit has a different eccentricity, every planet orbits at different velocities accelerating and decelerating periodically, and even some planets rotate in an opposite direction.
Copernicus felt compelled to question the old geocentric model because of its unexplained asymmetries. In his own words, the geocentric model seemed to be a monstruous sculpture formed with the different members of very different and unrelated creatures.
Traditionally the quantum world has been considered very bizarre. As a unique orbited space was not a valid geometry to develop the atomic model, the known visual geometric references were forgotten blindly following the abstract algebraic equations and easily accepting the image of the atom as a diffusing cloud where differential equations can be applied. But symmetries and asymmetries were a fundamental clue for finding out antimatter.
Additional figures:

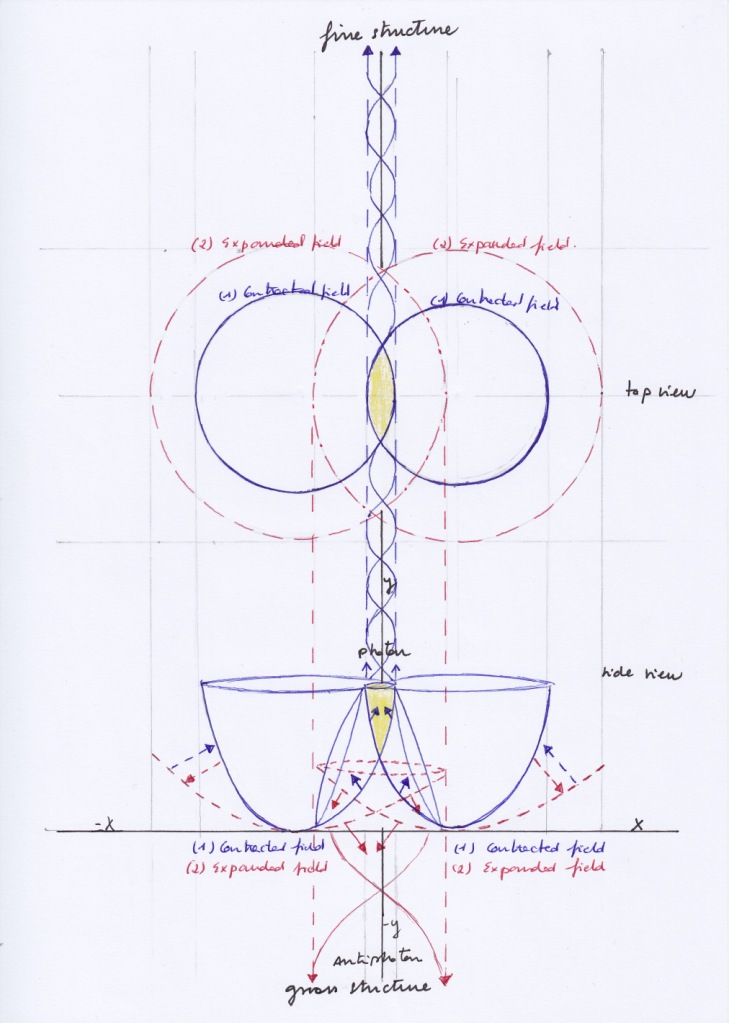

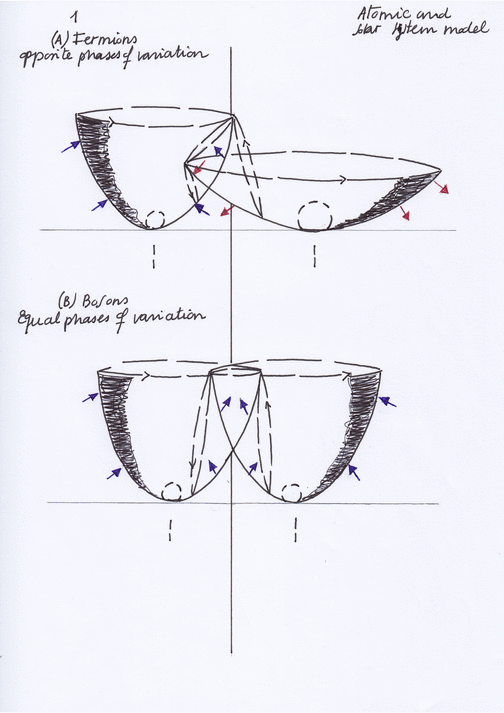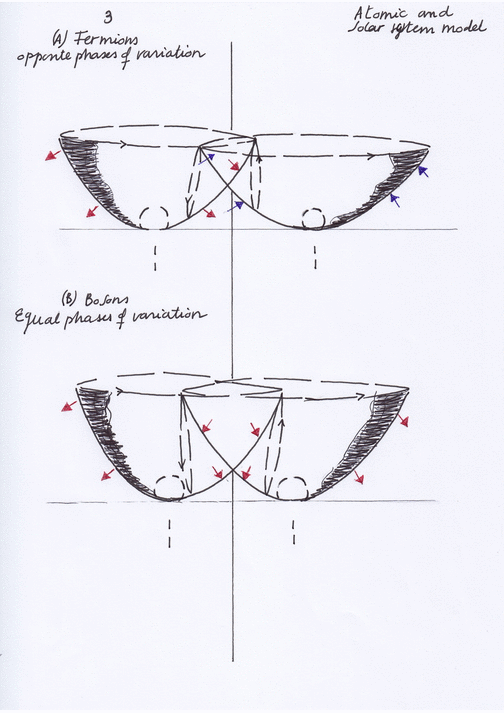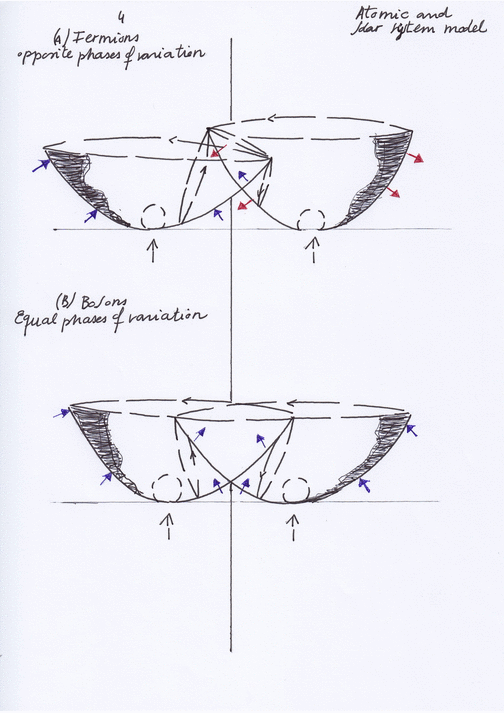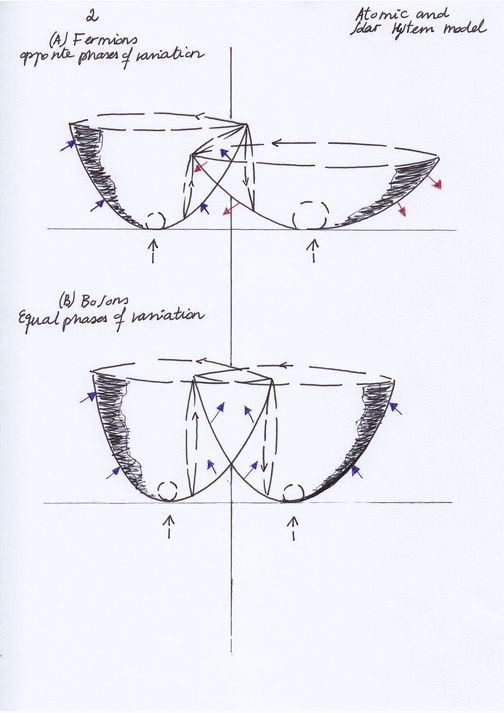
I think these diagrams could be related to the developments known as «Hitching fibration» and to the Higgs mechanism.
For its relation to gravity as a pushing force of pressure see the previous posts on this blog.
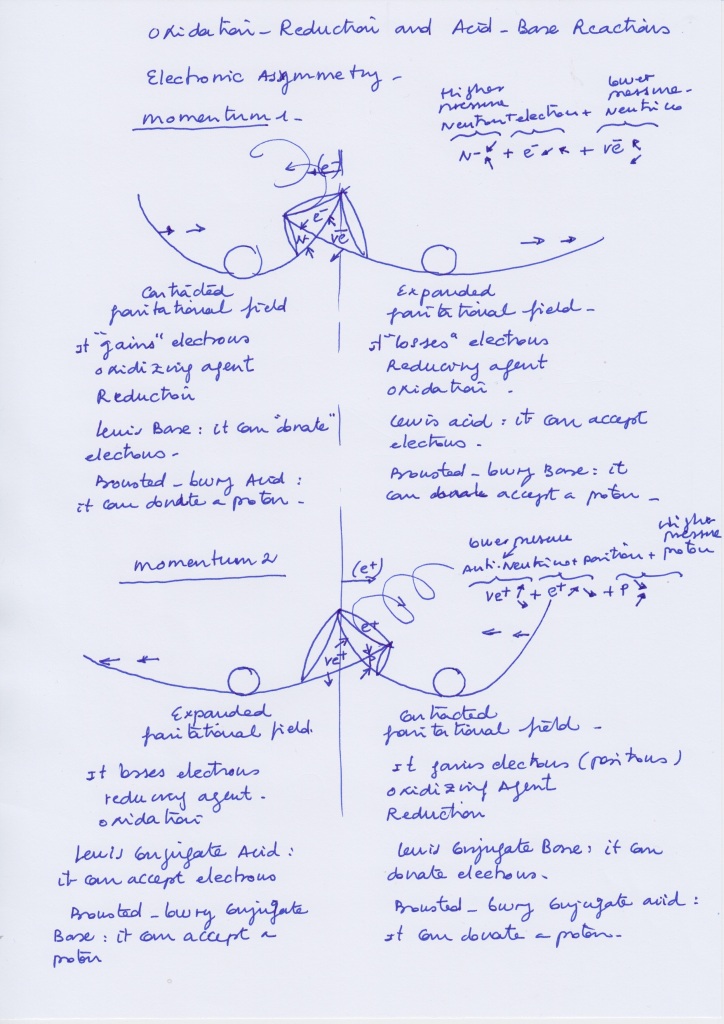
Already in 2014 I wrote a post about Oxidation-reduction and acid-base reactions that I think can be interesting to posted here again.
Electronegativity is considered a measure of the «tendency» of an atom to attract electrons of another atom when forming a chemical bond between them.
Of course, the atom has no «tendencies» nor attractive «abilities». In the view I propose on this blog, electrons are orthogonal subwaves or vibrating subfields moving pendularly left to right while the whole dual atomic system formed by two intersecting waves or vibrating fields rotates around its center.
Redox (reduction–oxidation) is a type of chemical reaction in which the oxidation states of atoms are changed.
- «Oxidation is the loss of electrons or an increase in the oxidation state of an atom, (an ion or of certain atoms in a molecule).«
- «Reduction is the gain of electrons or a decrease in the oxidation state of an atom, an ion, or of certain atoms in a molecule (a reduction in oxidation state).«
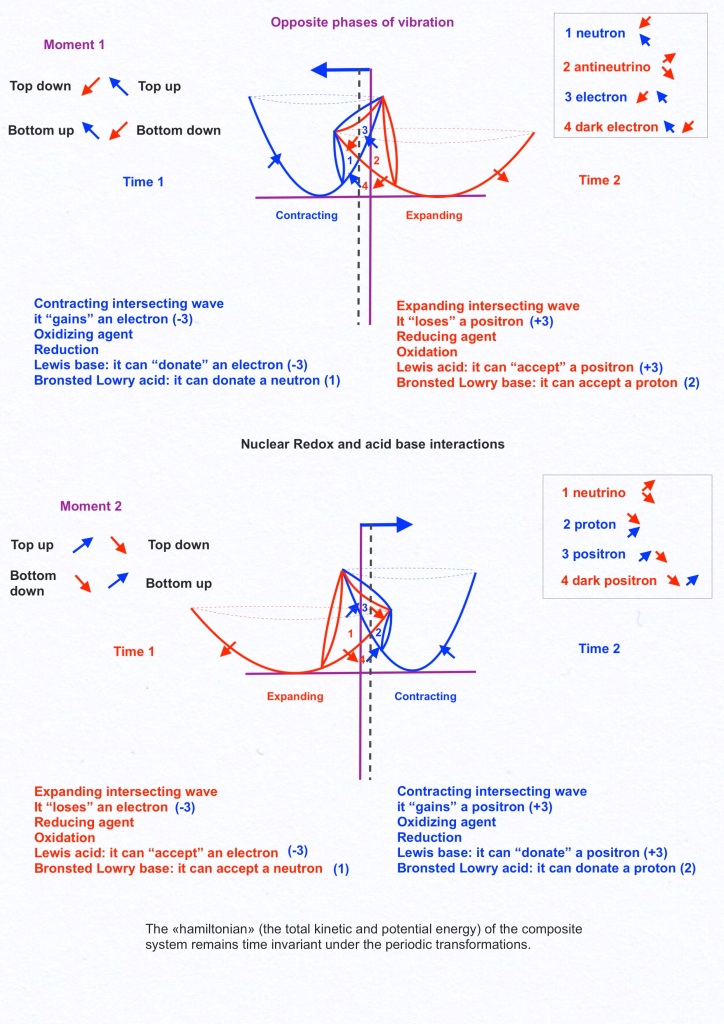
In this sense, considering the composite atomic model of intersecting waves, it’s possible to describe the transactional interchange of energy between the subatomic particles in terms of acid-base or oxidation-reduction events in the context of Feynman-wheeler handshake or the two state vectors type interpretation.
The «hamiltonian» of this time symmetric model (the total kinetic and potential energy of the system) remains invariant under its periodic transformations:
Contracting intersecting wave (with opposite phases):
It “gains” electron (or positron)
Oxidizing agent
Reduction
Lewis base: it can “donate” electron (or positron)
Bronsted Lowry acid: it can donate a proton (or neutron)
Expanding intersecting wave (with opposite phases):
It “loses” positron (or electron)
Reducing agent
Oxidation
Lewis acid: it can “accept” positron (or electron)
Bronsted Lowry base: it can accept a neutron (or proton).
Below I attach the picture I drew seven years ago where I tagged the intersecting waves as gravitational vibrating fields:
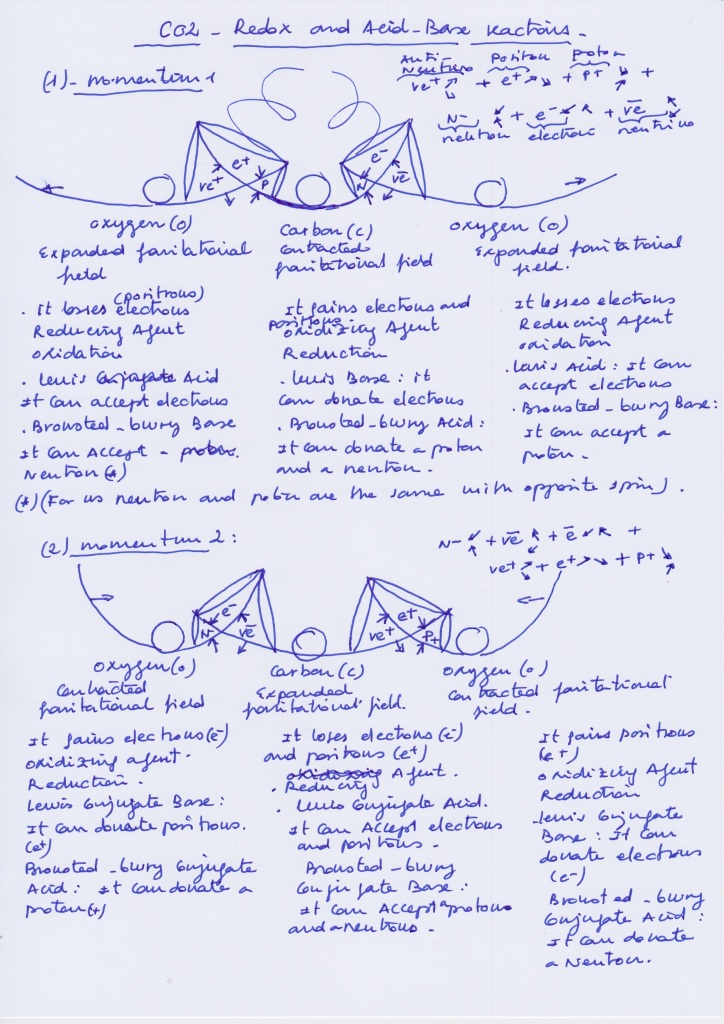
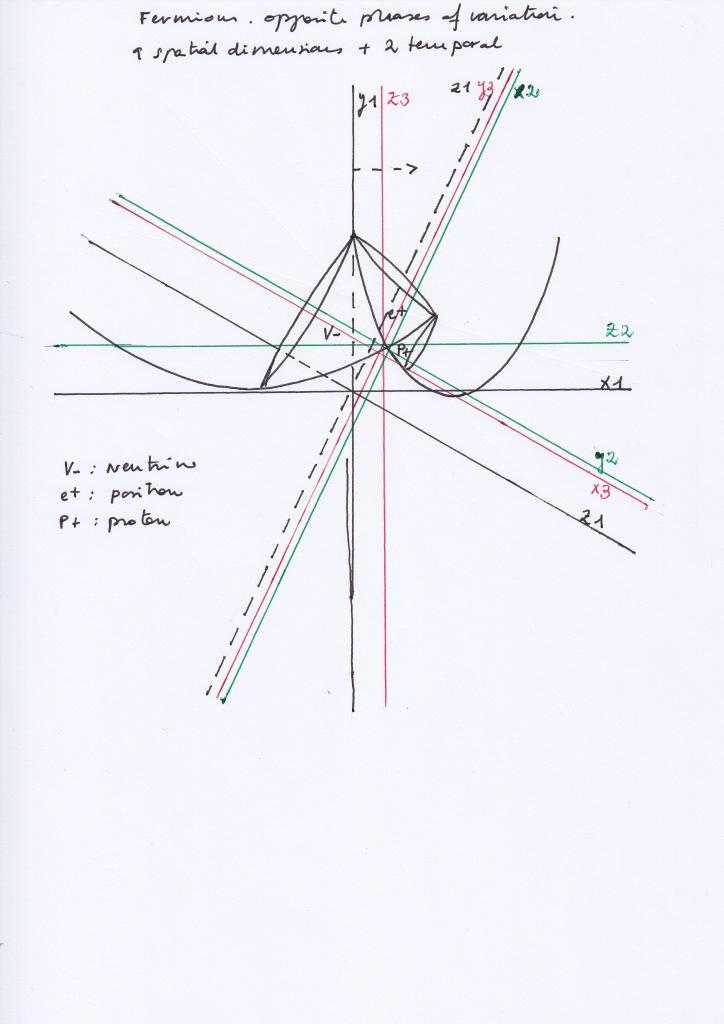
I will also add this old picture I did to show the multidimensionality of the composite model:
and this other kind of diagram with the nuclear interactions when the phases of vibration are oposite, creating the electron/positron subwave, and when the phases of vibration become equal, creating the photon and its decay:

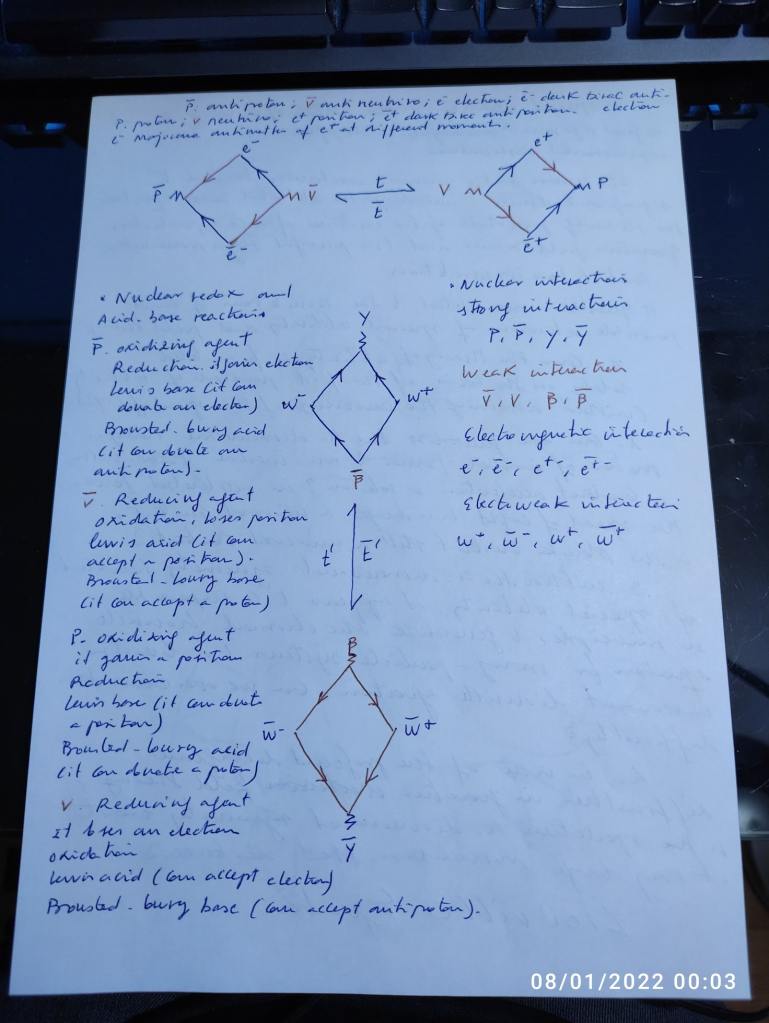
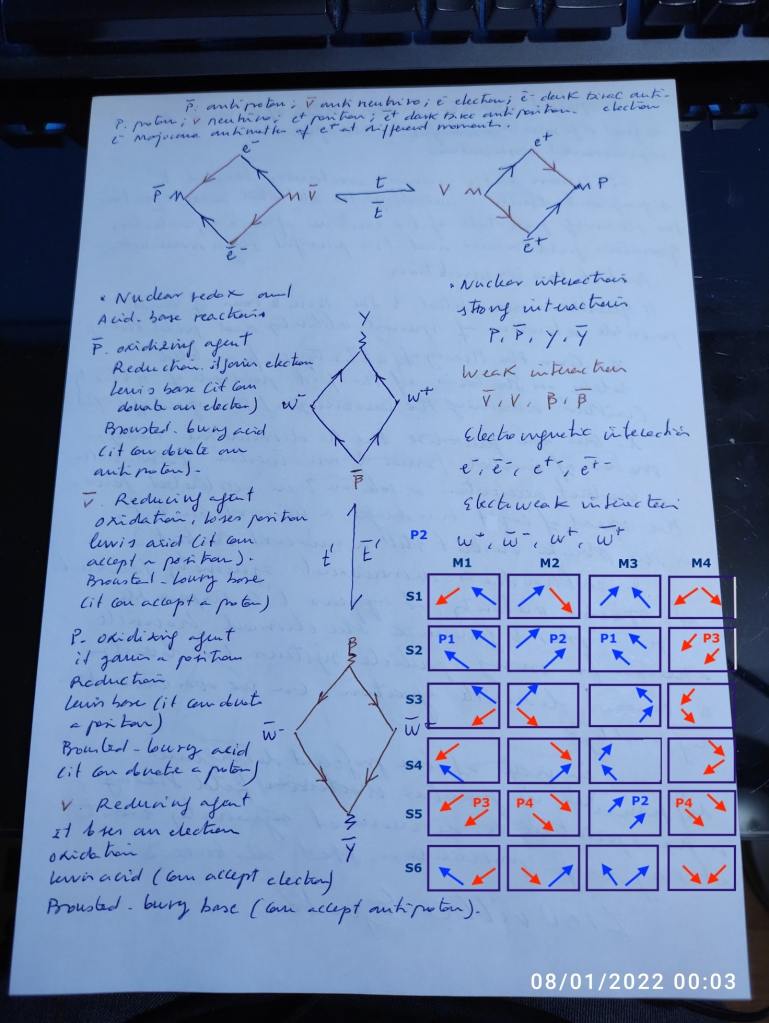
The subatomic vibrating fields or subwaves can also be thought in terms of Klein groups.
The permutations of the force vectors that determine the subspaces’ states of this composite atomic nucleus can also be represented by performing operations of complex conjugation, transposition and inversion on a 2×2 complex matrix. From there, 16 groups of bosonic or fermionic pairs of symmetries, can be formed, corresponding to the evolution of the states of the four (two orthogonal and two transversal) subspaces of the nucleus shared by the dual system.
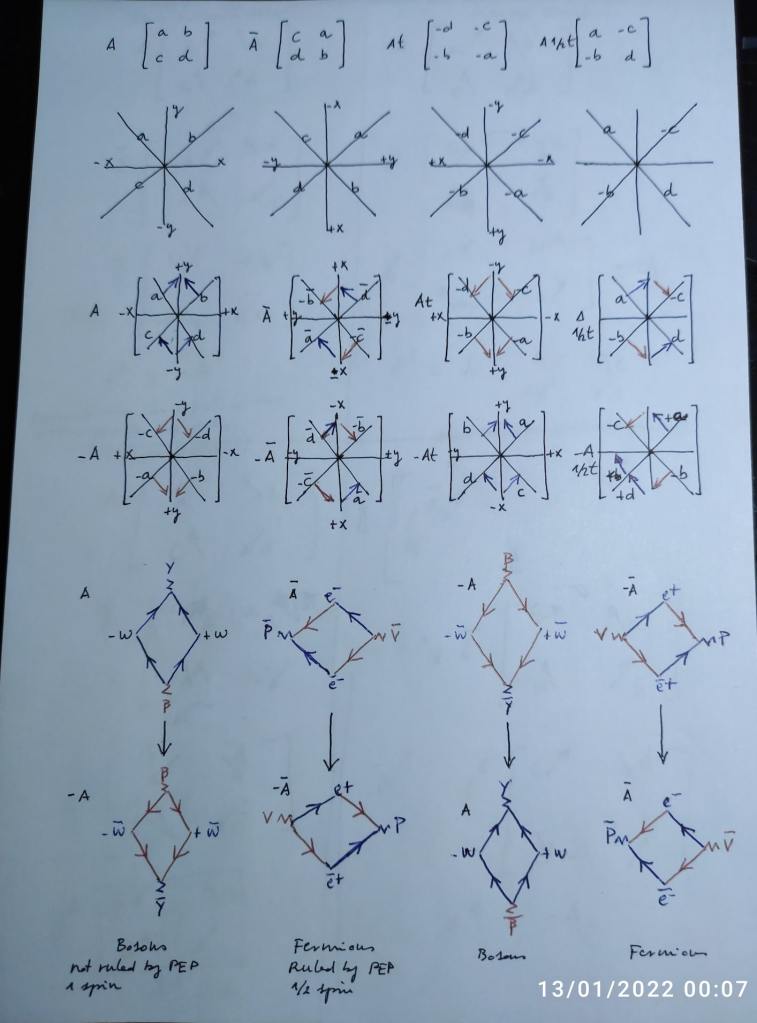
Under this perspective, it’s interesting to see that starting from the initial bosonic matrix A, (that will correspond to the case of both intersecting spaces contracting at the same moment) and, permutating
Under this perspective, it’s interesting to see that starting from the initial bosonic matrix A, (that will correspond to the case of both intersecting spaces contracting at the same moment) and permutating it 90 degrees to perform its complex conjugate (by means of rotating the coordinates of the plane), we get a fermionic matrix (that will correspond to the case where the phases of vibration of the intersecting spaces desynchronize, and the left one contracts while the right one expands), on a 90 degrees rotated plane.
This complex conjugate matrix is equal to the fermionic +A½t transposition. Which is very interesting, because the fermionic -A½t transposition will be equal to the complex conjugate matrix of –A matrix. The bosonic –A matrix corresponds to the moment when both intersecting spaces expand at the same moment.
Fermionic particles have ½ spin and so they respect the Pauli Exclusion Principle. In this sense, the expose diagrammatic waves model is consistent with this matrix model.
The system then would imply an initial set of four complex numbers permuted three times, so a total of four groups of four complex numbers that grouped by determine the initial (past or retarded) and final (future, advanced) states of energy of the atomic subspaces. (Their highest or lowest expansion or contraction).
On the other hand, I think a composite atomic model would let a rational approach to the already abandoned theory of the Dirac’s sea (4).
«The Dirac equation is an extension of the Schrodinger equation consistent with special relativity. Describing successfully electron dynamics, it possesses a rather peculiar feature: for each quantum state possessing a positive energy E, there is a corresponding state with energy –E.
Dirac hypothesized that what we think of as the «vacuum» is actually the state in which all the negative-energy states are filled, and none of the positive-energy states. Therefore, if we want to introduce a single electron, we would have to put it in a positive-energy state, as all the negative-energy states are occupied.
Dirac further pointed out that a situation might exist in which all the negative-energy states are occupied except one. This «hole» in the sea of negative-energy electrons would respond to electric fields as though it were a positively charged particle. Initially, Dirac identified this hole as a proton. However, Oppenheimer pointed out that an electron and its hole would be able to annihilate each other, releasing energy on the order of the electron’s rest energy in the form of energetic photons; if holes were protons, stable atoms would not exist.
The issue was finally resolved in 1932, when the positron was discovered by Carl Anderson, with all the physical properties predicted for the Dirac hole.»
From the perspective of the model here proposed, the Dirac thought behind the apparently absurd ideas of a sea and hole can be logically understood and related to the ideas of transactional energies mentioned before.
If there’s a positive energy at the left side of the system because the orthogonal subspace moves as an electron towards left (when the left intersecting space contracts and the right-handed one expands) and the left transversal subspace contracts as an antiproton with its inner kinetic energy accelerating, at the left side of the system the will be a space of negative energy: a previous contracting right transversal proton with positive energy that will now be transformed into an expanding right transversal antineutrino.
In the same way, when a moment later the right intersecting space contracts and the left-handed one expands, the right negative energy transversal subspace (the past expanding antineutrino) will contract becoming a right positive energy transversal subspace (the actual contracting proton); at the same moment, at the left side of the system, the previous positive energy subspace that was the previous contracting antiproton will decay into a negative energy subspace, the actual expanding neutrino.
The Dirac’s «hole» intuition has meaning when it comes to the scenario of the electron/positron orthogonal subspace moving in a pendular way left to right and right to left. Because when it moves towards left acting as a negative electron, at that moment it will not exist at the right side where it previously existed as a positron. Then, at the right side of the system there will be a negative energy subspace: the antineutrino. The antineutrino occupies at the right side the space left by the positron when moving towards right becoming an electron, and the antineutrino also occupies the space of the previous proton, because it is an evolved or decay state of the proton.
On this perspective it’s very interesting to see how Dirac imagined those see of negative energy fully occupied and how he later allowed an empty hole to be occupied.
Dirac also mentioned two types of electrons, with an up and with a down spin. And in this respect, the electron down spin can be thought as the bottom down vector in the case of opposite phases, that would be dark electron because it will operate at the convex side of the system, on the dark hyperbolic subspace. In this sense it could be possible to think about a Dirac antielectron, that would be the mirror symmetric hyperbolic subspace on the parabolic side the of the system, and a Majorana antielectron (the same electron moving toward right as a positron).
I spoke in this post and the blog in terms of longitudinal and transversal waves instead of intersecting vibrating fields and orthogonal and transversal vibrating subfields to use the ave terminology. I think it could be less confusing for physicists to use the term «vibrating fields» and subfields with varying curvatures. For the relation of the model with gravity I will remit you to previous posts.
I already reached the free limit of 3 Gb given by the free blog platform that runs the blog.
I think this is a beautiful way of finishing the blog with this post, adding some of the first pictures I did at the beginning.
I feel I already developed the model as far as I could, and I’m very happy about it.
I’m convinced that soon or later it will start to be evident the old geocentric model of a single, separate, and static field orbited around its center that still remains implicit in the currently accepted atomic and solar system models is not enough to explain nature, and that a step forward to dynamic and composite atomic and gravitational models is needed.
Maybe, who knows, 2022 will be the year when the laurel will grow green again.
References:
1 . https://en.wikipedia.org/wiki/Two-state_vector_formalism
2 . https://en.wikipedia.org/wiki/Transactional_interpretation
3. https://en.wikipedia.org/wiki/Retrocausality
Bibliography:
Wikipedia: Wheeler–Feynman absorber theory
Wikipedia: Feynman–Stueckelberg interpretation
«By considering the propagation of the negative energy modes of the electron field backward in time, Ernst Stueckelberg reached a pictorial understanding of the fact that the particle and antiparticle have equal mass m and spin J but opposite charges q. This allowed him to rewrite perturbation theory precisely in the form of diagrams. Richard Feynman later gave an independent systematic derivation of these diagrams from a particle formalism, and they are now called Feynman diagrams. Each line of a diagram represents a particle propagating either backward or forward in time. In Feynman diagrams, anti-particles are shown traveling backwards in time. This technique is the most widespread method of computing amplitudes in quantum field theory today.
Since this picture was first developed by Stueckelberg, and acquired its modern form in Feynman’s work, it is called the Feynman–Stueckelberg interpretation of antiparticles to honor both scientists».
Michael Satosi Watanabe: «Symmetry of Physical Laws: Part 3, prediction and Retrodiction«
John Cramer: «The Quantum Handshake: Entanglement, Nonlocality and Transactions«.
Ruth Kastner: «The transactional interpretation and its evolution into the 21st century: an overview»
Copernicus: » De revolutionibus orbium coelestium», preface.
David Griffiths: «Introduction to Elementary Particles» (2nd ed.).
Paul Helpern: «The Quantum Labyrinth: How Richard Feynman and John Wheeler Revolutionized Time and Reality».
Aditional links:
Forbes, Nov 17, 2017: «Richard Feynman And John Wheeler Revolutionized Time, Reality, And Our Quantum Universe»
PDF version at Academia.edu
———————————
Additional bibliography:
«Time in Quantum Mechanics», vol 1. Gonzalo Muga, R. Sala Mayato, I. Egusquiza Editors, Chapter 13: «The Two-State Vector Formalism: An Updated Review» by Yakir Aharonov and Lev Vaidman.
Symmetries of N times N non-Hermitian Hamiltonian matrices by A Alaña, S Martínez-Garaot, M A Simón and J G Muga
«Two-time interpretation of quantum mechanics» by Yakir Aharonov and Eyal Y. Gruss
«Quantum Dialogue: The Making of a Revolution» by Mara Beller
«The Problem of Time: Quantum Mechanics Versus General Relativity« by Edward Anderson
———————————
Summarizing email:
I finally will ad the summary I wrote for this post, as I think it’s a bit clearer:
«Two States Vector in a Composite Dual Atomic Model:
I start from considering a longitudinal wave that vibrates as a single quantum system, thinking about its state of being highly expanding as a past quantum state |Ψ⟩ that will evolve forward to the future state of being highly contracting, and its state of being highly contracting as the future quantum state ⟨Φ| that will evolve backward to the past state of being highly expanding.
Past and present are here arbitrary referential values that we assign to the system independently of the measures we can do, to refer the evolution of the system while varying its curvature through time, in a similar way that we attribute a negative sign to a left handed field and a positive sign to a right handed field to reference them in a space.
I think that time is measure that we do about the variation that occurs in a static space or in a varying space, or the measure we do about the variation of the space itself. Here, past and present are arbitrary referential values to indicate that the wave is expanding or contracting. I think it makes sense when instead of a single space we have a composite manifold of intersecting spaces and subspaces that vary with same or opposite phases.
Then, considering a composite model of two intersecting longitudinal waves vibrating with same or opposite phases, there will be two orthogonal subwaves and two transversal subwaves forming a cobordian nucleus shared by the dual system.
A highly expanding transversal subwave |Ψ⟩ that stars to contract will represent a past quantum state whose curvature evolves forward to a future highly contracting state; and a highly contracting transversal subwave ⟨Φ| (being ⟨Φ| the complex conjugate of |Ψ⟩ ) that stars to expand will represent a future quantum state that evolves backward to a past highly expanding state.

When the phases of vibration of the intersecting waves are opposite, a handshaking transaction will take place between the left and right transversal subwaves in terms of density, volume, inner kinetic energies, or experienced pushing forces, emitted or absorbed at the same moment. (It also can be considered that the transference happens between the past retarded and future advanced quantum states of a same subwave).

In this sense, considering the composite manifold of as dual composite atom with a shared nucleus, if the left intersecting wave contracts as – ⟨Φ| while the right one expands as +|Ψ⟩, the orthogonal subwave will move towards left acting as an electron; the left transversal subwave will be contracting acting as a – ⟨Φ| anti proton; and the right handed transversal subwave will be expanding acting as a + |Ψ⟩ anti neutrino. When a moment later the left intersecting wave expands acting as – |Ψ⟩ and the right one contracts acting as + ⟨Φ|, the orthogonal subwave will move toward right acting as a + positron; the left – ⟨Φ| contracting transversal subwave will evolve to a – |Ψ⟩ expanding subwave that will be a neutrino; and the right + |Ψ⟩ expanding transversal subwave will evolve to a + ⟨Φ| contracting subwave that will be a proton.

It was already suggested by Heisenberg that the proton would be the antimatter of the neutron, but i think they will be mirror symmetric antiparticles at different successive moments. (I know currently is considered experimentally very well probed that proton and neutron have different masses, but one of the problems that remain unexplained by the Standard model is the proton’s decay). Neutrino and antineutrino would also be Dirac antimatters at different moments.
In this context, the quantum states of being contracting (or expanding) of neutron and proton subwaves cannot occur at the same moment. If the left transversal subwave has a contracting quantum state acting as neutron, at the right side of the system the transversal subwave will be expanding acting as an antineutrino. In the same way, when the left transversal subwave acts as an expanding neutrino, the right transversal subwave will act as a contracting proton.
In a similar way, when the electron/positron orthogonal subwave moves towards left acting as an electron, it cannot simultaneously exist at the right handed side acting as a positron. That orthogonal subwave moving pendularly left to right would be a Majorana antiparticle, because it’s the same subwave acting as electron or positron at different moments . When it acts as an electron moving towards left, the mathematical formalism can be saved by saying that at the right side there will be a «virtual» positive positron, it will be actually inexistent then but it has the potential of being actually existing there a moment later. (The electron is not attracted to left nor rejected from right, its displacement is a consequence of the variation of the curvatures of the intersecting waves that pilote or drive it towards the side of the intersecting wave that contracts).
I think that is in terms of mirror symmetry how the Pauly Exclusion Principle should be interpreted in a composite model. In this sense, neutron and proton, neutrino and antineutrino, electron and positron will be «ruled» by the PEP, and so they must be fermions following the Dirac fermi statistics if this were a probabilistic model.
Also, considering both the Schrodinger wave function and its complex conjugate, I think that superposed quantum states should be interpreted in terms of subwaves that are mirror symmetric at same or different times.
In that sense the Schrodinger cat will not be a single cat with two simultaneously opposite quantum states (of being alive and dead) but two distinguishable cats, each one being the mirror reflection of the other at a same or at a different moments.
If the expanding quantum dead cat appears as a contracting alive cat at its mirror reflection, it will imply that the left and right transversal cats are fermionic cats ruled by the PEP and that the mirror reflects a retarded or advanced quantum state of the other cat.
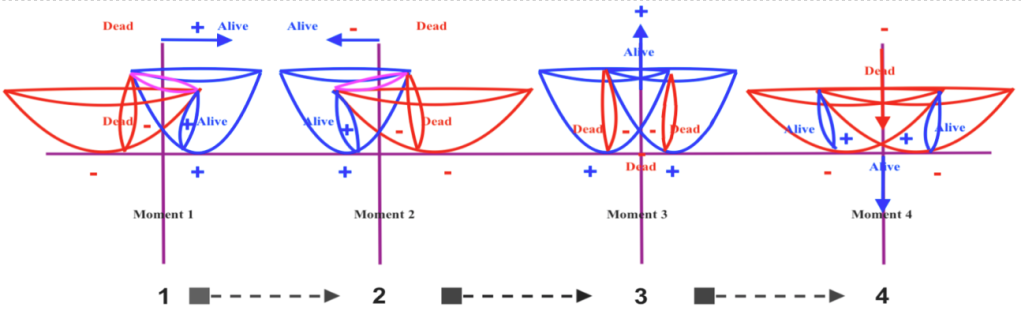
When the quantum states of both left and right transversal cats are the same, being simultaneously alive (or dead), they will be bosonic cats not ruled by the Pauly Exclusion principle.
When the phases of vibration of the intersecting waves are equal and both waves contract, the orthogonal subwave will contract while moving upward, causing a pushing force that will create a photon. When a moment later both intersecting waves expand, the orthogonal subwave will expand experiencing a decay of energy and a loss of its previous pushing force.
When the decay occurs, taking place the weakest interaction of the system, the lost pushing force and inner orbital kinetic energy will be transferred to the mirror symmetric counterpart orthogonal subwave formed at the convex side of the system, creating a dark antiphoton. It will be dark because for an observer measuring the system from its convex side it will be directly undetectable.
I think that considering that convex side of the composite system, the CP violation will be fixed. Also I think that convex side would be related to the so called «Mas Gap» problem.

Having the intersecting waves equal phases, the transversal subwaves will have the same phase of vibration between them, having mirror symmetry at the same moment, and an opposite phase with respect to the intersecting waves. Notice that when the transversal waves acted as fermions (when the intersecting waves had opposite phases) they followed the same phase than the intersecting wave which its borders each one is located in.
I represented with vectors the pushing forces caused by the outer or inner sides of the intersecting waves while expanding or contracting. I think those vectors of force would represent «quarks» in QCD.
As the intersecting system would synchronise and desynchronise periodically, the periodical permutation of the quark vectors would make the system symmetric through time, so supersymmetric:

On the other hand, the whole system would rotate around its center, so there would be only four rotating subatomic subwaves.
But it’s not clear to me if those kind of transversal subwaves could exist in reality because it seems the inner orbital motions of each intersecting wave would affect to the inner orbital motion of the transversal subwave in whose domain they are located.
Some additional pictures:





Cheers.