This preprint introduces in a visual and conceptual way a model of two intersecting curved fields with a shared nucleus, whose quantized dynamics offer potential cases of the four-variable Jacobian conjecture and a nonlinear Hodge cycle.
The model’s Kummer-type geometry suggests a unified framework where abstract mathematical developments like Tomita-Takesaki, Gorenstein, and Dolbeault theories can be conceptually linked to the Jacobian and Hodge conjectures.
Several mathematical physics topics, like the mass gap problem, releflection positivity, the arise of an imaginary time, t-duality, or the connection between string and field theories are also described within this context.
Finally, the model proposes a novel deterministic quantum atomic system with a dual nucleus structure of matter and mirror antimatter.
Tthe left and right transversal subfields of the dual nucleus of the intersecting fields model can be considered algebraic varieties of projective spaces (the coordinates of the intersecting fields are projected onto the diagonal to constitute the extradimensional coordinates of the transversal subspaces). In the antisymmetric system, there is an algebraic cycle in the cohomological group composed of the algebraic variety of moment 1, and by its inverse variety at moment 2. In the symmetric system, there is another algebraic cycle in its cohomology group that relates its two algebraic varieties. The combination of the algebraic varieties of both groups gives rise to a supergroup whose cycle can be considered a Hodge cycle. The Hodge conjecture proposes that Hodge cycles are linear combinations of algebraic cycles. However, in the intersecting fields model, where the curvatures of space are quantized by means of the rotation of the system, the combinations of those algebraic varieties are nonlinear. This implies that the atomic model with a dual nucleus of matter and antimatter could be described in terms of Hodge cycles, and that the Hodge conjecture is formulated in a limited framework of classical linearity that does not take into account the quantization of curved spaces.
Los campos transversales izquierdo y derecho del modelo atómico de campos intersectados son variedades algebraicas de espacios proyectivos (las cooordenadas de los campos intersectados se proyectan hacia la diagonal para constituir las coordenadas extradimensionales de los subespacios transversales). En el sistema antisimétrico se da un ciclo algebraico en el grupo cohomológico integrado por la variedad algebraica del momento 1, y por su variedad inversa en el momento 2. En el sistema simétrico se da otro ciclo algebraico en su grupo de cohomología que relaciona sus dos variedades algebraicas. La combinación de las variedades algebraicas de ambos grupos da lugar a un super grupo cuyo ciclo se conoce como ciclo de Hodge. La conjectura de Hodge propone que los ciclos de Hodge son combinaciones lineales de ciclos algebraicos. Sin embargo, en el modelo de campos intersectados, donde las curvaturas del espacio están cuantizadas, las combinaciones de las variedades algebraicas son no lineales. Ello implica que el modelo átomico con nucleo dual de materia y antimateria puede describirse en términos de ciclos de Hodge, y que la conjectura de Hodge está formulada en un marco limitado de linearidad clásica que no tiene en cuenta la cuantización de los espacios curvados.
**An updated version, 2024/02/22, can be read/downloaded on the next pdf **
Keywords
Jacobian, Gorenstein, supersymmetry, mirror symmetry, Tomita-Takesaki, modularity, mass gap, reflection positivity, quantum field theory, dual nucleus, antimatter, t-duality, SYZ conjecture, elliptic fibration, Calabi-yau, Higgs field, Hodge cycles, Kummer surfaces, Wirtinger derivatives, Dolbeault cohomology, Riemann Zeta function, visual geometry, complex plane.
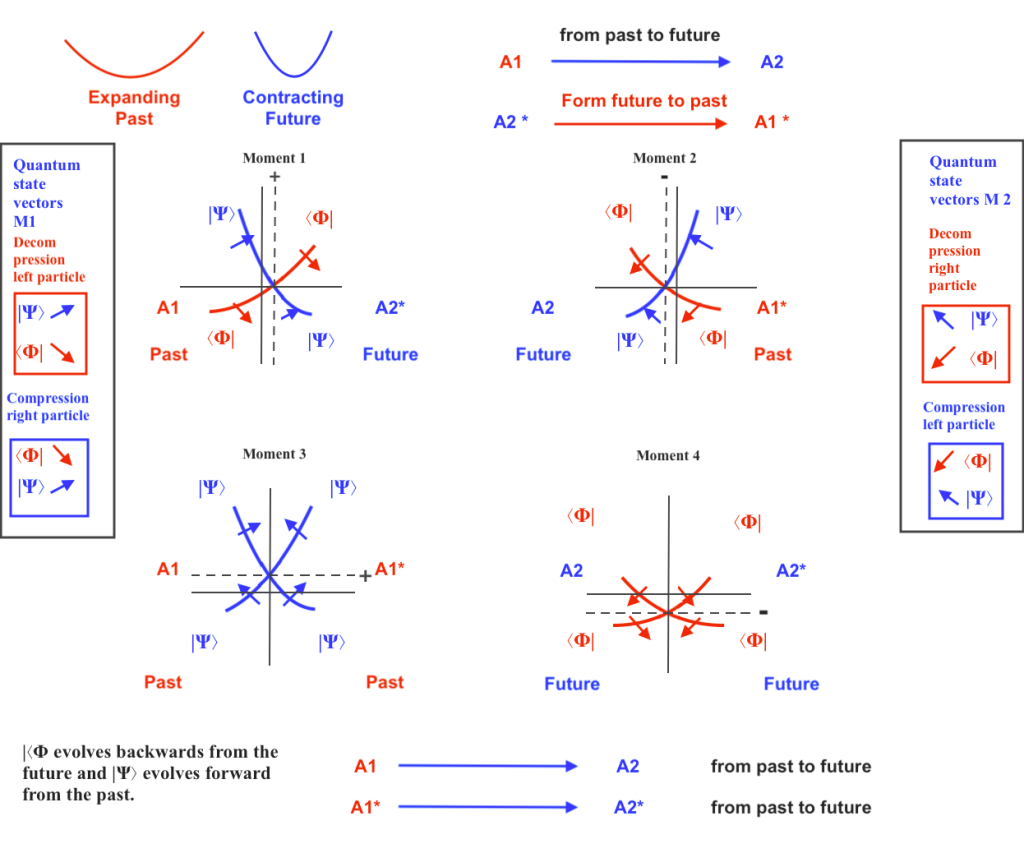
1. Antisymmetric system
We start by considering an antisymmetric system of two intersecting fields that vary with opposite phase, when the right field contracts the left expands and vice versa. In their intersection they form two transverse and two vertical subfields. The transverse subfields are mirror antisymmetric, when the right subfield expands the left contract and vice versa.

Fig 1. Represents the two moments of the antisymmetric system. At moment A2, the right transverse subfield contracts and the left expands. Later, at moment A4, the right transverse subfield expands and the left contracts.
The curvature of the transverse subfields is half positive and half negative, and they are determined by the forces of pressure caused by the inward displacement of the negative curvature of the contracting field determined, and by the outward displacement of the positive curvature of the expanding field.
Those forces of pressure are represented by four eigenvectors with eigenvalue 1 or -1.
An actual inversion equivalent to a 180 degrees rotation is operated when the right-hand contracting field expands and the left expanding field contracts. Then, the right contracting subfield at A2 is mapped to the left contracting subfield at A4, and the left expanding subfield at A2 is mapped to the right expanding subfield of A4.
In that way, the left and right transversal subfields exhibit chiral mirror symmetry at different times. This is because half of the system follows a purely imaginary time dimension, delayed with respect the real time dimension that follows the other half of the system.
However, both left and right transverse subfields are described by the same spatial dimensions. Those dimensions cannot be the same that are used to describe the intersecting fields, because the Y coordinate one of the transversal subfields will be considered a diagonal axis from the point of view of the coordinates system of the intersecting fields. Misleading the coordinates would introduce a relativistic space-time elongated metric.
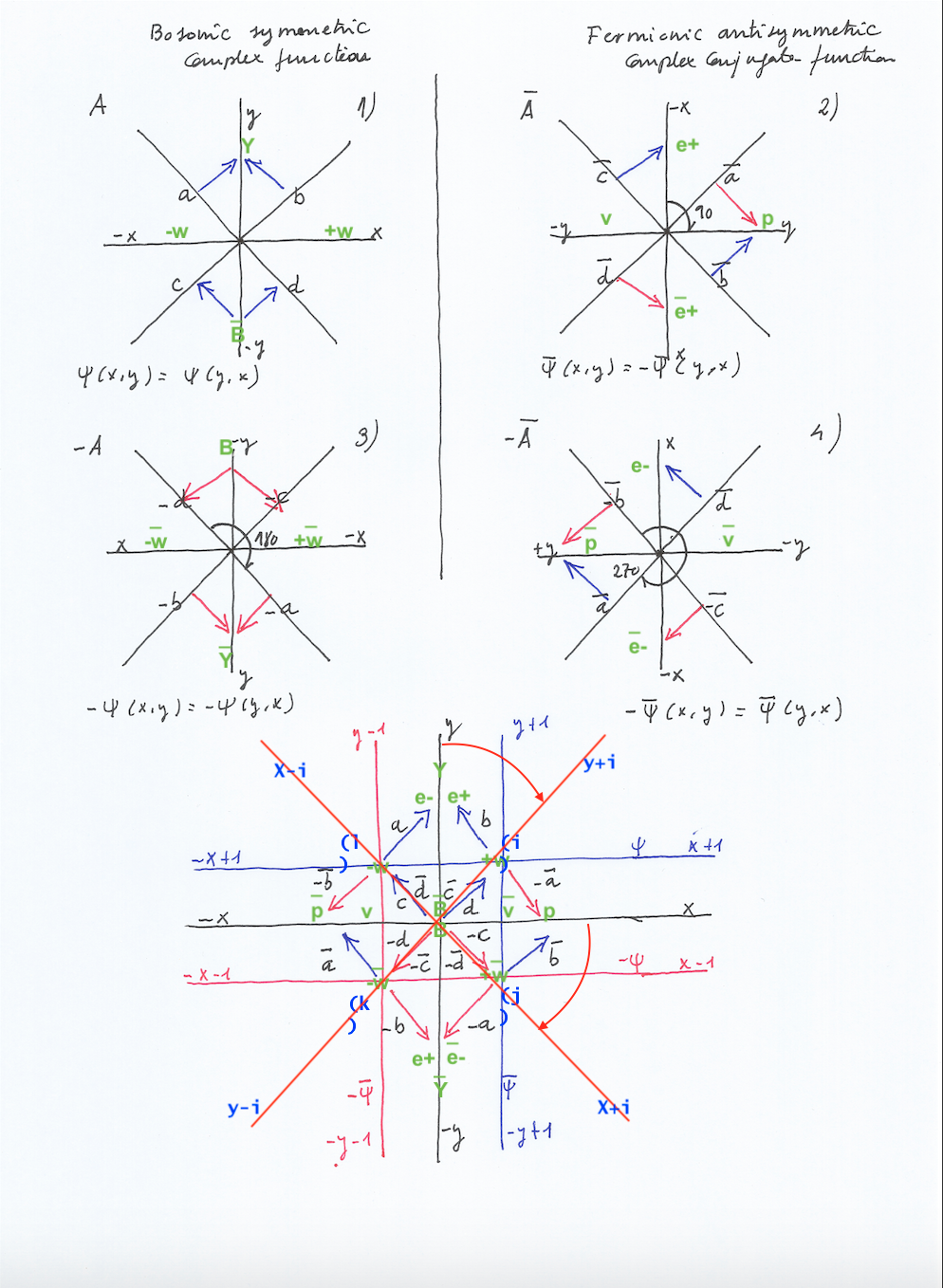
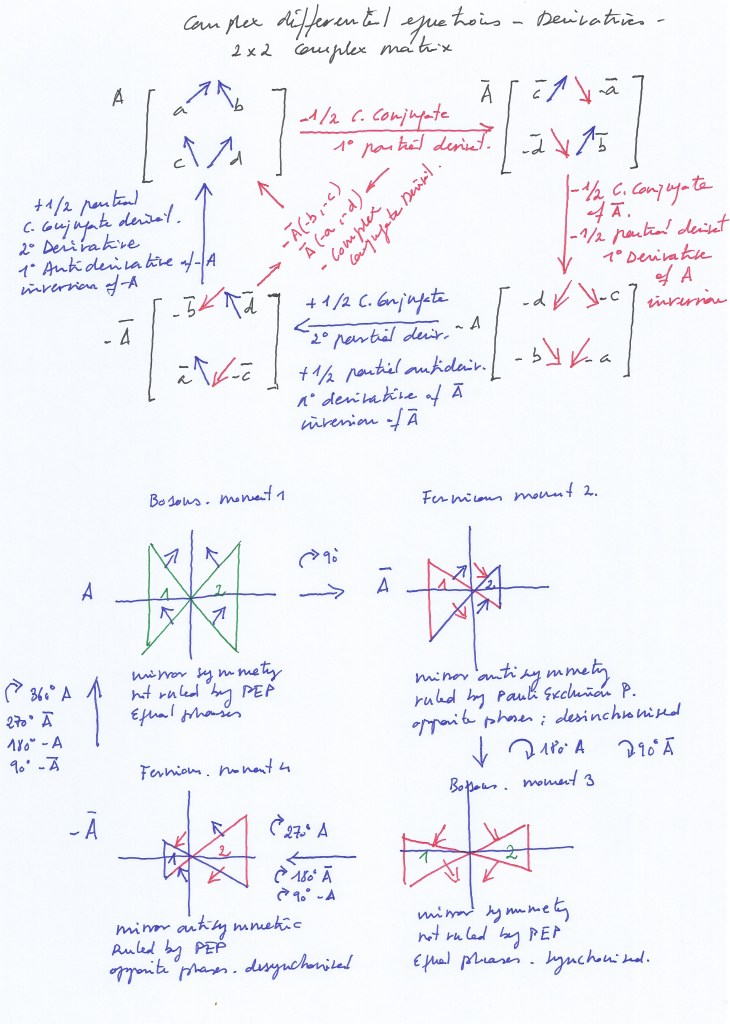
Each eigenvector has two possible directions, given by their positive or negative sign. In that sense, the antisymmetric system can be described by a complex conjugate function of two variables, and a pair of 2×2 complex matrices whose elements the mentioned eigenvectors:
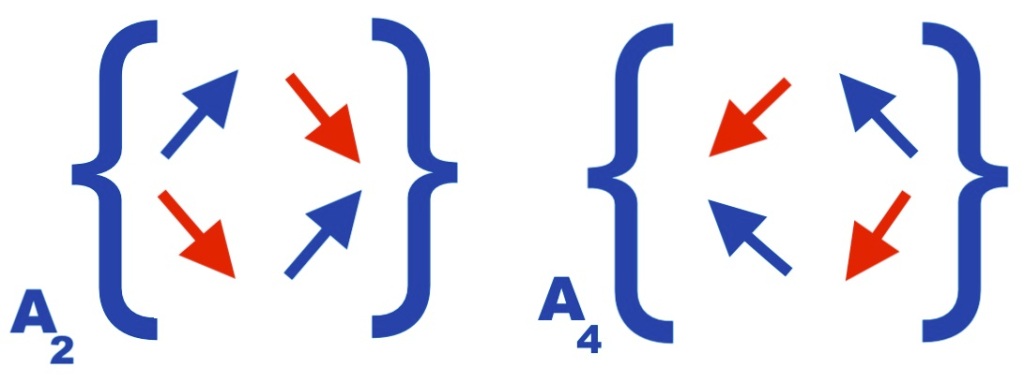
Fig. 2 represents the pair of 2×2 complex conjugate matrices of eigenvectors with eigenvalue 1 or -1 related to the antisymmetric system.
2. Symmetric system
In the symmetric system the two intersecting field vary with the same phase, they simultaneously contract and, later, they will simultaneously expand.
The transversal subfields, being isomorphic, exhibit chiral mirror symmetry at the same time. That implies that performing the inversion of the system, which would be equivalent to a 180 degrees rotation, both subfields would be interchangeable, and so the right and left transverse subfields would be mapped to the left and right transverse subfields.
However, considering the dynamics given by the periodic contraction and expansion of the intersecting fields, it can occur that when the contracting system with expanding transverse subfield is inverted, the curvatures of the intersecting fields have already change and so the transverse subfields are now contracting.
That would imply that the unrotated right expanding field would be mapped to the left rotated contracting subfield, and the left unrotated expanding subfield would be mapped to the rotated right expanding subfield.
In that way, the source and target subfields will not be isomorphic in the symmetric system.
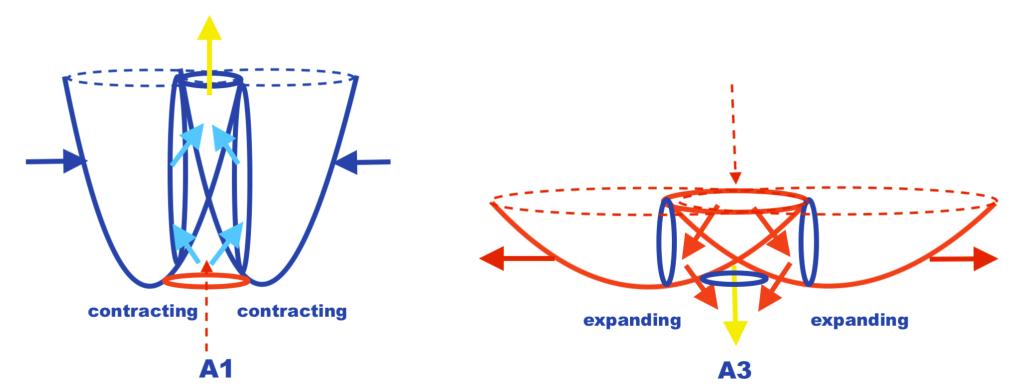
Fig. 3 Represents the two moments of the symmetric system. At moment A1, the right and left transverse subfields expand, exhibiting chiral mirror symmetry. Later, at moment A3, the right and left transverse subfield still exhibit chiral mirror symmetry, but as they are now contracting, they are not isomorphic with respect to the A1 subfields.
The evolution of the symmetric system can be described by a complex function of two variables, as the four eigenvectors only can have two possible directions, and a pair of 2×2 complex matrices of eigenvectors with eigenvalue 1 or -1:
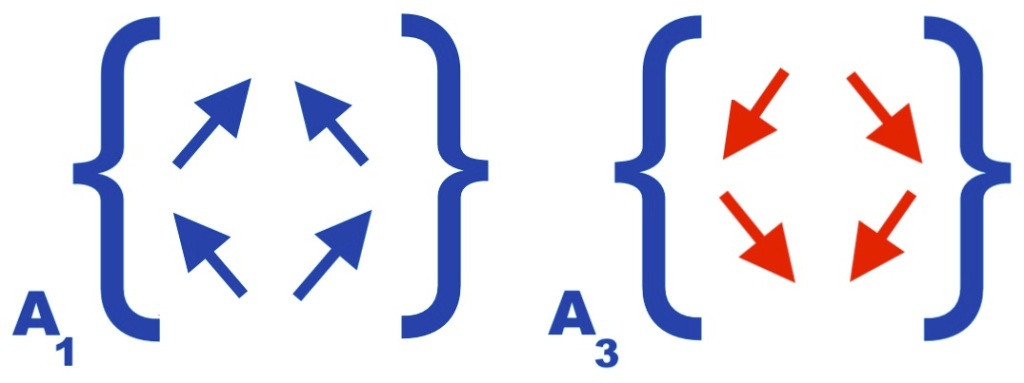
Fig. 4 represents the pair of 2×2 complex conjugate matrices of eigenvectors related to the antisymmetric system.
3. Rotational system.
So far, we have described the inversion that performs the mapping between the transverse subfields in terms of a symbolic 180 degrees rotation, where the symmetric and antisymmetric systems are considered as separate and unrelated systems described by a complex and a complex conjugated function of two variables, respectively.
However, in the context of a system that physically rotates, the symmetric and the antisymmetric systems may turn to be a same system that is topologically transformed after each 90 degrees rotation, becoming periodically symmetric or antisymmetric.
That implies that the evolution of the system must be described by two interpolated functions, the complex function, and its harmonic conjugate solution.
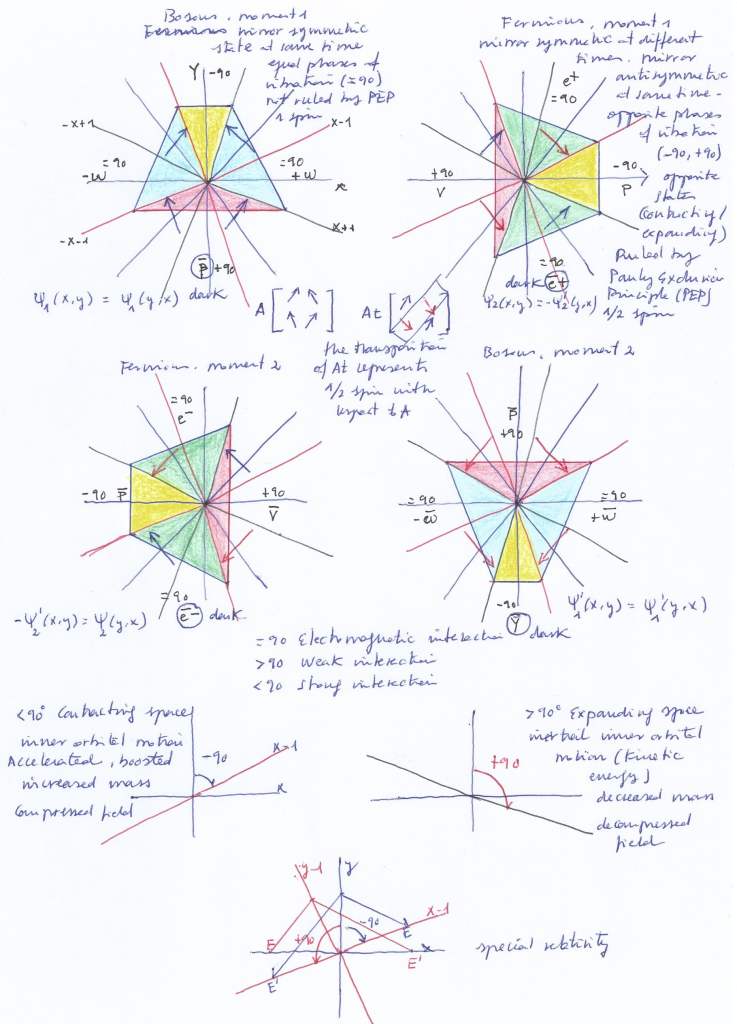
Fig. 5 Represents the rotational evolution of the system where its mirror symmetry gets periodically broken or restored, becoming antisymmetric or symmetric after each 90 degrees rotation.
The evolution of the rotational system can be represented by a set of 2×2 complex rotational 2 matrices of eigenvectors with eigenvalue 1 or -1:

Fig. 6 represents the set of 2×2 rotational matrices related by pairs to the complex symmetric (A1 and A3) and the conjugate antisymmetric (A2 and A4) systems.
Taking A2 as the identity matrix, the inversion operated at A4 mapping A2 implies a partial conjugation given by the 90 degrees rotation of A2 performed at A3. In that way, the two positive eigenvectors of A2 change their sign at A3. This operation can be interpreted as a ½ order derivative.
It also implies the transposition of A3, given by the partial conjugation operated at A4. Two of the negative eigenvectors of A3 become positive at A4. Their sign commutation can be interpreted as a ½ order antiderivative. In that sense, the first order differentiation that operates the inversion of the antisymmetric system will involve a ½ derivative and a ½ antiderivative.
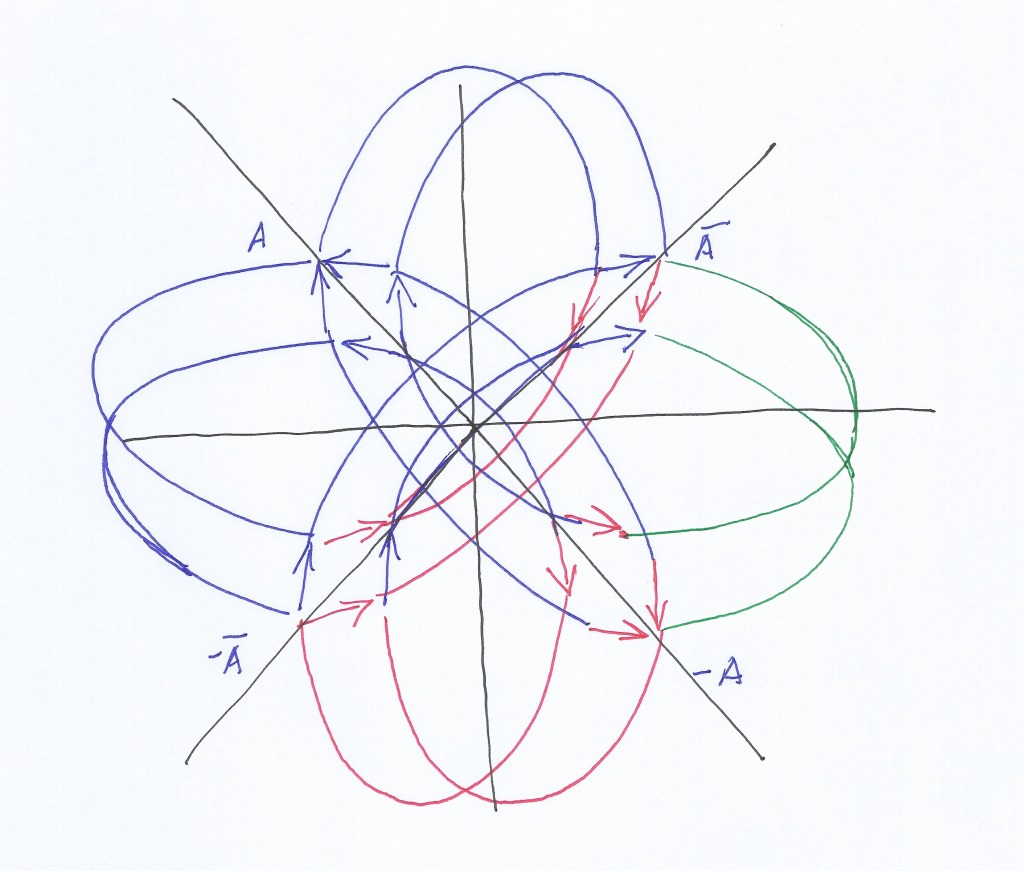
On the other hand, in the rotational system, the vectors do not simply change their sign by a 180 degrees permutation, they are physically rotated with the whole complex plane. Their change of spatial position can be observed if we identify them with letters.
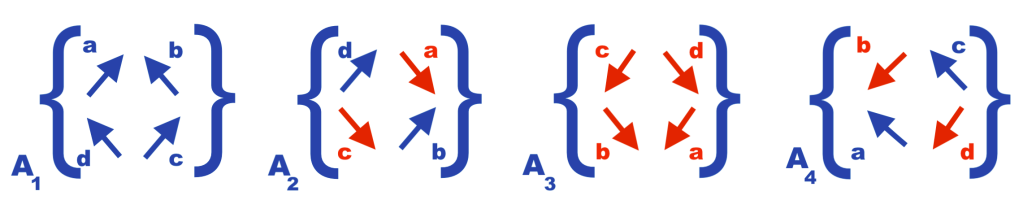
Fig. 7 Represents the actual rotation of the vectors in the context of the rotational matrices, changing their position after each 90 degrees rotation.
Considering them as eigenvectors, each of them only can have two possible directions. But considering them as rotational vectors, they will have four possible directions. In that sense, the interpolating rotational system must be thought as a four variables polynomial.
Considering A2 as the starting point, and performing its inversion, from the pint of view of the rotational vectors the number of variables would be three.
However, it does not seem possible to arbitrarily separate matrix A2 from matrix A1, as it is the transposition of matrix A1 by means of its partial conjugation what gives birth to matrix A2.
The inversion of A2 involves the transposition of A3, which is the negative reflection of A1. A2 is the first order (½ + ½) derivative of A1 and A1 the first order antiderivative (½ + ½) antiderivative of A3. A1 and A3 are intertwined to A2 and A4, and they all are interdependent.
4. Jacobian conjecture.
The Jacobian conjecture formulated by Keller [1] in 1939 states that if a polynomial map from an n-dimensional space to itself has Jacobian determinant which is a non-zero constant, then the function has a polynomial inverse.
Expressed in terms of vectorial functions, it would state that if a vector-valued function (or map) from an n-dimensional space to itself has Jacobian determinant which is a non-zero constant, then the function (or map) has a vector-valued inverse.
The Jacobian determinant is a measure of how much a transformation stretches or shrinks the space it maps to, and it is defined for continuous transformations. The Jacobian conjecture applies to maps between homeomorphic spaces, which are those that can be continuously deformed into one another.
In the context of the rotational system, the transformations are continuous but not in a linear way. The smooth continuity passes through the interpolation of the antisymmetric and the symmetric systems after each 90 degrees rotation.
In that way, the topological structure of the transverse subfields is preserved, being automorphic, even when their size is not identical as it happens in the symmetric system when the contracting subfields map the expanding subfields. Their curvatures are always half positive and half negative, as they are formed by the inner curvature of an intersecting field and by the outer curvature of the other intersecting field.
In the antisymmetric system, the topological structure of the automorphic vertical subfield that maps to itself when moving leftward or rightward is also preserved because it’s always formed by a negative curvature formed by the inner curvatures of both left and right intersecting fields.
In the case of the symmetric system, the top vertical subfield that moves upward while contracting when the two intersecting fields contract, has a negative curvature. However, when that vertical subfield decays moving downward while expanding, when both intersecting fields expand, the inverse subfield that maps the previously ascending subfield is placed in the convex side of the system having a double positive curvature.
In that sense, the topological structure of the concave vertical subfield is not preserved in the inverse convex subfield. But, still, the ascending contracting concave subfield can be considered mapped to itself when a moment later descends while expanding. However, in that case the mirror reflection property of the vertical subfield would not be considered by the conjecture.
The set of transformation matrices result from the operations of transposition, complex conjugation (as the sum of two partial complex conjugations), and inversion.
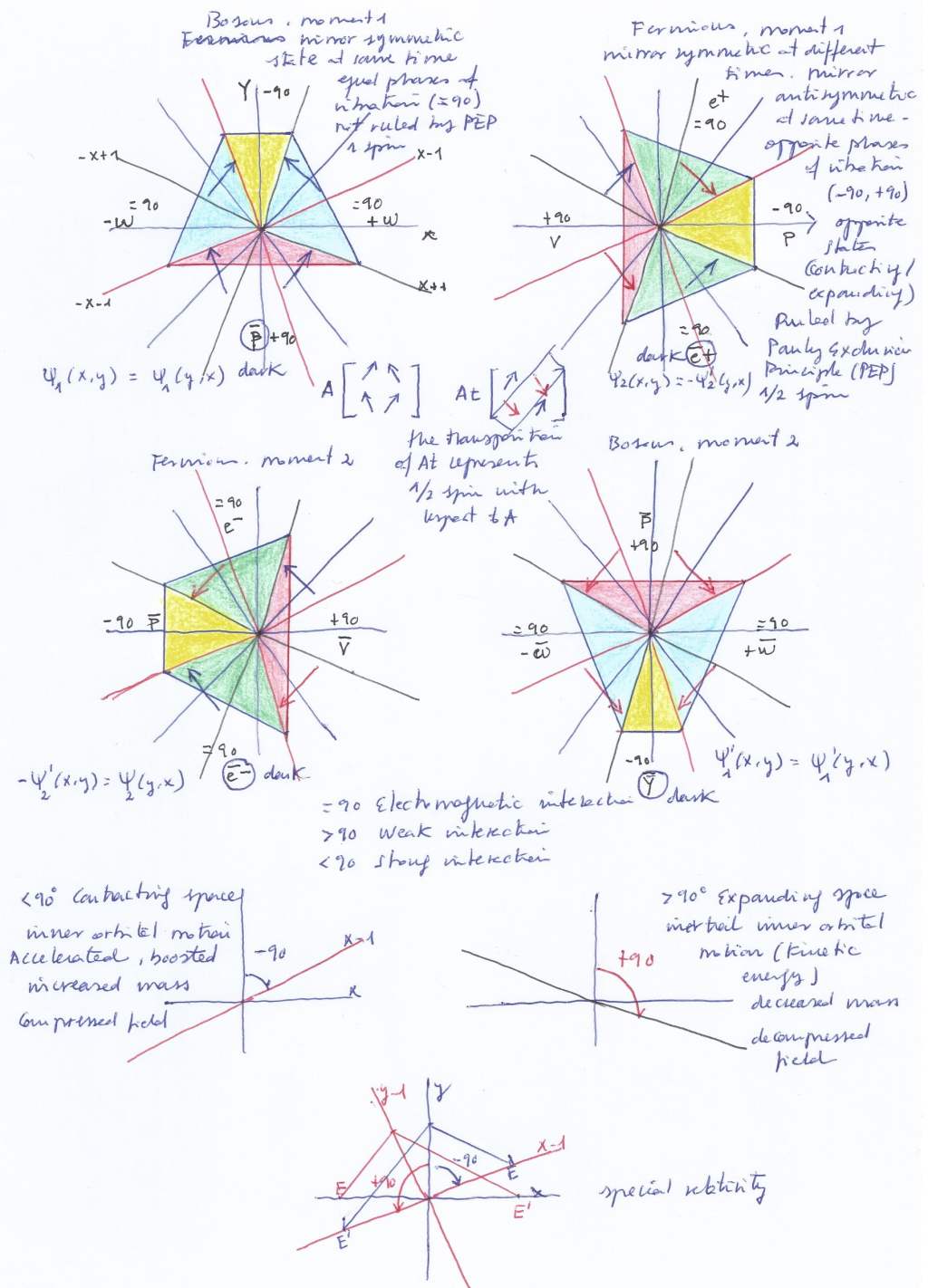
- A1 (0-degree rotation) represents the eigenvectors in the symmetric system, when the transversal subspaces have mirror symmetry at the same moment; performing its partial conjugation (rotating the plane 90-degree) only two eigenvectors (acting as two variables) change their sign at A2.
- A2 (90-degree rotation) represents the eigenvectors when half of the system has a delayed its phase, introducing a purely imaginary time dimension) having mirror antisymmetry with respect to the other half side. A2 represents a ½ order derivative of A1.
- A3 (180-degree rotation) represents the partial conjugation of A2 (only the yet two uncommuted eigenvectors commute now their sign with respect to A2); A3 also represents the negative reflection of A1; its four eigenvectors (acting as four variables) have already commuted their sign with respect to A1; A3 represents the ½ order derivative of A2, and the first order (½ + ½) derivative of A1.
- A4 (270-degree rotation with respect to A1, 180-degree with respect to A2, and 90-degree with respect to A3) represents the transpose of A3, the ½ order antiderivative of A3, the second transposition of A1, and the first order (½ + ½) derivative of A2; A4 is also the negative mirror reflection of A2, having commuted their sign the four eigenvectors.
- An additional 90-degree rotation produces A1 which represents the positive reflection of A3, a ½ order antiderivative of A4, and the first order (½ + ½) antiderivative of A3
5. Sobolev interpolation.
The interpolation of the function spaces can be interpreted in terms of Sobolev interpolations [2], Sobolev inequality and Sobolev embedding. It is graphically represented in Fig. 8:
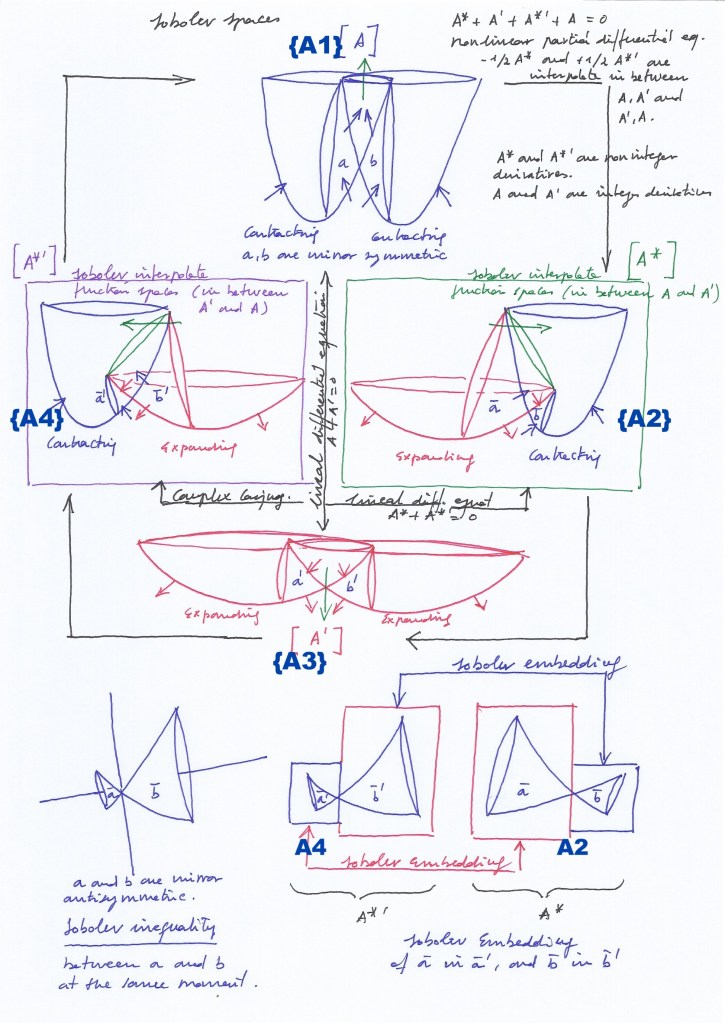
The interdependence of the complex and the conjugate functions complex and conjugate functions given by their mutual interpolation, and their relation to the vector matrices can be represented graphically in Fig. 9:
6. Operational Algebras.
Considering the rotational fields system as a specific case of the Jacobian conjecture, it is possible to conceptually infer its possible relations to Tomita-Takesaki (TT) modular theory [3].
In TT theory two intersecting algebras form two shared “modular inclusions” (with + – half sided subalgebras) and a “modular intersection” (with an integer sided subalgebra).
The left and right half handed subalgebras will be images of each other, when they are commutative, or they will not be their mirror image when they are noncommutative.
Mapping the modular inclusion to its reflection image, the left and right subalgebras will be the opposite image of each other (reverting their initial signs) if they are commutative; if they are noncommutative, the initial left sided subalgebra will be the image of the right sided mapped subalgebra, and the initial right-handed subalgebra will be the image of the left sided mapped subalgebra.
TT theory decomposes a linear transformation into its modular building blocks, revealing its automorphisms.
Decomposing the bounded operator, it obtains the modular operator and the modular conjugation (or modular involution) which is a transformation that reverses the orientation, preserving distances and angles.
Translating the abstract algebraic terms to the fields model, two intersecting algebras would represent the two intersecting fields fluctuating with the same or opposite phase.
The half handed subalgebras (or “modular inclusions”) will be the transversal subfields of the nucleus shared by the intersecting fields, while the integer handed subalgebra (or “intersection inclusion”) will be our vertical subfields. In this context, we identify commutativity and noncommutativity with mirror symmetry and mirror antisymmetry, respectively.
The bounded operator that is decomposed will be the 90-degree rotational matrix; The modular building blocks are the set of matrices that are obtained when applying the operator.
The modular operator will be the ½ partial conjugate A2 matrix; And the modular conjugation will be the conjugate matrix A4, which forms the whole conjugation by adding the fractional conjugations ½ + ½.
Therefore, by separating the conjugate matrix from the complex one the automorphism of the antisymmetric conjugate system is found.
The half sided algebras that form a modular inclusion are noncommutative, it means we are in the antisymmetric system where the left intersecting field contracts while the right one contracts and vice versa; in that system, the left transversal subfield will be the mirror symmetric image (it will be the mapped image) of the right transversal subfield when, later, the left intersecting field expands and the right one contracts.
In that sense, a past half handed subalgebra is being mapped with its future image. A time delay will exist between both subalgebras.
Considering Δ as the modular operator A2, J the modular conjugation A4, and M the intersection of two Von Newmann algebras, Δ^-Yt M Δ^it will represent the positive and negative ½ sided modular inclusions of the modular operator, being t a real time dimension and it an imaginary time dimension given by the partial conjugation of A1 or A3.
It is this different time dimension what makes noncommutative, as non-interchangeable, the modular + and – inclusions related to Δ in the antisymmetric system.
Applying the modular involution, yields J^yt M’ J^-it.
Δ^-yt is transformed into J^ytand Δ^it is transformed into J^-it’, being J^yt M’J^-it the involutive automorphism of Δ^-ytM Δ^it.
The noncommutative, as non-interchangeable, Δ^-yt and Δ^it become commutative or interchangeable through time at J^yt M’ J^-it, fixing their antisymmetry in that way.
The same type of operations can be performed by taking A2 as the identity matrix. Rotating clockwise, A3 would be the modular operator and A1 the modular conjugate automorphism.
7. Reflection positivity
Related to the delay in time in the antisymmetric system, it can also be mentioned a property that all unitary quantum field theories are expected to hold: “reflection positivity” (RP). [4]
The positive increasing energy that appears in one side of the mirror system should also be reflected in the other side. However, in the context of the antisymmetric system, the positive or increasing energy of the contracting right transverse subfield does not mirror simultaneously in the expanding left transverse subfield, which exhibits negative or decreasing energy.
Therefore, to obtain a positive energy reflected at the left side, making the sides of the system virtually symmetric, a time reversal operation is needed.
To observe the positive energy reflected at the left side, it will be needed to go back in time to the moment where the left transversal subfield was contracting and had a positive energy. This operation is performed by a type of “Wick rotation”. [5]
The main time phase of the symmetric system can be represented with the Y coordinate.
By performing a partial conjugation that involves a fractional derivative, the time coordinate Y undergoes a rotation into the purely imaginary dimension within the complex plane. At that moment, the mirror system becomes antisymmetric as one side of the system keeps following the imaginary time of Y while the other side follows a harmonic phase. A positive or negative time lag has been introduced.
Reversion time on one side of the system serves as a symbolic tool to virtually restore symmetry to the time phases. To revert to the previous time, one could perform a reverse rotation of the complex time axis (X +iY) to achieve a full complex conjugation at (–X –IY).
In the A matrices context, that time backwards rotation represents an antiderivative of -A.
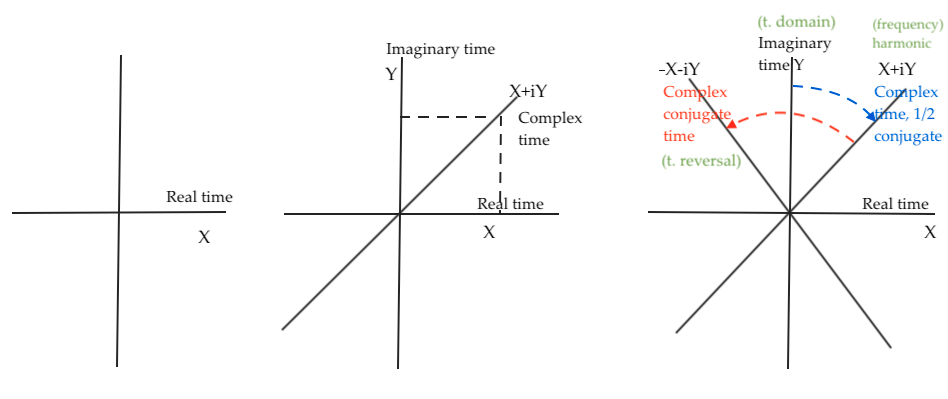
Fig. 10 Rotational time backwards and forwards
When the time reverse has been symbolically completed, in the left side of the mirror system the left subfield will be contracting, having an increased positive energy; this is a past reflection of the future positive energy that there will be a moment later in right side.

Fig. 11 Reflection positivity in the antisymmetric system
In the reverse past time, at the right side of the system the right subfield will be expanding having a decreased negative energy.
In regard to the symmetric system, positivity is reflected between the right and left transverse subfields at the same time. In that sense, it’s not necessary to use the Wick operation to reverse time.
Both left and right transversal subfields will be the mirror reflection of each other at the same time. However, in the case of the strong interaction in the symmetric system, when the contracting vertical subfield has an increased positive energy while ascending to emit a pushing force, it will be necessary to virtually visit a past moment to look for a previous state where positivity could be reflected.
Going back in time, the vertical subfield will be losing its energy while expanding, moving downwards. Therefore, at that past moment, the vertical subfield will not display a positive energy.
Reflection positivity, however, can be found at that past moment in the convex side of the system of the two intersecting fields, where an inverted subfield with convex curvatures will be experiencing an increased energy.
That inverted subfield can mirror the vertical subfield which in a future state will be ascending in the concave side of the system through the Y axis.

Fig. 12 Reflection positivity in the symmetric system
The missing reflection positivity in the concave side of the system in the strong interaction can be related to a mass gap problem when it comes to the weak interaction.
8. Mass gap problem
There will be a mass gap [6] in the system when the two intersecting fields simultaneously expand, and the vertical subfield experiences a decay of energy.
This case represents the ground state with the lowest possible energy of the vertical subfield, which is always greater than 0 because the highest rate of expansion of the intersecting fields prevents them from having zero curvature.
The zero point of the vacuum, where there should be no energy nor mass, is placed at the point of intersection of the XY coordinates, and that point is never reached by the vertical subfield that descends through the Y axis while expanding during its decay.
An “upper” mass gap would be referred to the highest possible mass of a particle in the strong interaction. Its limit would be given by the greatest rate of contraction of the intersecting spaces.
Fig. 12 represents graphically the mass gap in the symmetric system; the upper gap occurs in the compressed photonic subfield when both intersecting fields contract, while the lower gap occurs in the decompressed subfield when both intersecting fields expand:
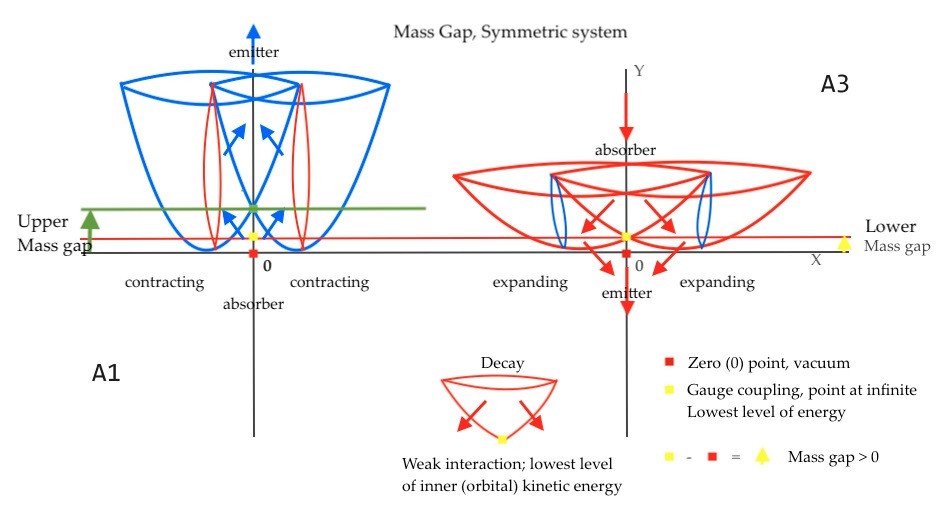
Fig. 13 Mass gap in the symmetric system
The zero point of the vertical subfield is marked in yellow on the above diagram, at the point of intersection of the left and right intersecting fields.
The gap is given by the distance from that point to the zero point where the X and Y coordinates intersect, represented by a red mark. An arrow shows the gap distance between those critical points.
However, in this model, the zero point does not represent a vacuum where neither energy nor mass exists.
When the mass and energy of the vertical subfield reach their weakest level in the concave side of the symmetric system, an equivalent amount of energy and mass arises in the convex side, where the zero point is located, as the result of the double pushing force caused by the displacement of the positive curvature of the expanding intersecting fields.
That mass and energy at this zero point will be considered dark from the point of view of the concave side of the system.
In the antisymmetric system, the lowest energy level occurs when a transverse subfield experiences a double decompression due to the displacement of the concave curvature of the contracting intersecting field and the displacement of the positive curvature of the expanding intersecting field.
The corresponding double compression is then experienced by its mirror antisymmetric transverse subfield.
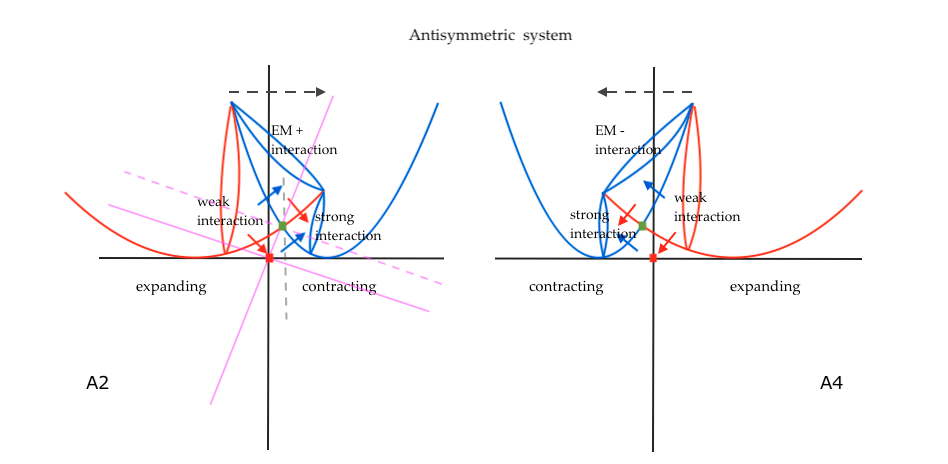
Fig. 14 Represents visually the map gap in the antisymmetric system, with the left and right displacements of the point of intersection:
Fig. 14 Mass gap in the antisymmetric system
9. T-Duality and SYZ conjecture.
As it has been showed before, in the antisymmetric system the transverse subspaces periodically change their role becoming the negative or positive reflection of each other at different times.
This type of automorphic mirror reflection symmetry at different times may be related to the SYZ conjecture [7] in String theory, which states that there exists a special type of Calabi-Yau manifold that is related to another Calabi-Yau [8] manifold by a T-duality transformation.
In string theory, mirror symmetry emerges from the notion of T-duality [9], that relates the spaces described by Type IIA and type IIB strings theories.
In Type IIA string theory, the strings can move freely in the Calabi-Yau transverse space with a larger radius, while in type IIB string theory, the strings are confined to the boundaries of the transverse space of shorter radius.
T-duality relates these two different types of larger and smaller transversal spaces by means of a type of inversion that exchanges the roles of the large and small radii transverse spaces.
In the context of the dual fields model, the Calabi-Yau spaces of smaller or larger radius may be considered equivalent to the transverse contracting or expanding subspaces that are mapped to each other in a mirror symmetric way by means of their topological transformation through time, as described before in the antisymmetric rotational system.
The elliptic orbits inside of the transversal subfields, caused by their periodical expansion and contraction, can be visually related to the notion of elliptic fibrations used in String theories.
Fig. 15 represents the elliptic fibrations as the inner orbits in the transverse subspaces of the antisymmetric system.
10. Theoretical Quantum field model with an exotic nucleus
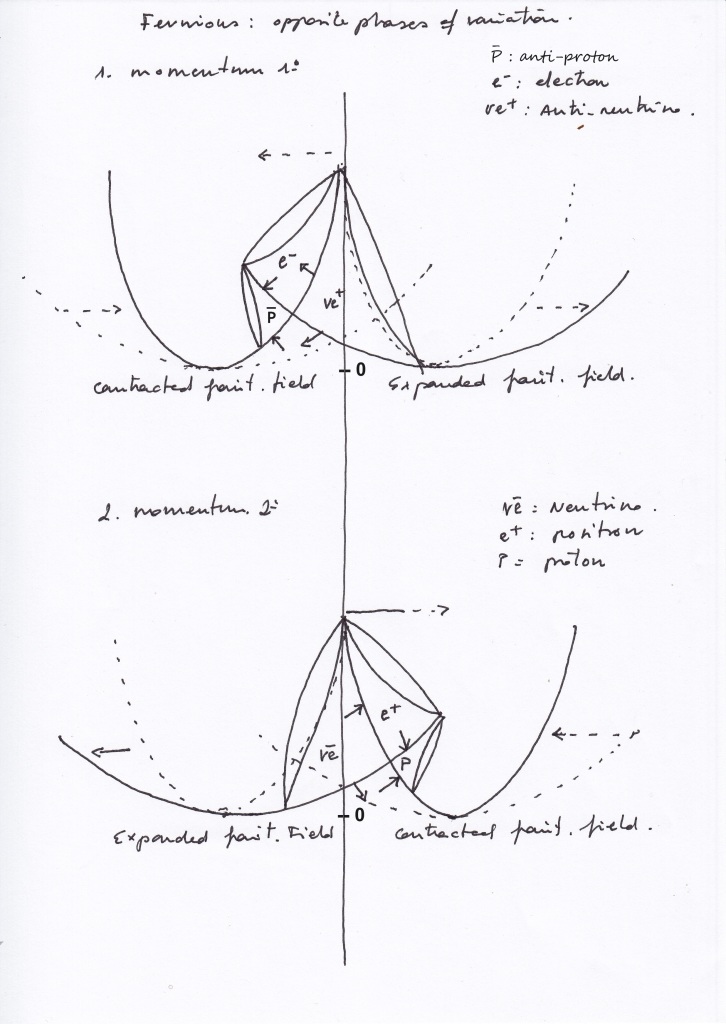
The fields model emerges in the context of the development of a supersymmetric quantum field model of an atom formed by the two intersecting fields that share a nucleus of two transvers and two vertical subfields that represent the matter and antimatter of the dual structure [10].
The composition of the atomic antisymmetric nucleus will depend on the specific moment of the system’s evolution. It may consist of a proton, a positron and a neutrino, or an antiproton, an electron, and an antineutrino.
10.1 Antisymmetric system, the left intersecting field expands while the right one contracts (A2)
- The right contracting transversal subspace will represent a proton.
- The left expanding transversal subspace will represent a neutrino.
- The vertical subspace moving toward the right will represent a positron.
10.2 Antisymmetric system, the left intersecting field contracts while the right one expands (A4)
- The right contracting proton will expand, becoming a right expanding antineutrino.
- The left expanding neutrino will contract, becoming a left-handed contracting antiproton.
- The vertical positron will move toward the left, becoming an electron.
Fig. 16 visually represents the limit states of the evolution of the antisymmetric system.
However, it does not reflect the moment when the top vertical subfield passes through the central axis, which is the reference center of symmetry of the system, carrying a neutral charge.
It is considered neutral because it is placed in the location used to distinguish between positive or negative: from that central point to the right the charge will be positive, and from that point to the left it will be negative.
This neutrality will occur during the intermediate expansion or contraction of the intersecting fields.
In that case, the proton (or antiproton) transversal subfield, and the neutrino (or antineutrino) transversal subfield will show an isomorphic shape and their positive and negative charges will be in compensation. It may be at that moment when the notion of neutron and antineutron arises.
Fig. 15 shows how the right-handed proton at moment A2 will decay, being virtually embedded in a right-handed antineutrino at moment A4, both in the right side of the mirror system.
Simultaneously, in the left side of the antisymmetric system an antiproton and an electron arise.
Later, the left-handed antiproton of A4 will decay into a left-handed neutrino at A2, while in the right side of the mirror system a proton and a positron will arise.
Proton and antiproton, and neutrino and antineutrino, will be Dirac antiparticles at different times.
Positron and electron are the same subfield, acting at different times as their own mirror reflection Majorana antimatter.
The existence of an electron and a positron in the same atom, also known as “positronium” [11], was predicted by Dirac in 1928. However, positronium was formulated as an exotic atom with no proton in its nucleus.
The coexistence of proton and antiproton in the same atom is currently accepted as an exotic structure called “protonium” [12] with no electrons nor positrons.
In the dual atomic model, matter and antimatter coexist and are relate to each other by means of their chiral mirror reflection symmetry at the same or different times.
All the subfields in the antisymmetric system are fermions with noninteger ½ spin, represented by the commuted eigenvector, being ruled by the Pauli exclusion principle. In that regard, they should adhere to Fermi-Dirac statistics, although the dual atomic nucleus is a causal model that can be described without using probability.
Additionally, in that same context, considering an antisymmetric Schrödinger’s cat as a figurative example, it could be said that the right alive contracting cat will be the delayed reflection of the left dead expanding cat, and vice versa.
It can be discussed whether they are the future or the passed reflection of each other, but that will only be a way to speak.
There will not be a single alive and dead cat, but two identical cats with opposite states and positions.
Their simultaneous states of being “alive” and “dead” can be considered “superposed” but in the context of their mirror antisymmetry.
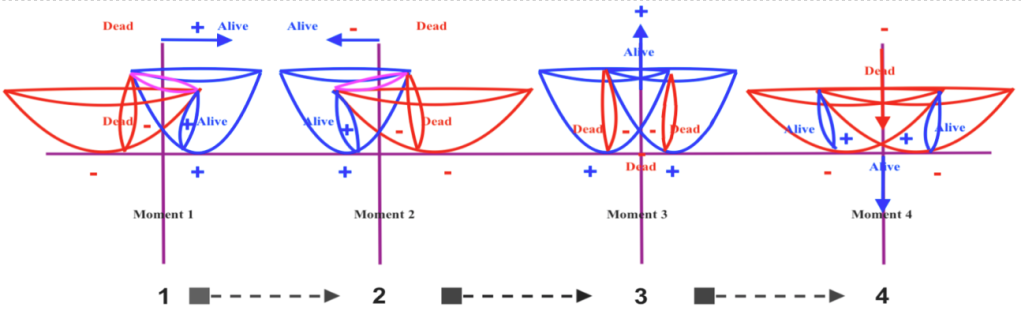
Fig. 17 MirrorSchrodinger “cats”without considering the rotational interpolation.
10.3 Symmetric system, when the left and right intersecting fields contract (A1)
- The right and left expanding transversal subspaces represent a right-handed positive and a left-handed negative gluon.
- The top vertical ascending subspace that contracts receiving a double force of compression will be the electromagnetic subfield that emits a photon while pushing upward.
- The inverted bottom vertical subspace at the convex side of the system represents the dark decay of a previous dark antiphoton.
10.4 Symmetric system, when the left and right intersecting fields expand (A3)
- The right and left expanding transverse subspaces may represent -W and +W bosons.
- The top vertical descending subspace will be the electromagnetic subfield losing its previous energy, after having emitted a photon.
- The bottom vertical subspace at the convex side of the system is the dark anti electromagnetic subfield that emits a dark antiphoton.
It can be visually observed in Fig. 17 that the left and right transversal subspaces will be mirror symmetric antimatters at the same time, being bosons not ruled by the Pauli exclusion principle. They should then obey the Fermi-Dirac statistics.
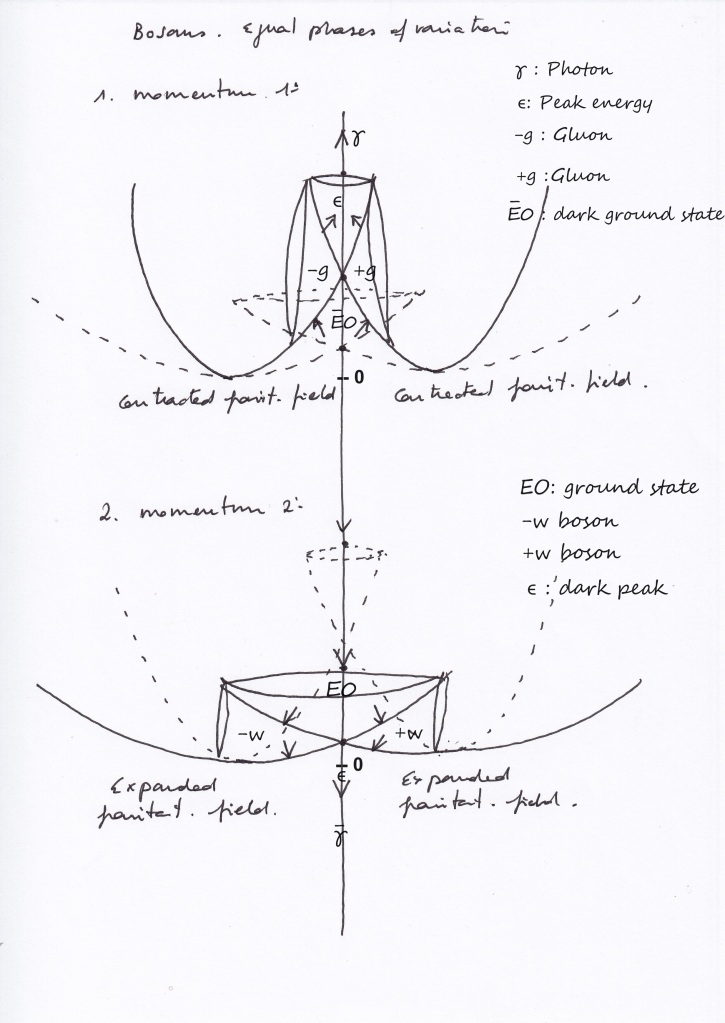
Fig. 18 Visually represents the limit states of the evolution of the antisymmetric system.
However, the photon and the dark antiphoton – or the vertical subfield from which they emerge –are mutually exclusive. Therefore, they are governed by the Pauli exclusion principle, even though they have an integer spin represented by the two converging eigenvectors.
The identity of the symmetric transversal subfields, labeled before as “W bosons” and “gluons” requires further clarification.
Each of those subfields receives a bottom inward pushing force and a top outward decompression – in the strong interaction – or a top inward pushing force and a bottom outward decompression – in the weak interaction.
In the strong interaction, the magnitudes of the pushing forces caused by contracting or expanding intersecting fields will be different, because the contracting field exhibits a higher density, intensifying the propulsive force caused by the displacement of its negative curvature.
The vertical photonic subfield receives an inward double pushing force from right to left and from left to right caused by the displacement of the negative curvatures of the intersecting fields.
These pushing forces are the same as those that decompress the transversal subfields – labeled as gluons – at that moment. The emitted photon would have a double helix spin. The pushing forces received at different moments by the moving right positron and the moving left electron in the antisymmetric system, now converge simultaneously in the photonic subfield.
From the perspective of this model, the transversal subspaces are the same topological subfields that contract when the intersecting fields expand in the weak interaction or expand when the intersecting fields contract in the strong interaction.
The strong and weak interactions, then, are related by the same mechanism. And the mirror transversal subfields that mediate the strong and weak interactions are the same topological subspaces that are transformed through time.
The model is N=1 because it relates in a supersymmetric way, through time, each fermionic subfield of the antisymmetric system with a bosonic subfield of the symmetric system.
In that way:
- The fermionic electron-positron subfield will be the superpartner of the bosonic vertical subfield that emits the photon when ascending.
- The fermionic proton-antineutrino subfield, and the fermionic antiproton-neutrino subfields will be the superpartners of the symmetric transversal right and left subfields respectively, when they contract or expand.
The symmetry of the system is preserved through time. The modular Hamiltonian of the system also remains invariant through time.
10.5 Geometric approach:
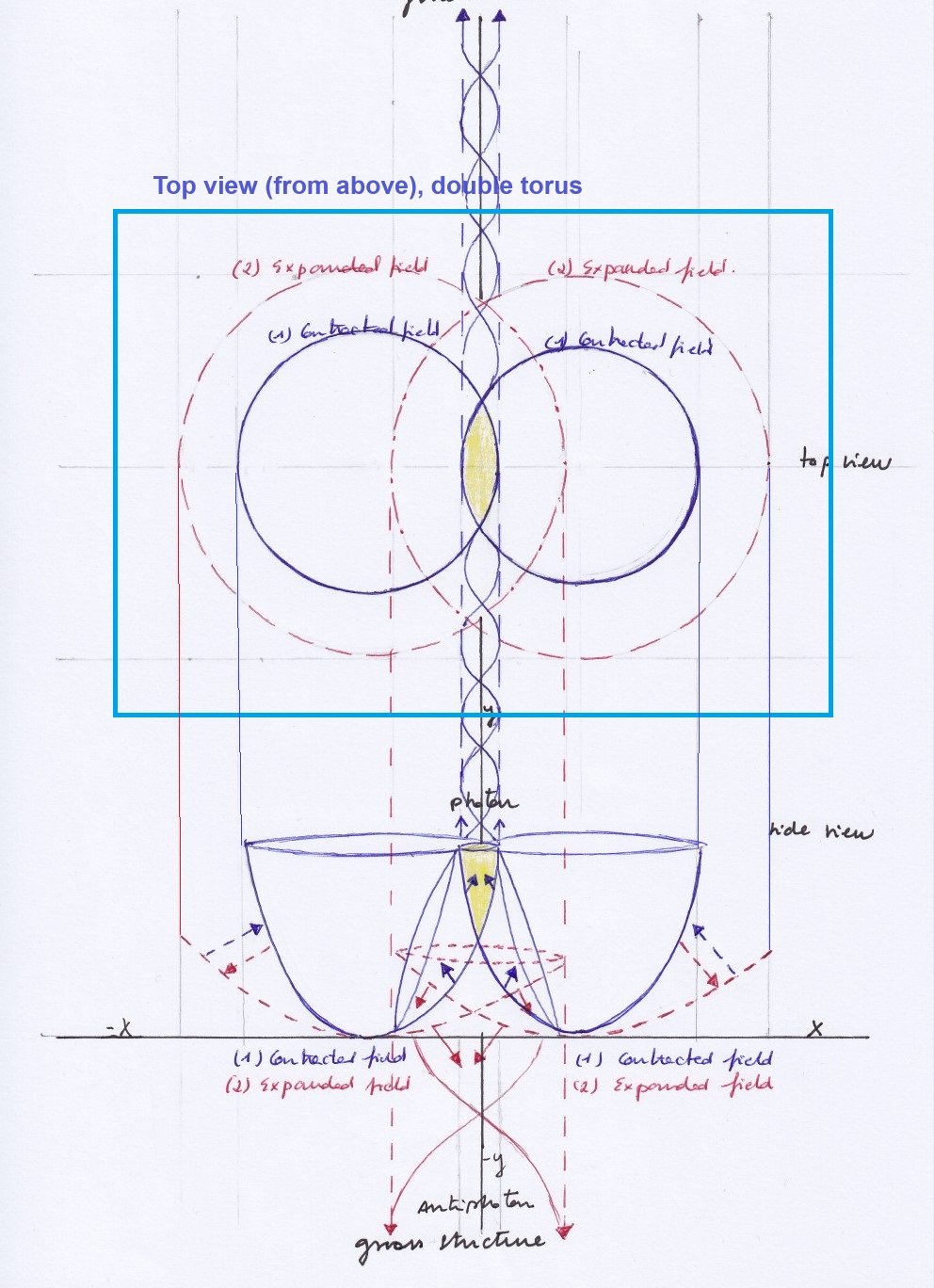
The intersecting spaces model can also be thought in terms of the topology of a two genus torus or two related tori.
The outer positive and the inner negative curvatures of the torus can be seen as the simultaneous representation of the expanding or contracting moments of the vibrating fields when looking at them from above, in an orthographic projection represented in Figs. 18 and 19.
The symmetric and antisymmetric subfields can be described as cobordant [13] subspaces. The vertical subspaces share borders with the left and right transversal subspaces, and they all share borders with the two intersecting spaces. These borders can be thought of as unidimensional lines described by the curvatures of the intersecting fields.
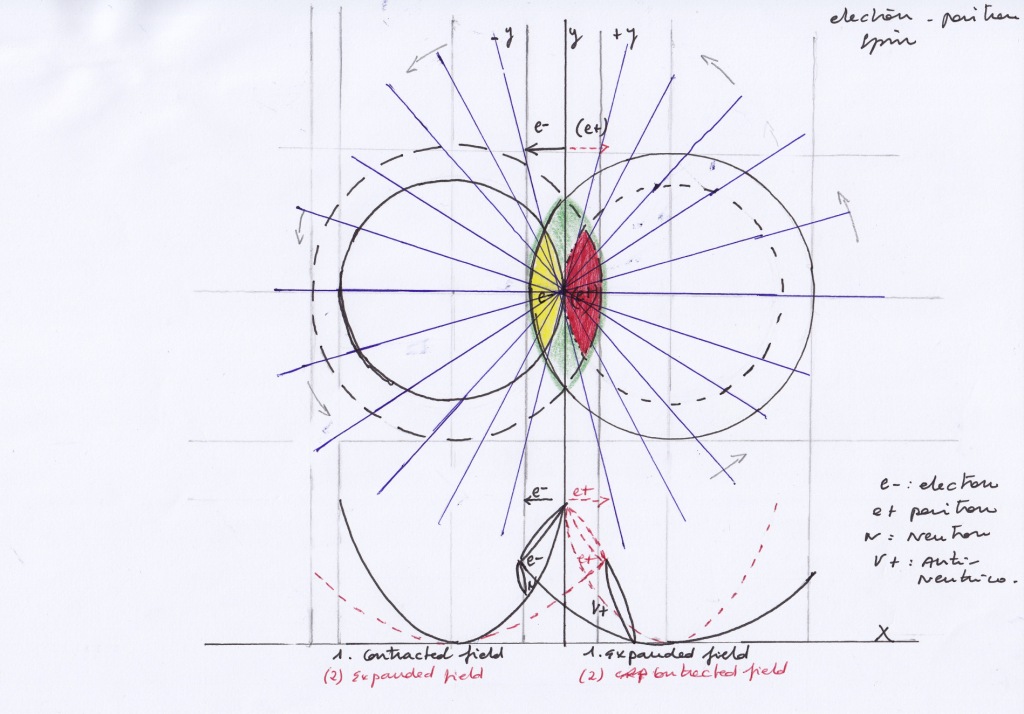
Fig. 19. Two genus torus projection of the antisymmetric system
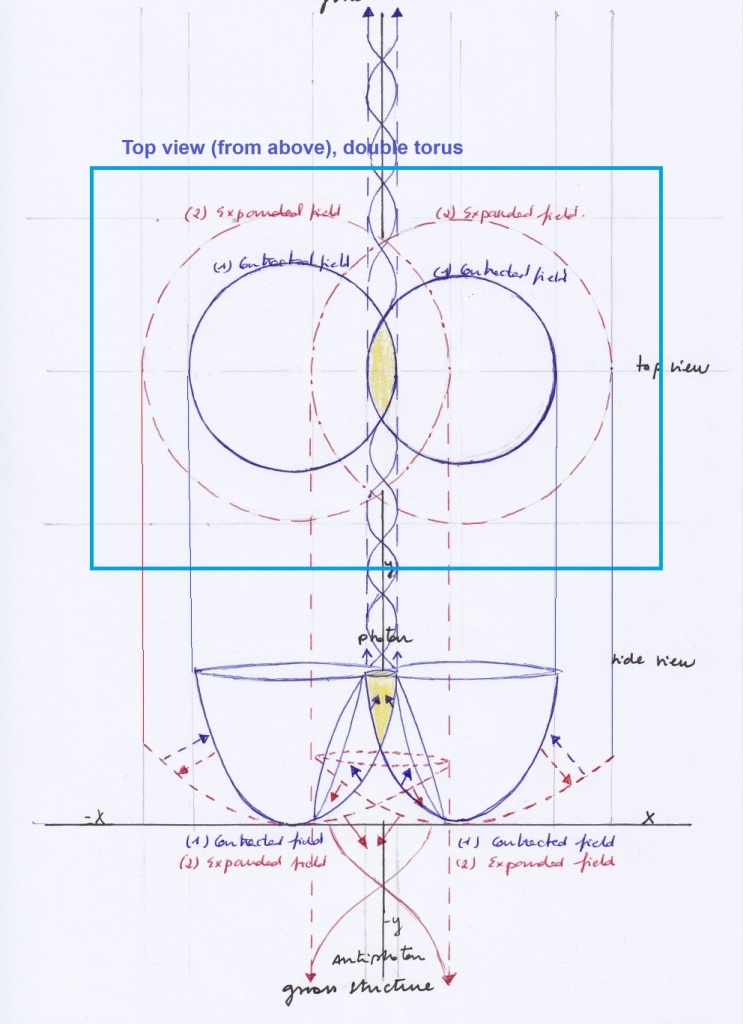
Fig. 20. Two genus torus projection of the symmetric system
11. Additional diagrams:
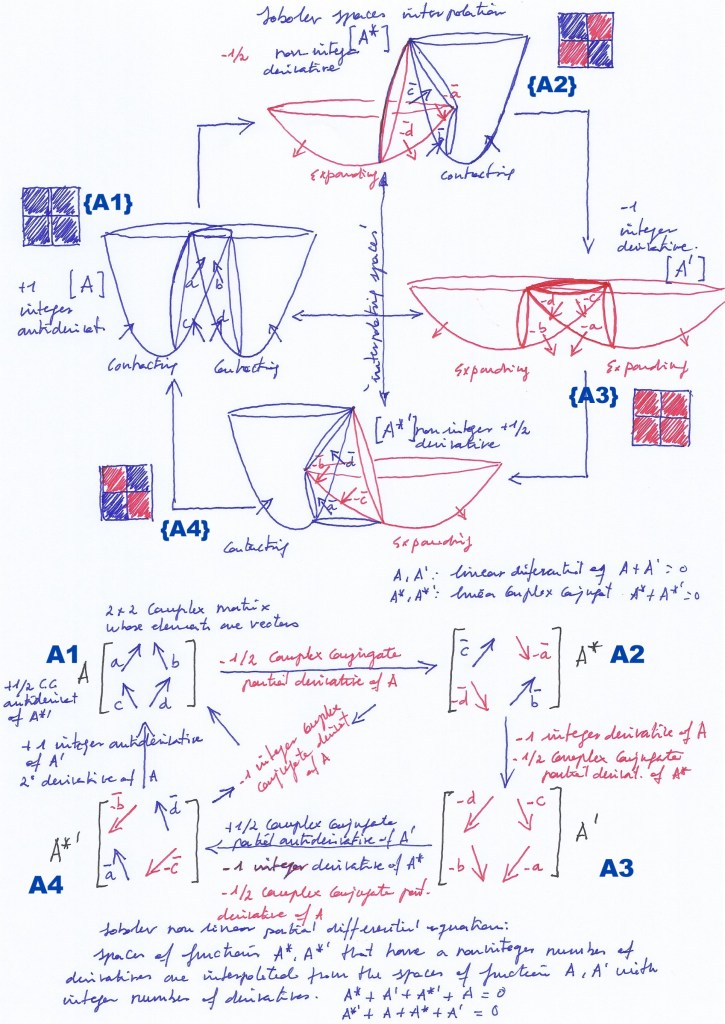
Fig. 21 Vector spaces interpolation
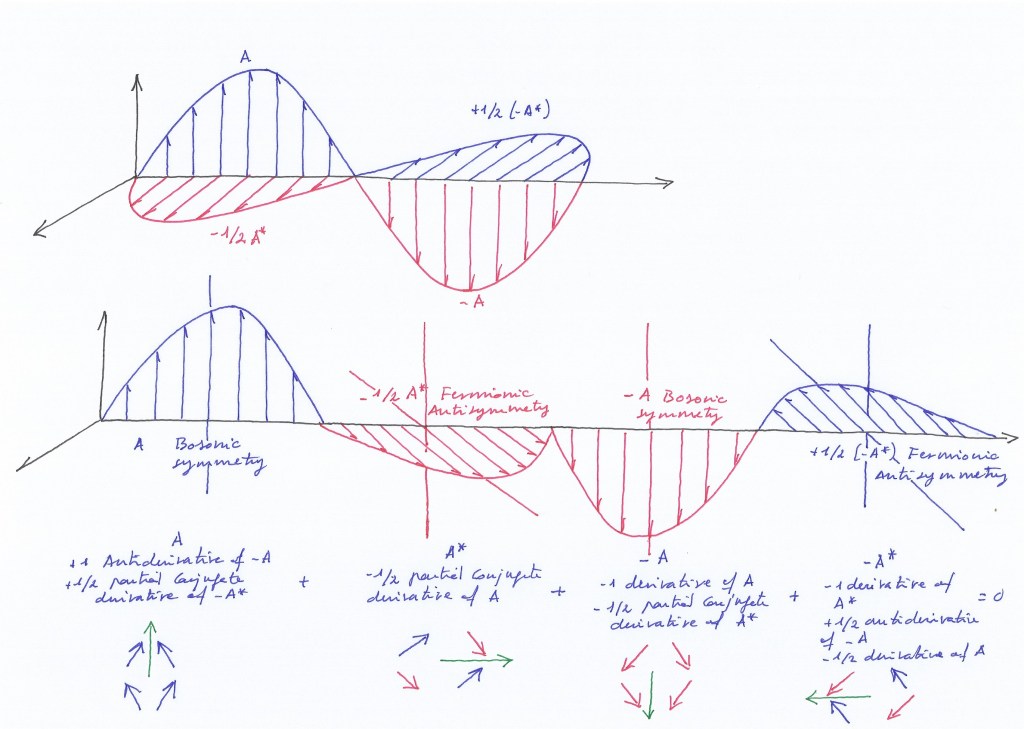
Fig. 22 Symbolic representation of the interpolated symmetric and antisymmetric systems as the electric and magnetic moments, respectively, of the rotational supersymmetric system.
12. References.
[1] Jacobian conjecture: https://en.wikipedia.org/wiki/Jacobian_conjecture
[2] Sobolev interpolation: https://en.wikipedia.org/wiki/Interpolation_space
[3] Tomita Takesaki Theory: https://en.wikipedia.org/wiki/Tomita E2 80 93Takesaki_theory
[4] Reflection positivity: https://www.pnas.org/doi/pdf/10.1073/pnas.1710707114
[5] Wick rotation: https://en.wikipedia.org/wiki/Wick_rotation
[6] Mass gap problem: https://en.wikipedia.org/wiki/Yang E2 80 93Mills_existence_and_mass_gap
[7] SYZ (Strominger, Yau, and Zaslow) conjecture: https://en.wikipedia.org/wiki/SYZ_conjecture
[8] Calabi-Yau transversal space: “The Shape of Inner Space” by Shing-Thu Yau” and Steve Nadis. Pp. 12-15. ISHN-10 0465020232
[9] T-duality: https://en.wikipedia.org/wiki/T-duality
[10] N1 Supersymmetric Dual Quantum Field Model: https://vixra.org/abs/2311.0037
[11] Positronium: https://en.wikipedia.org/wiki/Positronium
[12] Protonium: https://en.wikipedia.org/wiki/Protonium
[13] Cobordism: https://en.wikipedia.org/wiki/Cobordism
A shorter version can be read on thios pdf file: