
A loss of information about the fermionic antisymmetric moment of the atomic system would occur in the Schrodinger complex partial differential equation, causing the misleading notion of two separate kind of nuclear spaces that only can be probabilistically described. The interpolation of partial complex conjugate derivatives would be necessary for a complete description of the evolution of the topological nucleus.
Keywords: Sobolev interpolations, Sobolev inequality, Sobolev embedding, Schrodinger equation, loss of information, linear and non linear partial differential equations, integer and noninteger derivatives, Lorentz force, electromagnetic waves, mirror symmetric bosons, mirror antisymmetric fermions, supersymmetry, dual atomic model, 2×2 complex matrix, complex conjugate operation, actual transposition, -1/2 derivative, +1/2 antiderivative, noninteger spin, topological transformations, function spaces, discrete Fourier, inverse Fourier, Fourier series.
A complex differential equation of second order that doesn’t use all the partial complex conjugate derivatives will loss half of the information of the system – the antisymmetric one – when it comes to describing the evolution of a composite topological system that rotates.
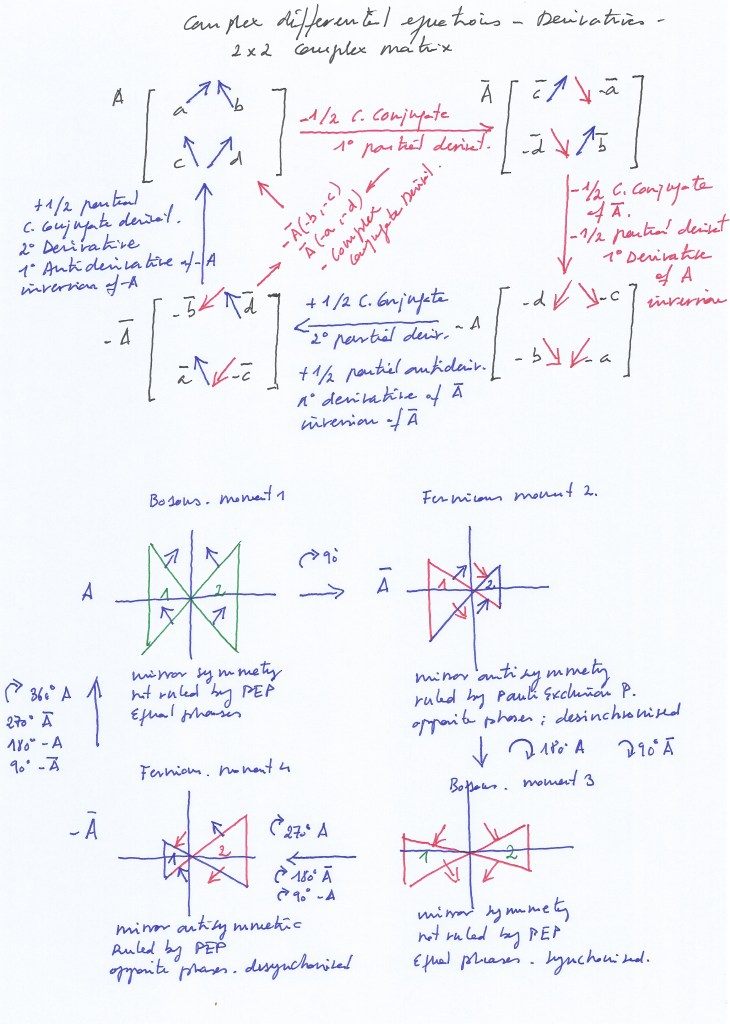
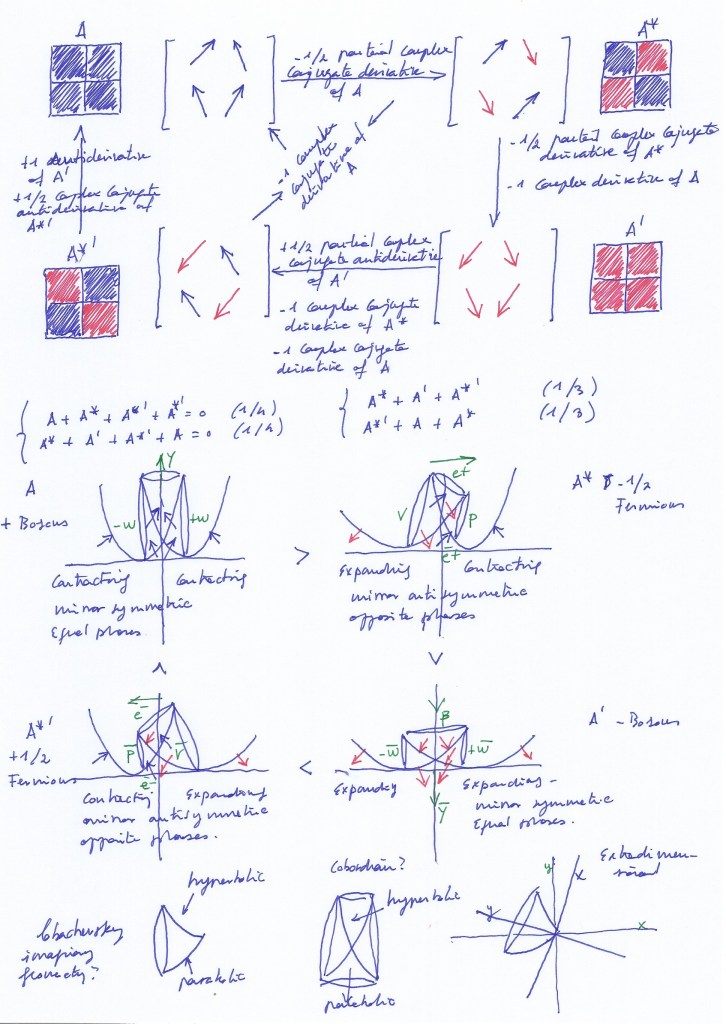
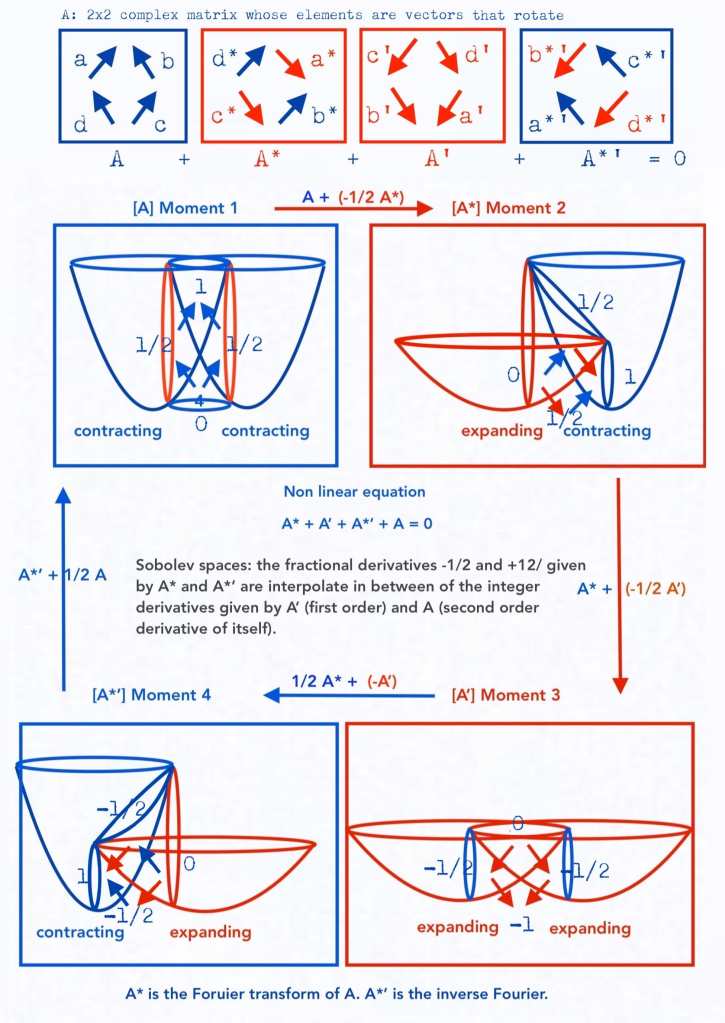
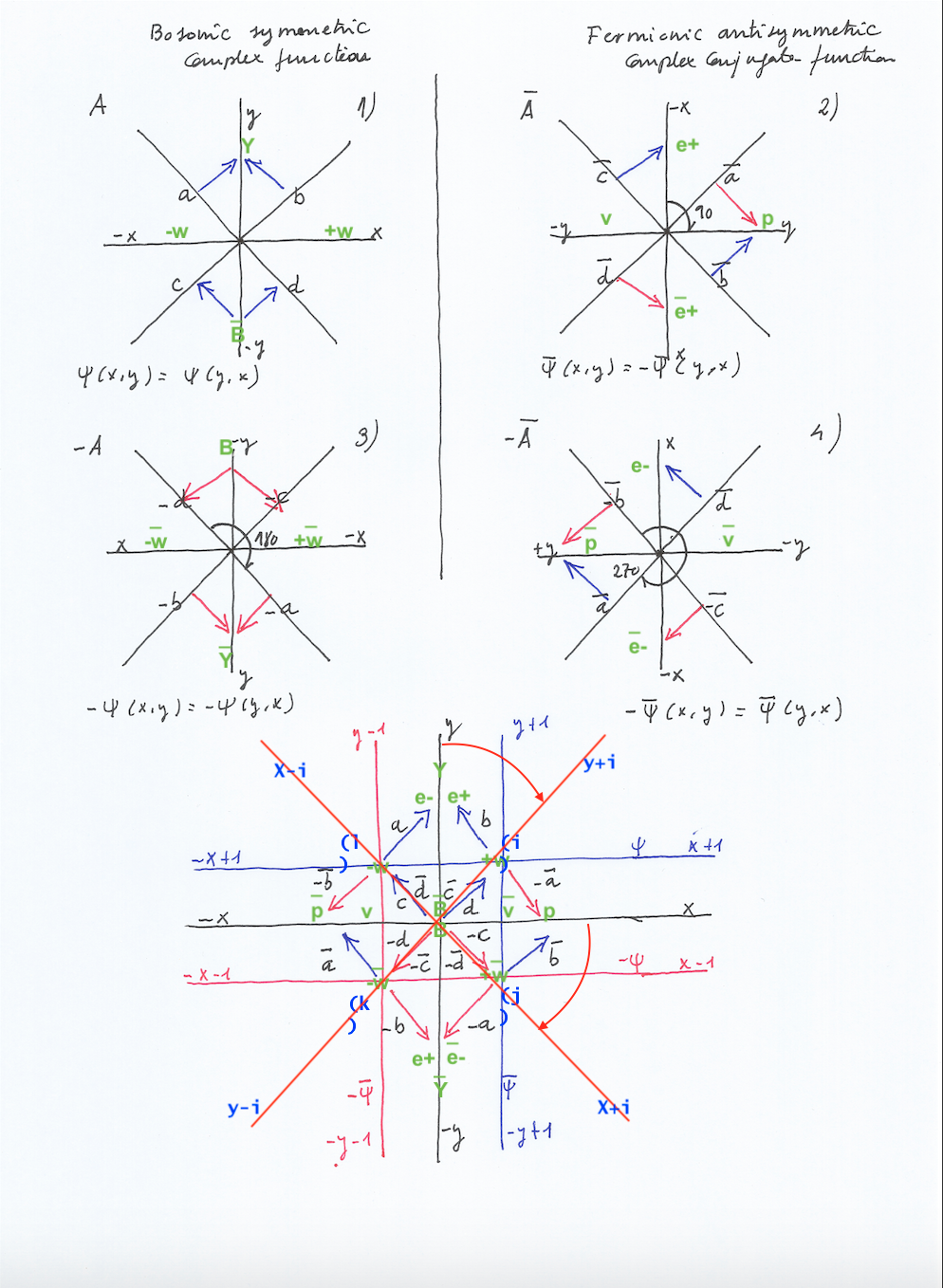
What I meant by «partial complex conjugate derivatives» can be clearly understood in the context of a complex 2×2 matrix whose elements are 4 rotational vectors.
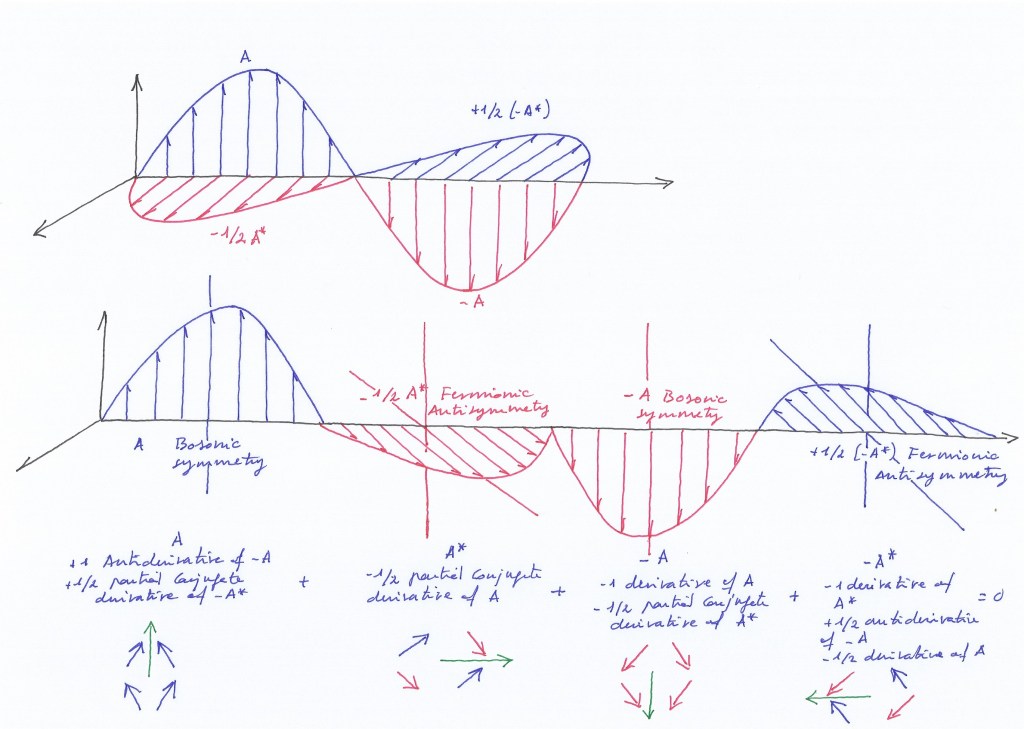
When performing the complex conjugate operation on the initial matrix A, although the 4 vectors rotate, only half of the vectors will change their sign, completing an actual transposition; we can say then that the complex conjugate system A* has -1/2 spin (with respect to the initial state of A where all vectors were positive). This complex conjugation is a -1/2 partial complex conjugate derivative.
A new rotation will change the sign of the two still positive vectors, and so the whole system will have negative spin on the -A matrix. -A is the -1/2 partial complex conjugate derivative of A*, and the integer – derivative of +A.
After a new rotation, two negative vectors will become positive on -A*. -A* will represent the +1/2 partial complex conjugate antiderivative of -A, the +1/2 partial complex conjugate derivative of A, and the integer derivative of A*
A last rotation will change the sign of the two still negative vectors, arriving to the whole positive vectors of A. A is, then, the antiderivative of -A, and the +1/2 partial complex conjugate derivative of -A*.
The Schrodinger equation is a partial complex differential equation of second degree. The ordinary equation describes the mirror symmetric bosons with integer spin; and it also provides an alternative complex conjugate solution that describes the mirror antisymmetric fermions with 1/2 spin.
But, if the atomic nucleus is a complex composite rotational system, the complex conjugate equation is not just an alternative solution, it is an essential part of the evolution of the system; we cannot arrive to the derivative -A without passing through the partial complex derivative A*.
Leaving out of the equation the complex partial conjugate derivatives, the dynamic system only could be described in a statistical way, its evolution will appear to be discontinuous, and we logically think that the system is formed by two separate type of particles that maybe can be super symmetrically linked by some additional that we would be looking for in ever larger particle colliders.
Without intercalating the antisymmetric A* and -A* on the symmetric function of A and -A, the problem of quantum discontinuity arises.
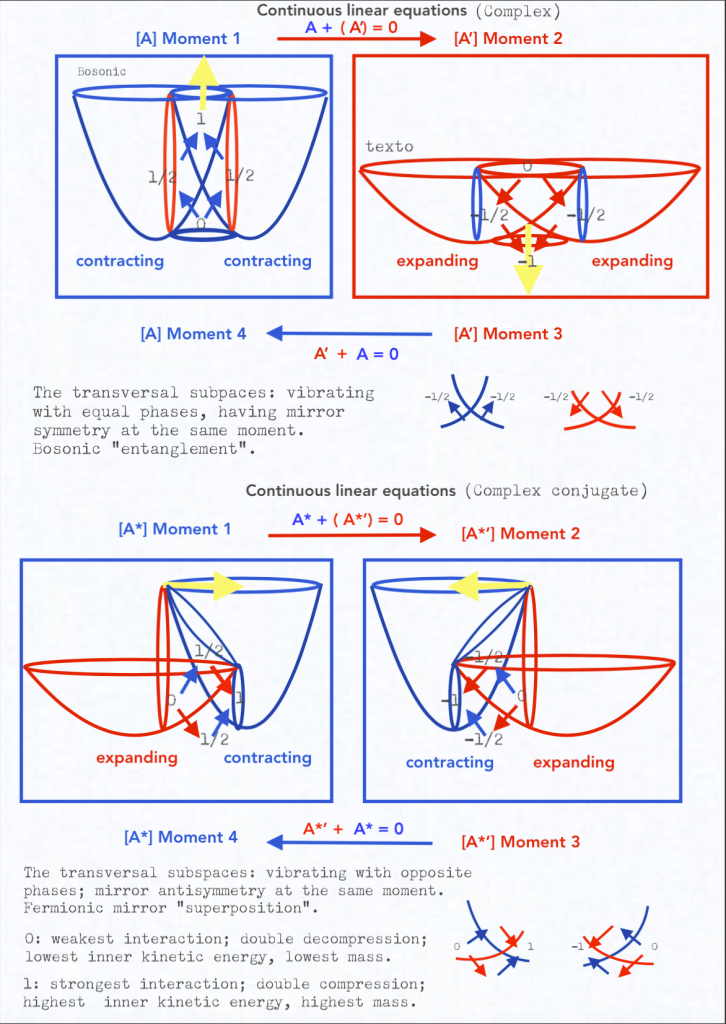
The differential equation should be (-1/2 A*) + (-A) + (+1/2 -A*) + A = 0
The ordinary equation A + (-A) = 0, and the complex conjugate solution A* + (-A*) = 0, lose half of the information and do not allow us to be aware of the topological transformations of the spaces of the system.
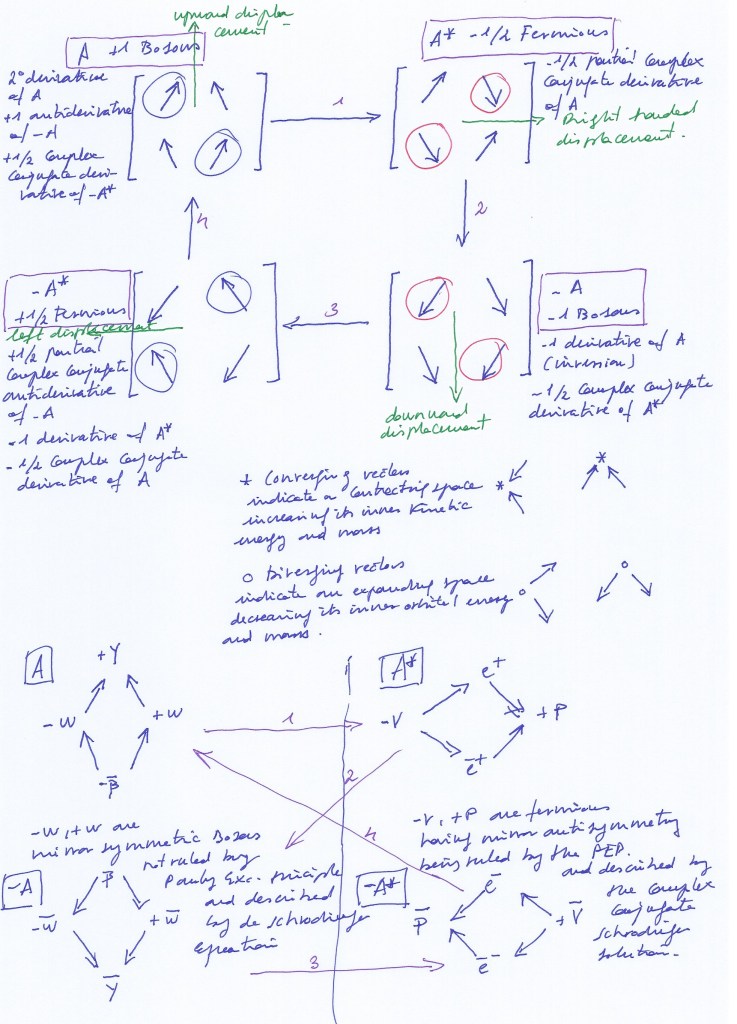
The rotational nucleus could be represented in this way. Two converging vectors indicate a space that contracts (increasing its inner orbital motion and its mass in the higher interaction), and two diverging vectors represent a space that expands (losing its inner kinetic energy and decreasing its mass in the weaker interaction):

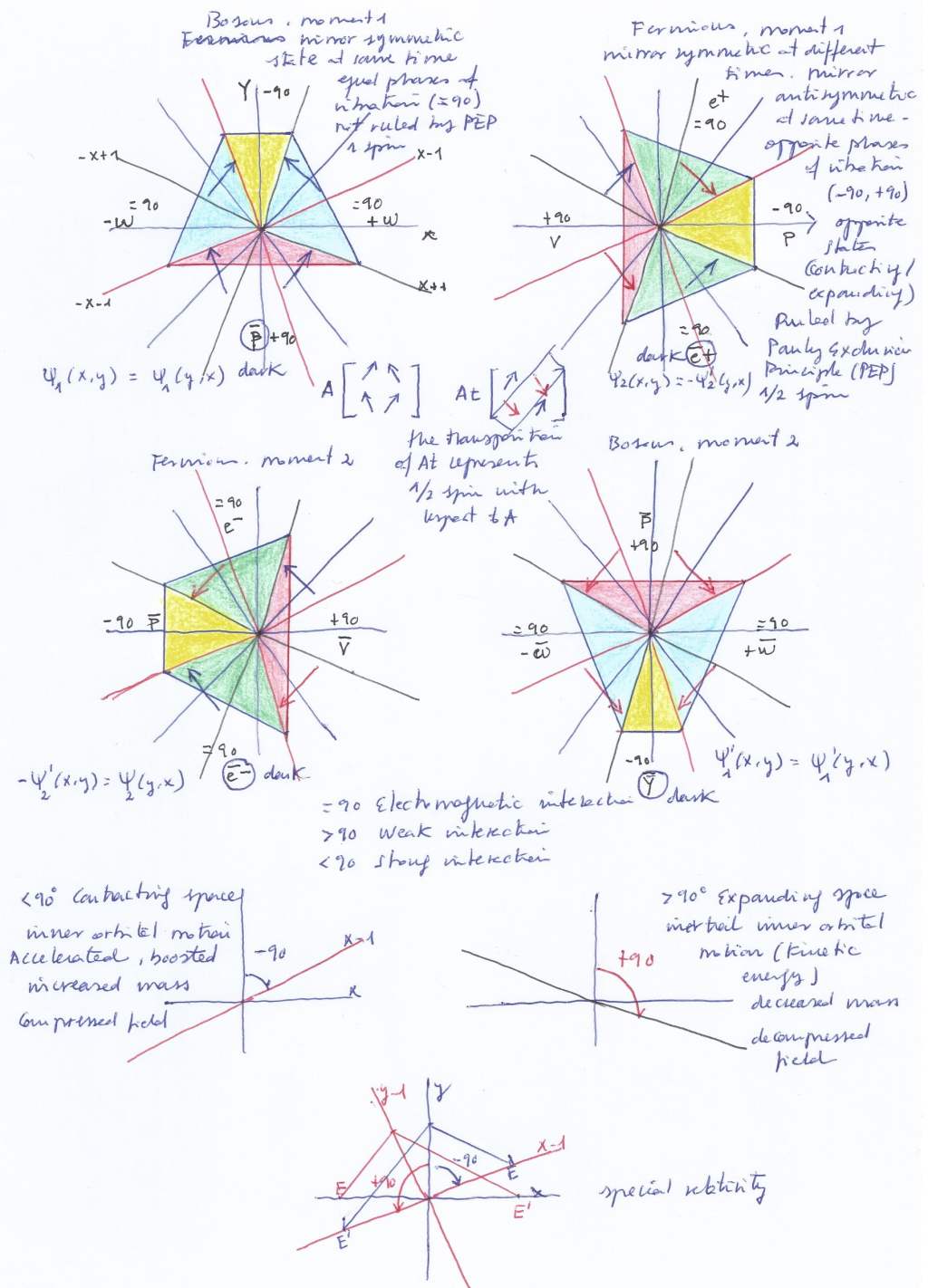
If we simultaneously set on a same space all the moments of the evolution of the system, we would say that it’s perfectly symmetric. Fermions would be placed on the real axes and bosons on the imaginary points. (Although considering the system from the point of view of the rotated coordinates as our spatial reference, bosons would be on our real axis and fermions on the imaginary points).
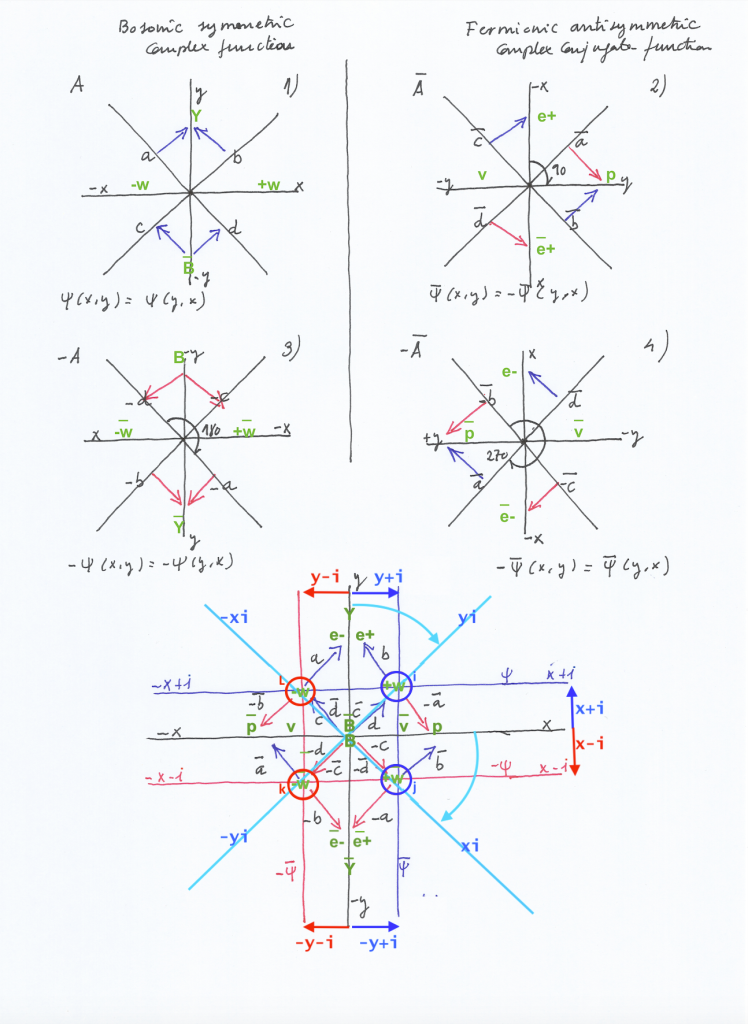
By doing this symbolic representation we can appreciate that it’s necessary to extend our real coordinates XY to the imaginary points X+i, X-i, y+i, Y-i , to make room for the bosonic orthogonal (upward and downward) displacements and the fermionic horizontal (left to right and right to left) displacements, what can be interpret as an expansion or contraction of the complex composite space.
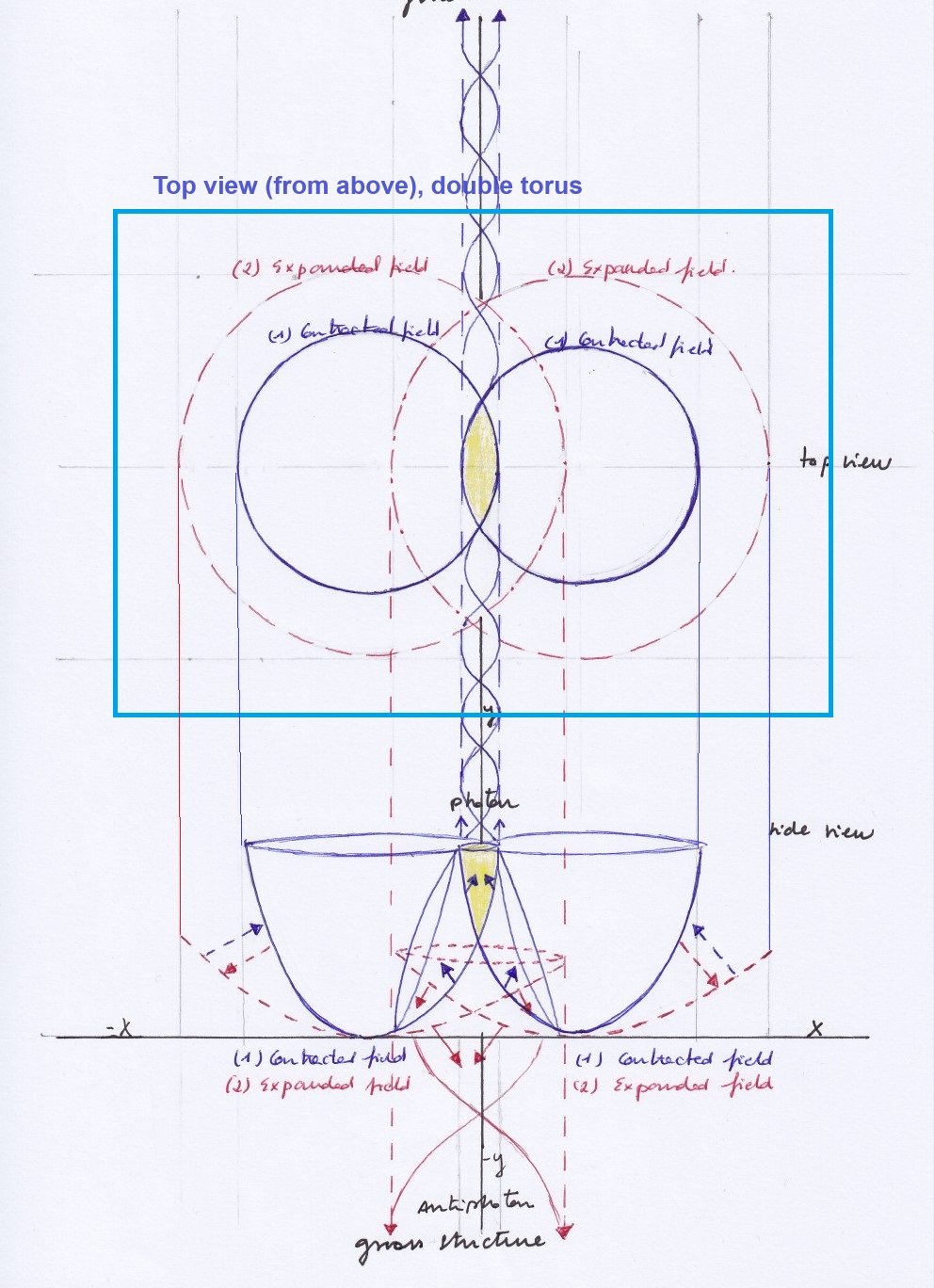
The rotational matrix model would be part of a broader atomic model of two intersecting spaces that vibrate with equal or opposite phases synchronizing and desynchronizing periodically.
The dual atomic system would have a shared nucleus of two orthogonal and two transversal subspaces that will be mirror symmetric or antisymmetric, depending or the equal or opposite phases of vibration:
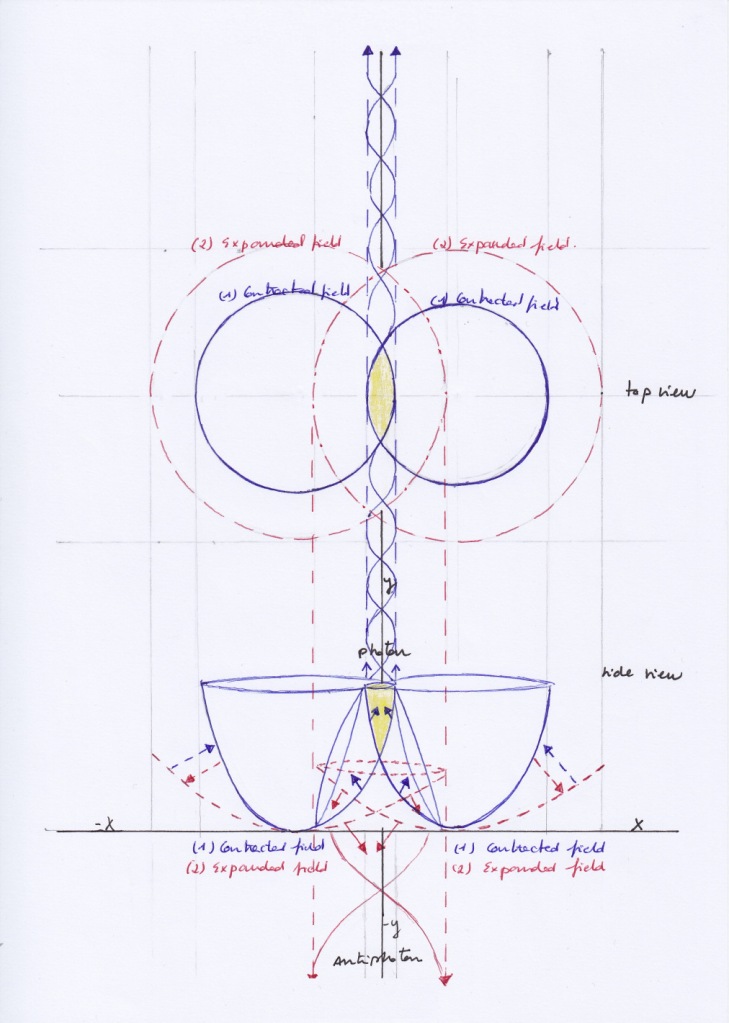

When both intersecting spaces simultaneously contract or expand the transversal subspaces will be mirror symmetric bosons not ruled by the Pauli exclusion principle; when both spaces contract the orthogonal subspace will experience and upward displacement creating an ascending pushing force that will cause a photonic radiation, and when both expand the orthogonal subspace will experience a downward displacement and a decay of its inner kinetic energy.
With opposite phases, when the right intersecting space contracts while the left one expand, the left transversal subspace will expand acting as a neutrino, the right transversal subspace will contract acting as a proton, and the orthogonal subspace will move right acting as a positron; a moment later, when the left intersecting space contracts while the right one expands, the left transversal subspace will contract acting as an antiproton, the right transversal subspace will expand acting as an antineutrino, and the orthogonal subspace will move towards left acting as an electron.
Electron and positron, being the same space moving left or right, will be Majorana antiparticles. Proton and antiproton, or antineutrino and neutrino, will be Dirac antiparticles at different moments. The left and right transversal subspaces, having antisymmetric phases, will be fermions ruled by the Pauly exclusion principle.
In this context, the Pauli exclusion principle is an indication of the symmetry or antisymmetry of the phases of vibration of the mirror subspaces. It must be understood in terms of mirror symmetry or mirror antisymmetry.
Fermionic and bosonic would be then different quantum states (the state of being contracting or expanding and the physical consequences of it in terms of mass, energy and forces) of a sane topological space that evolves through time when its phases of vibration synchronize or desynchronize.
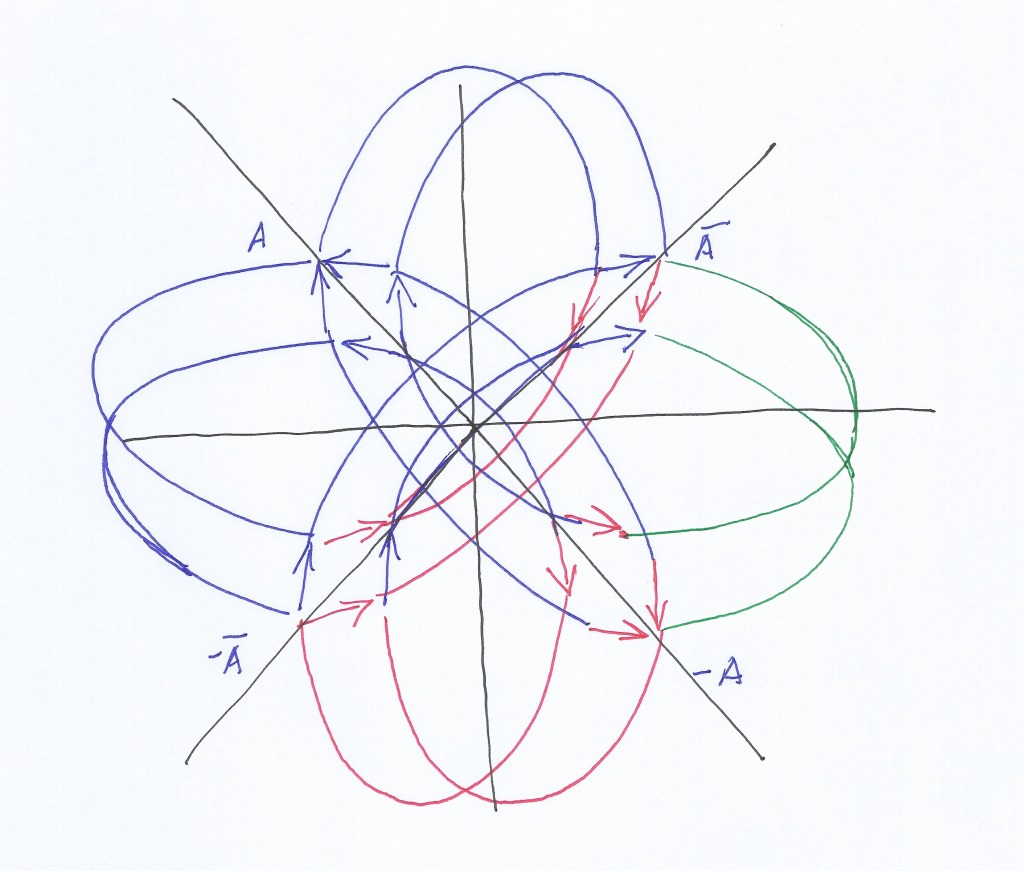
The vector rotational matrix suggests that fermions are the -1/2 or +1/2 partial complex conjugate derivative of the +1 or -1 bosons, and that their topological transformation periodically occurs with the nuclear rotation.
The partial complex conjugate derivatives could also be thought in terms of Fourier transforms: A* would be a discrete Fourier transform, and -A* would be the inverse Fourier. The addition of all the partial complex conjugate derivatives that are A*, -A, -A*, +A, would be the Fourier series.
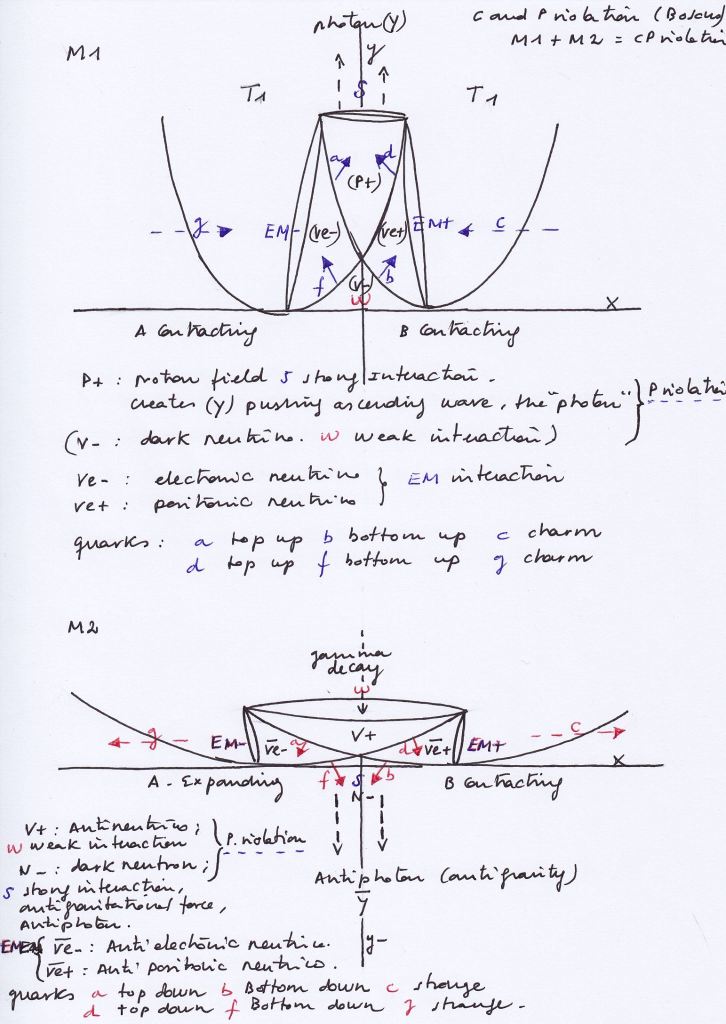
Since the XIX century, electromagnetic waves have been thought caused by the combination of an electric and a magnetic field that vibrate or periodically fluctuate in the orthogonal and the horizontal axes. Here we propose a model of electromagnetic waves created by two intersecting fields that vibrate with same or opposite phases. The orthogonal waves – created by the electrical field in the classical model – will be created when both intersecting fields contract; The horizontal waves – created by the magnetic field in the classical view – will be caused when an intersecting field contracts while the other expands. The positively or negatively charged subspace will move toward the side of the intersecting field that contracts.
It’s known that Heaviside reformulated the Maxwell’s equations using partial derivatives instead of total derivatives and that implied the loss of the description of the Lorentz force. The Lorentz force is the force that the magnetic field causes on a charged particle. In the context of an orthogonal subspace moving left or right, it will not be a force but the geometric consequence of the variation of the curvature of the field that contracts when its intersecting counterpart expands; the charge of the orthogonal subspace will be the pushing force that it will cause when moving left or right towards the contracting «magnetic» space it’s «attracted» to.
The loss of information about the antisymmetric moment of the «magnetic» system represented by the missing Lorentz force that happened with the Maxwell equations when the partial derivatives where used, will be the same loss of information about the fermionic antisymmetric moments that the Schrodinger partial differential equation would be causing in the description of the evolution of the atomic nucleus.
In this sense, the classical graphic of the electromagnetic waves as coexisting fluctuations on the orthogonal and horizontal planes, would be incorrect. The intersecting electromagnetic spaces will simultaneously vibrate with the same or opposite phases, synchronizing and desynchronizing periodically, but their orthogonal and horizontal radiations will be emitted in different moments, the «electrical» symmetric moment (at the orthogonal axis) and the «magnetic» antisymmetric moment (at the horizontal axis), if you will, and they could be expressed in terms of partial conjugate derivates.
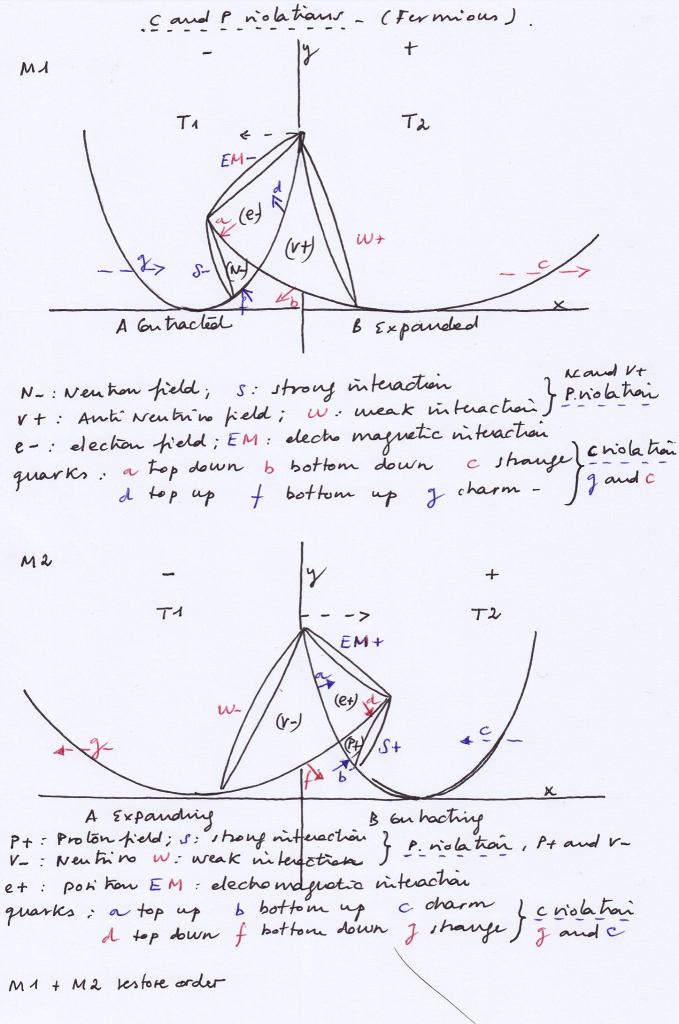
If the electromagnetic iwave rotates, the same apparent discontinuity that was found at the atomic level should also be met here because the radiations of the system would follow the sequence given by the equation -1/2 A* + (-1/2 -A) + 1/2 (-A*) + 1/2 A = 0
(I took the first classical EM wave diagram from Wikipedia The first waves )
The classical representation of the EM waves would imply exactly the same vectorial dynamics mentioned above for the atomic nucleus, although they are shown in a time overlapping way, and that would imply a same topological system of vibrating spaces and nuclear subspaces whose phases synchronize and desynchronize while rotating as the below figure shows.
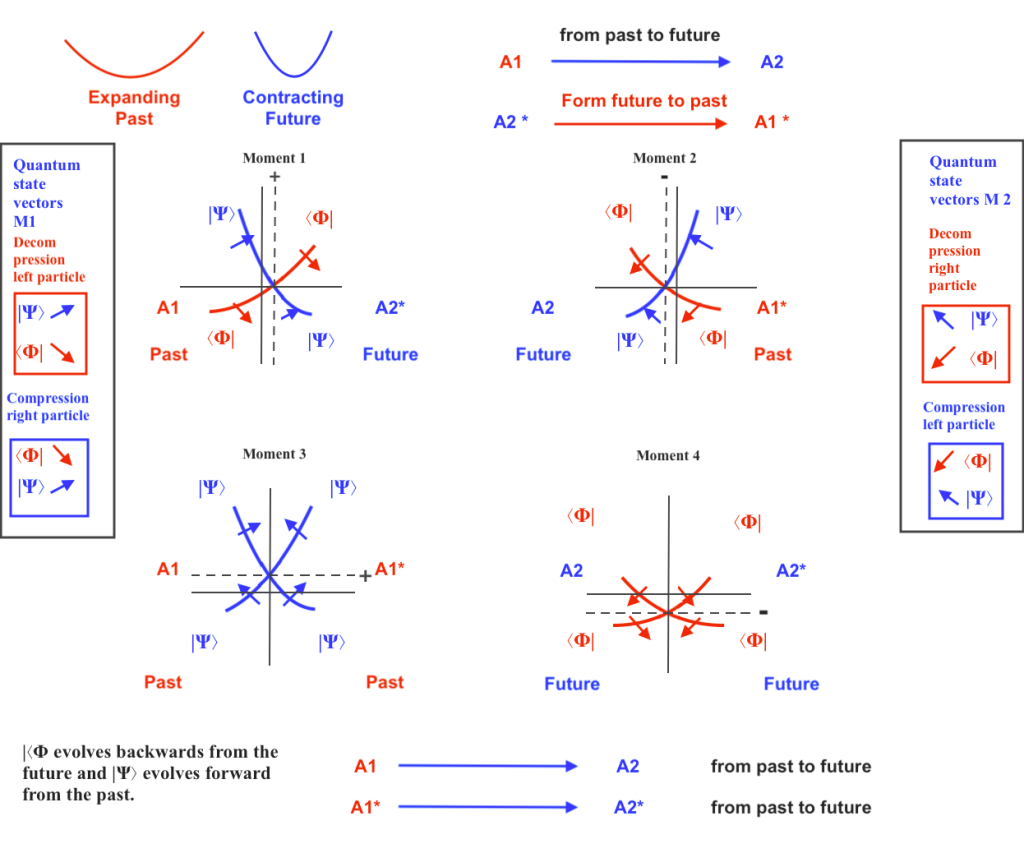
In previous posts I described the model in terms of the Wheeler–Feynman transactional handshake theory, and the two state vector Watanabe model.
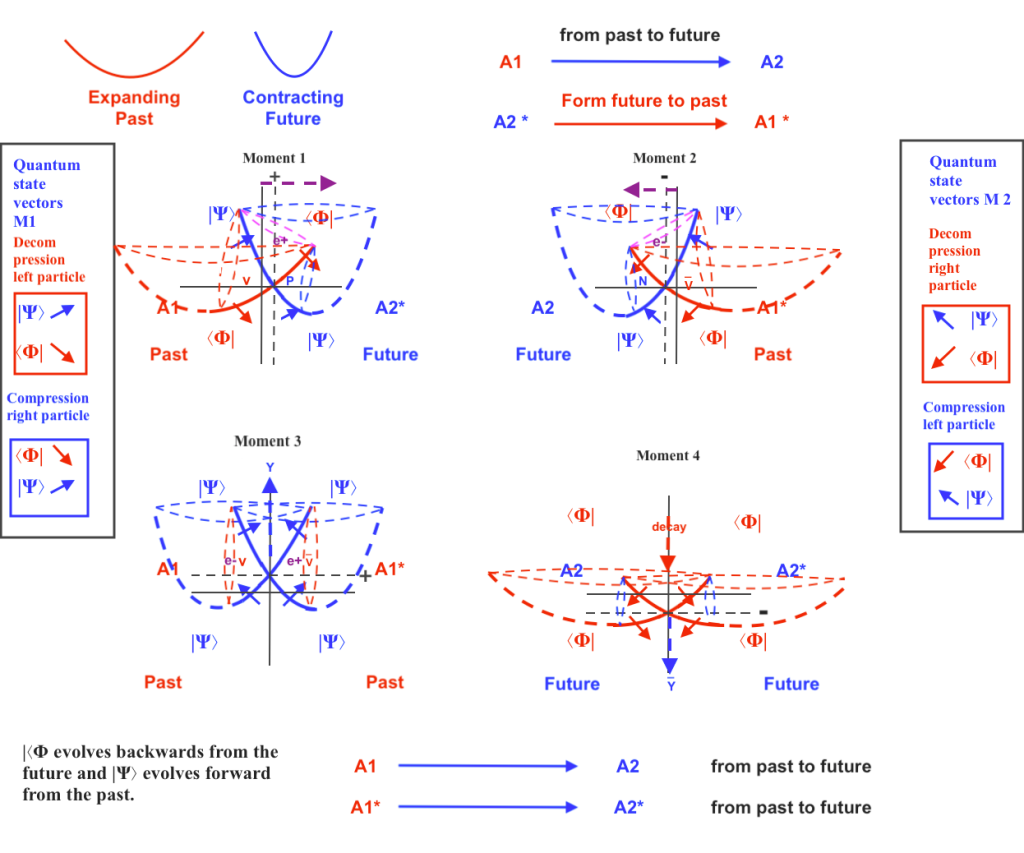
But even more interesting, I think, is the description of the atomic nucleus I made in terms of oxidation -reduction or acid – base reactions, posted some years ago and also recently:
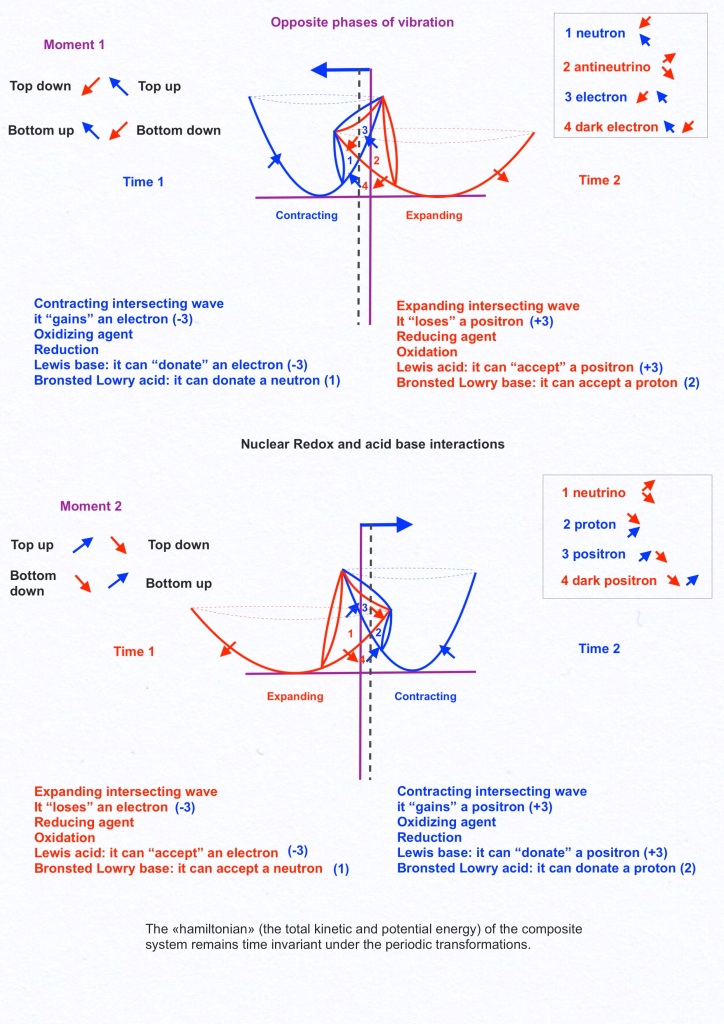
This way of presenting the same ideas in chemistry ways is pretty interesting because I recently found that this same type of approach consisting on two intersecting spaces was already used in the decade of 1950 by Rudolph Marcus in his «Electron transfer theory». Those type of diagrams are called «Marcus parabolas».
«Electron Transfer reactions in chemistry» (R. Marcus)
It seems that this type of approach has been used as well for describing the nuclear transfer reactions , and that for some authors there is some controversy:
«Having been developed by Marcus and many other chemists for more than 50 years, Marcus theory has received extensive application in various fields. Meanwhile, the research object of Marcus theory has been extended from the outer-sphere electron transfer reactions to the inner-sphere electron transfer reactions, even more to the nucleus transfer reactions. Because the reaction coordinates of the transition state of the electron transfer reactions in Marcus inverted region go beyond the region between the initial state and the final state of the reactions in the same reaction coordinate system, which evidently does not obey the natural change logic, we have never accepted Marcus theory as a scientific theory, even though some experimental observations were reported by Miller and Closs as well as many other chemists to support Marcus inverted region.»
Here an interactive demonstration: https://demonstrations.wolfram.com/MarcusTheoryForElectronTransferInPhotosystemII/
Marcus even spoke about the inverted region. This is one of his representations:
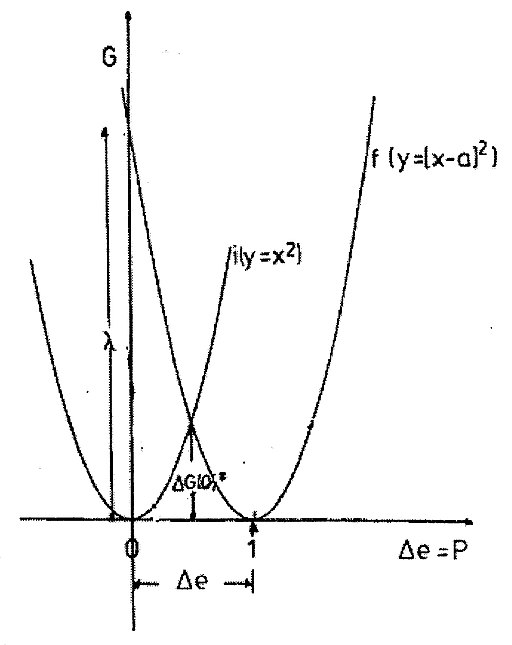
Looking in Google images for the term «Hypersurfaces» that I found at https://www.wolframphysics.org/, you can see the below picture in the next article related to the Marcus theory: «Intermolecular motion of electrons and nuclei: Chemical reactions»
https://www.sciencedirect.com/topics/mathematics/hypersurfaces:
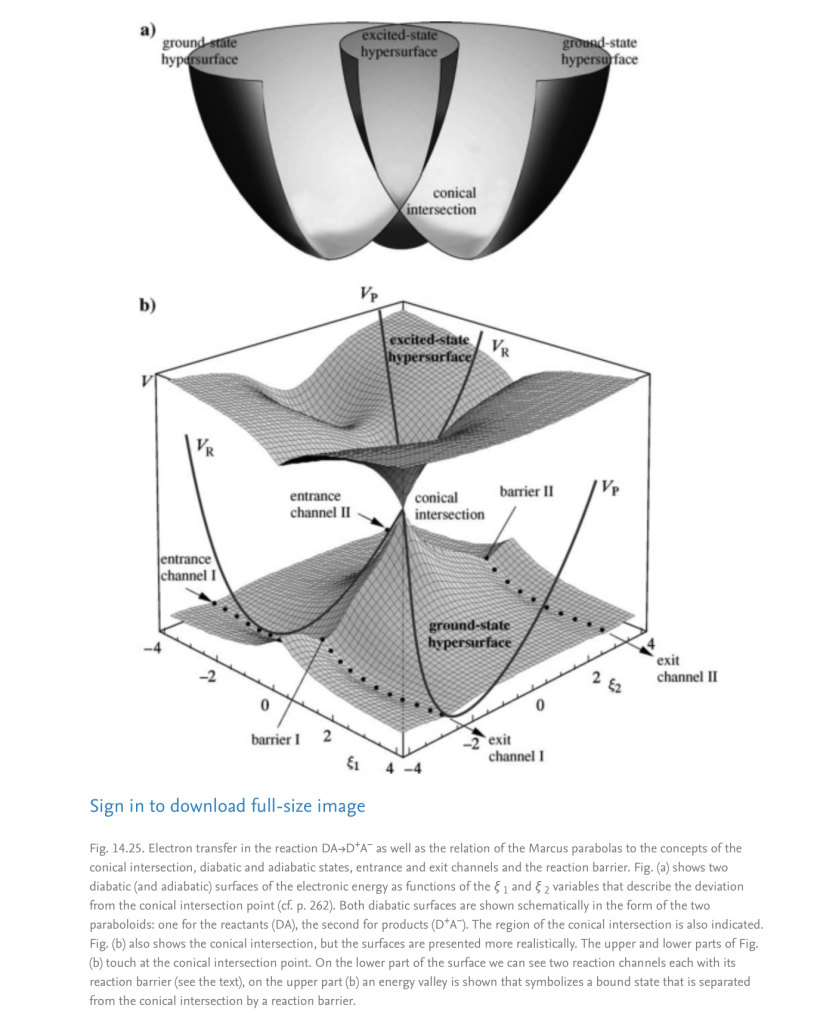
Very familiar, isn’t it?
Maybe the dual atomic model of intersecting spaces could be thought as a generalization of the Marcus theory for the electron, although I think he didn’t consider the moving subspace as the electron/positron space itself, and the inverted region he mentioned as the inverted anti electron/positron. I will research about this new interesting finding.
Finally, it’s also interesting to mention something about the mathematics of the dual atomic system. so call «Function spaces».
It’s known (1) that «in mathematical analysis, an interpolation space is a space which lies in between two other Banach spaces.
The main applications (of the interpolation spaces) are in Sobolev spaces, where spaces of functions that have a noninteger number of derivatives are interpolated from the spaces of functions with integer number of derivatives».
In the context of the 2×2 complex matrix, each permutation can be thought as a derivative of the previous state, causing an exponential increment or decrement. So, starting from A, and performing the complex conjugate operation, as only two vectors change their sign becoming negative in what implies an actual transposition, the operation will imply a –½ partial complex conjugate derivative represented by A*.
Performing a new complex conjugate operation on A*, two new vectors will become negative, and the whole system will have negative vectors on –A. We could also represent –A as A’ to indicate that A’ is the whole derivative of A.
So, what we are representing with the partial complex conjugate derivatives by means of the rotational matrix, seems to be related to the mathematical development known as «Sobolev» spaces. The non-integer number of derivatives would be the case of –½ A* and +½ -A*, while the whole integer derivatives would be the case of –A and A.

To be able to describe the evolution of the nuclear spaces, and avoid the loss of information, the equation that describes them should consider the atomic nucleus as a case of Sobolev spaces, intercalating A* and -A* in between of A and –A.
The subspaces formed by the intersecting spaces, could be considered as function spaces.
In this complex rotational context, where the «weak», fractional, or noninteger derivatives A* and –A*’ must be interpolated in between the «strong», whole, or integer derivatives A, A’ and A’, A to follow the correct continuous and sequential transformational flux, the Sobolev inequality would be given by the antisymmetry between the mirror antisymmetric subspaces described by the function spaces related to the complex conjugate –½ A* and +½ A*’ derivatives.
Sobolev embedding of A* in -A* and vice versa would take place through thought time, being mediated or vehiculated by the topological transformations (the phases synchronization) given in the symmetric -A and A.
Another attempt to show it clearer:
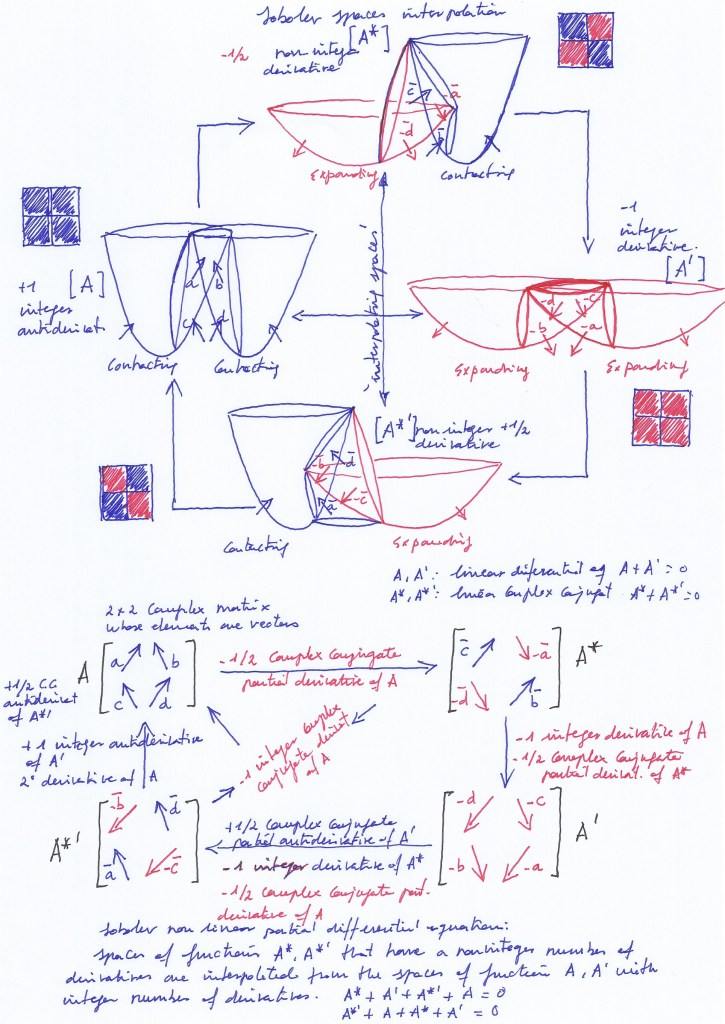
It surely would be more intuitive to put the A and A’ diagrams on the vertical axis and the A* and -A* on the horizontal ones to show that in the case of A,-A there’s an upward and downward displacement of energy and mass through the orthogonal axis, separate by the interpolation of A* and -A*, while in the case of * and A* there’s a left to right and right to left displacement through the horizontal axis, separate by the interpolation of A and -A.
The interpolation would not be only about interpolating the noninteger derivatives A* and -A* in between of the integer derivatives A, -A, and -A, A, but also about interpolating the integer derivatives A, -A in between of the noninteger derivatives A*, -A*, or -A*, A*.
In that sense, the Sobolev inequality would be given by the antisymmetric moment of the topological transformation of the nucleus, when the left and right transversal spaces are mirror antisymmetric subspaces vibrating with an opposite phase at A* and, later, at A*’. So, when it comes to the state of the A* moment, the right transversal space will reach its highest degree of contraction while the left transversal space will reach its highest degree of expansion (and the orthogonal spaces will move towards right). At the A*’ moment, the right transversal space will reach its highest degree of expansion while the left transversal space will reach its highest degree of contraction (and the orthogonal spaces will move towards left).
Sobolev embedding would fix the antisymmetric inequality between A* and A* in the sense that the right-handed contracting transversal space of A* would be embedded in the right-handed expanding transversal space of A*’, and the left-handed transversal contracting space of A*’ would be embedded in the left-handed transversal expanding space of A*.
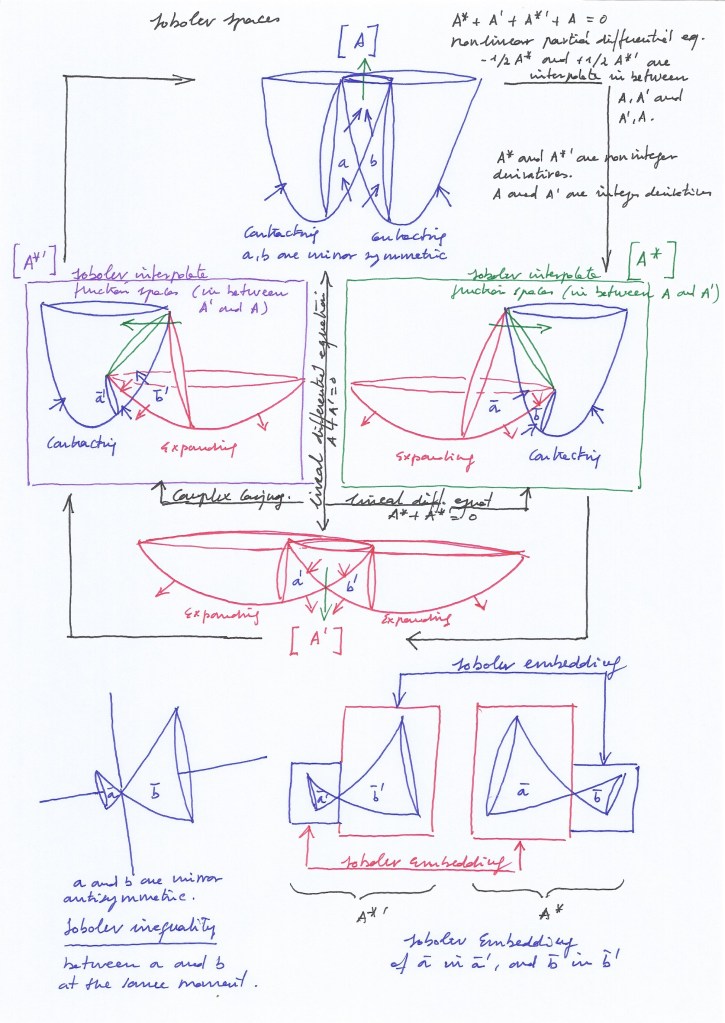
In that sense, the Sobolev embedding would occur through time and it will require the mediation of the topological transformations that occur at A’ and A. By means of that embedding, we get the symmetry of the antisymmetric system through time.
Related to these ideas would also be the notions of «canonical commutation», as «the fundamental relation between canonical conjugate quantities (quantities which are related by definition such that one is the Fourier transform of another), and «conjugate variables».
https://en.wikipedia.org/wiki/Canonical_commutation_relation
https://en.wikipedia.org/wiki/Conjugate_variables
Uncertainty and the necessity of a statistical approach comes because of the use of a linear equation to describe a flux that is non linear as it requieres interpolations.
The Schrodinger equation is a linear differential equation. But there’s a non linear version of it that is applicable «the propagation of light in nonlinear optical fibers and planar waveguides and to Bose- Einstein Condensates.
https://en.wikipedia.org/wiki/Nonlinear_Schr%C3%B6dinger_equation
The interpolate derivatives related to Sobolev spaces here we propose would be part of a non linear partial differential equation. It would be a rotational differential equation.
Einstein field equations about General relativity can be expressed as non linear partial differential equations. Could they describe vibrational composite spaces that rotate? To do it without losing information of the system, they should interpolate the fractional derivatives from the integer derivatives.
– – – – – – –
April 11 update:
But wait, still I have one more thing to share with you.
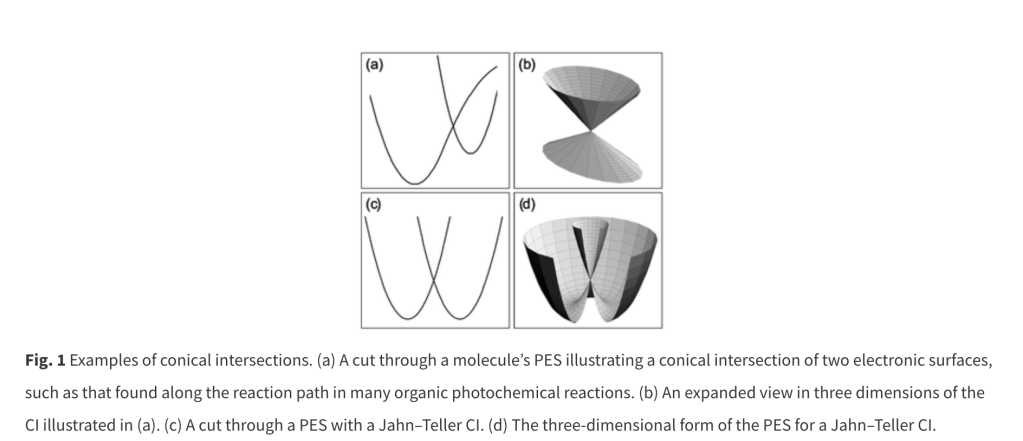
I found that they (physicists and chemistries) are using the term «Conical intersections» to describe this picture that are using when it comes to describing diatomic molecules:
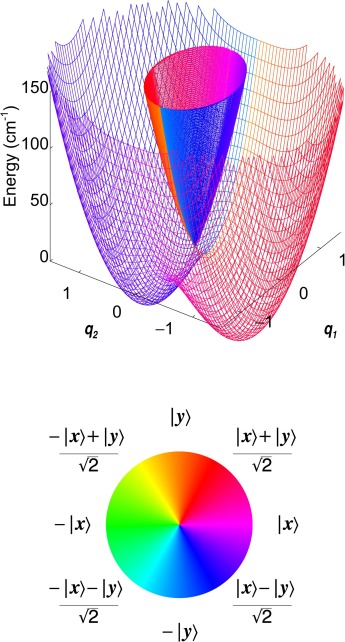
Surprise surprise… very interesting, isn’t it?
It’s surprising to me they use here the geometrical term «cones» or conical instead of physical terms such as vibrating fields, or standing longitudinal waves. i think maybe is to describe the conical shape of the central subspace formed by the intersection of two mirror symmetric spaces, but it doesn’t matter. Our interest now is to know what they understand by «conical intersection» in the context of quantum physics.
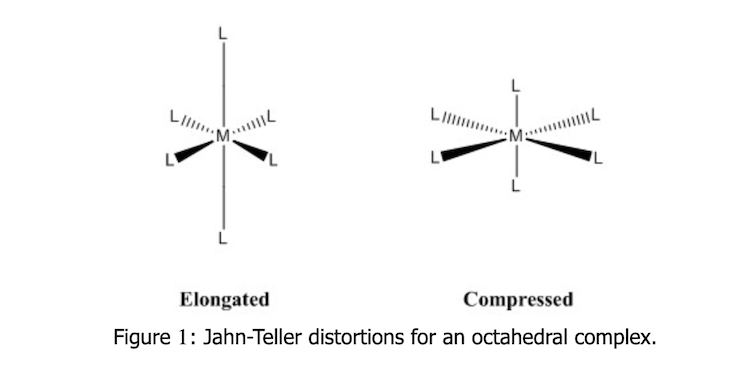
Related to that, we have the so called «Jann-Teller effect or distortion:
In this article they use this same figure, describing them as «examples of conical intersections. (a) A cut through a molecule’s PES illustrating a conical intersection of two electronic surfaces, such as that found along the reaction path in many organic photochemical reactions. (b) An expanded view in three dimensions of the CI illustrated in (a). (c) A cut through a PES with a Jahn–Teller CI. (d) The three-dimensional form of the PES for a Jahn–Teller CI.»
The Jahn – Teller effect describes the geometrical distortion of molecules and ions that is associated with certain electron configuration, a geometric distortion of non linear molecular system that reduces its symmetry and energy.
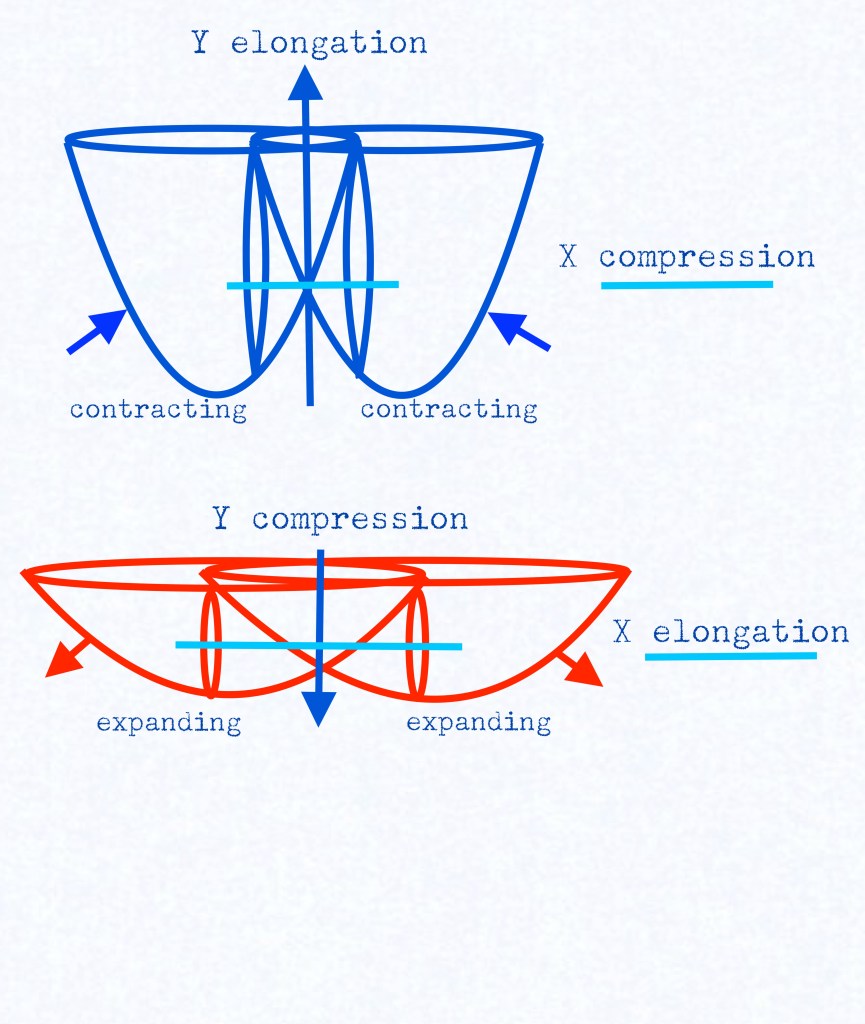
The molecular distortions are related to elongations and contractions:
In the context of our nuclear model that could be expressed in this way, when it comes to equal phases. (speaking about compression and elongation with respect the height and width of the atomic structure, although it could also be expressed in a different way with respect to the shape and physical properties of the nuclear subspaces):
But, as they used this concepts in the context of molecules, we can also suspect that later someone else could have tried to apply the same notion of distorting effect when it comes to the atomic nucleus itself.
And… BINGO! «Transition to deformed shapes as a nuclear Jahn-Teller effect», by Paul-Gerhard Reinhard and Ernst-Wilhelm Otten: https://www.sciencedirect.com/science/article/abs/pii/0375947484904378?via%3Dihub#!
I arrived to these terminologies searching about «geometrical phases»:
«In classical and quantum mechanics, geometric phase is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The phenomenon was independently discovered by T. Kato (1950), S. Pancharatnam (1956), and by H. C. Longuet-Higgins (1958) and later generalized by Sir Michael Berry (1984). It is also known as the Pancharatnam–Berry phase, Pancharatnam phase, or Berry phase. It can be seen in the conical intersection of potential energy surface and in the Aharonov–Bohm effect.
https://en.wikipedia.org/wiki/Geometric_phase
I felt surprised that professor Michael Berry was one of the authors related to the development of the so called «geometric phase» – they speak about the «Berry phase» because I think he should be familiar with the notion of conical intersection, and also about the works that generalize the geometric distortions of the Jahn-Teller effect to the atomic nucleus itself, but it seems is is not, because I wrote him now 2 years ago and he replied me «I cannot comment on your theory because it is too far removed from current ideas and fails to reproduce the quantitative agreement with observations of phenomena that are already understood. Equations and numbers are important.» I felt the temptation of writing hime again with the new developments about the spaces interpolation and how they could be related to the geometric phase and the Jahn Teller distortion when it comes to the atomic nucleus, but I realized it was going to be a waste of time.
I will finally add here some additional pictures to explain the model in the context of a nuclear qubit for nuclear computations (as there’s so much interest now about quantum computers, that are those that without being nuclear, try to emulate quantum behaviour with superposed states in the way described by the standard model of quantum mechanics):
End update.
– – – – – – –
Some more references and some interesting links to research:
interpolation: https://en.wikipedia.org/wiki/Interpolation_space
Function space: https://en.wikipedia.org/wiki/Function_space
Mixing flows: http://personal.psu.edu/axb62/PSPDF/prize1.pdf
Invariant subspace problem: https://en.wikipedia.org/wiki/Invariant_subspace_problem
Bounded operator: https://en.wikipedia.org/wiki/Bounded_operator
Sobolev space: https://en.wikipedia.org/wiki/Sobolev_space
The Spanish version is a bit different: https://es.wikipedia.org/wiki/Espacio_de_Sóbolev
A Sobolev space can be considered as a subspace of a Lp space
Lp spaces (or Lebesgue spaces): https://en.wikipedia.org/wiki/Lp_space
Sobolev inequality: https://en.wikipedia.org/wiki/Sobolev_inequality
Poincare inequality: https://en.wikipedia.org/wiki/Poincaré_inequality
Riemann–Liouville fractional derivatives: https://en.wikipedia.org/wiki/Riemann–Liouville_integral
Fractional calculus: https://en.wikipedia.org/wiki/Fractional_calculus
Einstein field equations: https://en.wikipedia.org/wiki/Einstein_field_equations
Pdf version of the post here
Have a great week


Escribe tu comentario