«De Broglie showed in detail how the motion of a particle, passing through just
one of two holes in screen, could be influenced by waves propagating
through both holes. And so influenced that the particle does not go where
the waves cancel out, but is attracted to where they cooperate. This idea
seems to me so natural and simple, to resolve the wave—particle dilemma in
such a clear and ordinary way, that it is a great mystery to me that it was so
generally ignored». (John Bell, «Six Possible worlds of quantum mechanics»)
When it comes to thinking about nature and building models to understand and describe it, the main question that should be clarified, I think, should be what is the conception of space we consciously or unconsciously have assumed and internalised. What is our initial prejudice about space.
All physics from Aristotle have been built upon the notion of a unique, independent, and static space orbited around its unique center. It’s a kind of monistic conception of space based on the idea that there is a unique universe with a unique center governed by the rules of the unique and eternally inmutable God. Even once Riemann unveiled his influential conception of spatial manifolds, that are composite intersecting spaces formed by subspaces, we still continue thinking about nature in terms of separate fields that as much overlap.
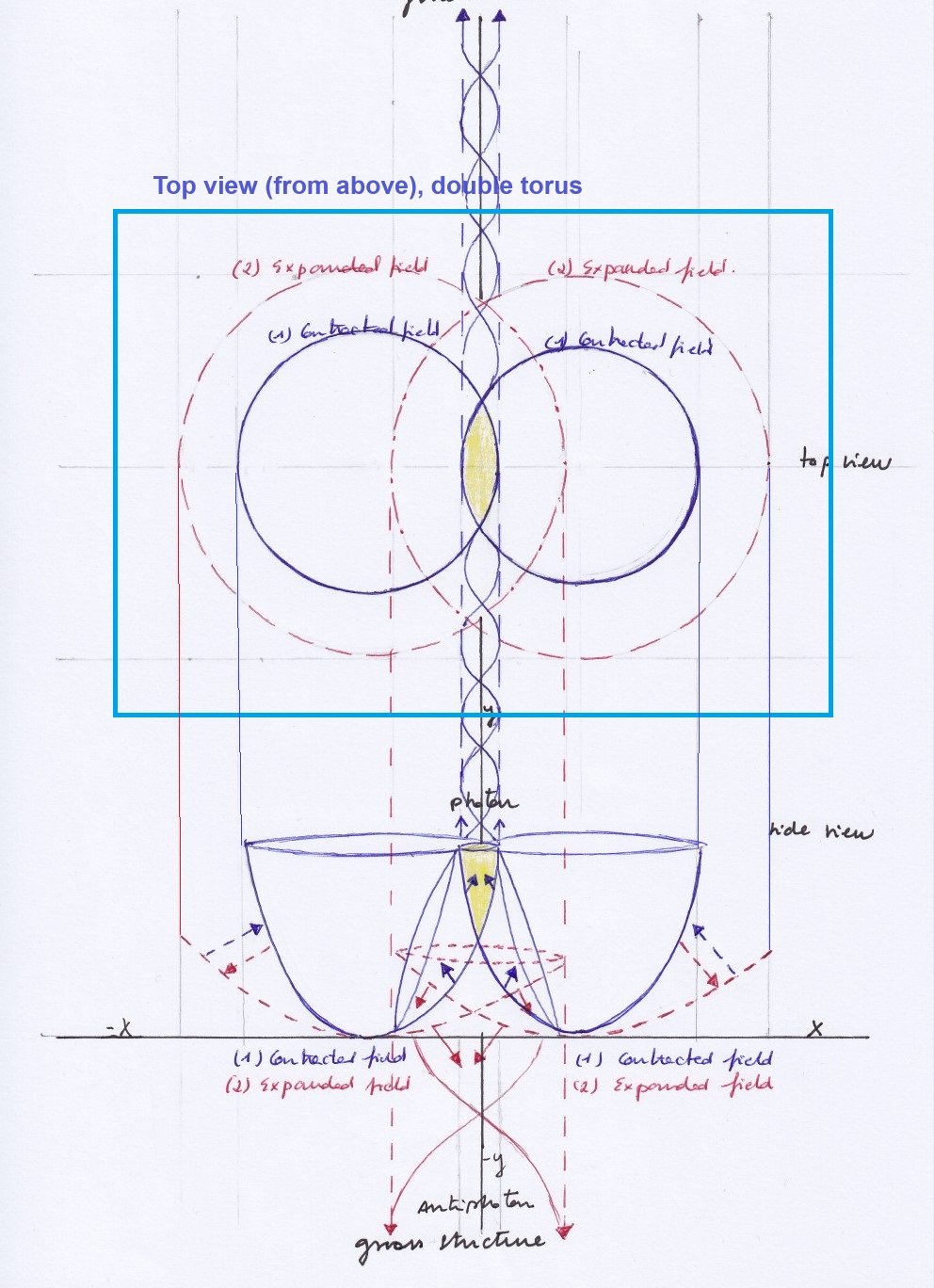
But what would happen if instead of a unique space, the electromagnetic life started only when at least two fields that vary periodically with the same or opposite phase intersect or get partially merged?
By «field» here I think about a longitudinal wave (or a vibrating vortex or concave field) that expands and contracts periodically while vibrating.
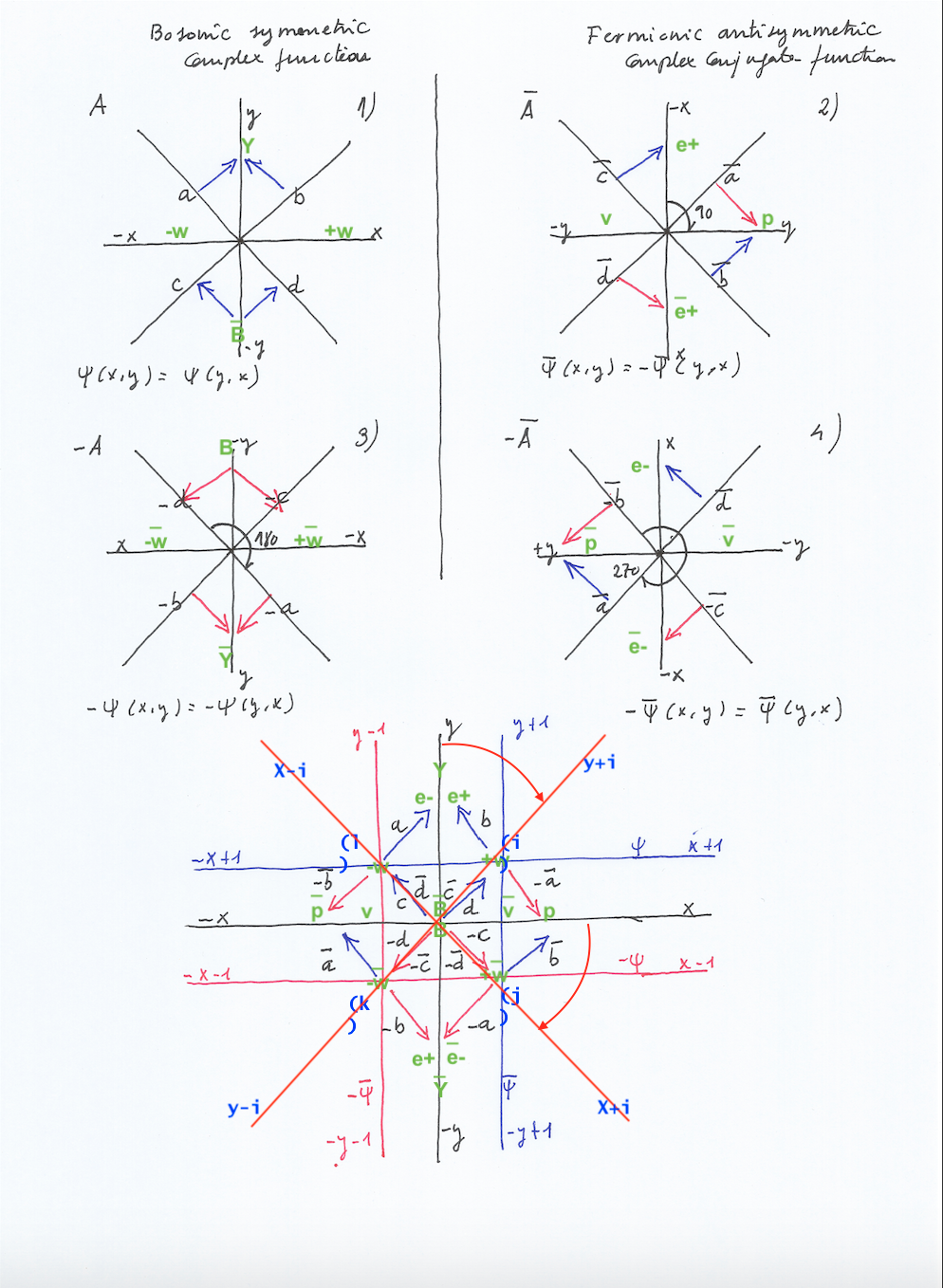
In the concave side of the intersection of those two longitudinal waves it will exist four subfields that will behave in a very different way, having different spacial and material properties, depending on if the phases of vibration of the intersecting fields are opposite or equal:
A. When those phases of vibration are opposite, one of the shared subfields will move in a pendular way left or right towards the side of the intersecting field that contracts (while the other intersecting field expands). The subfield moving towards left is the same subfield that later will move towards right and vice versa, and so that subfield represents its own antimatter.
(A field is the antimatter of another when they both are identical but are placed in opposite places, having mirror symmetry; When instead of two fields there’s only one filed that is its own antimatter, it’s called a Majorana antimatter because of the Italian physicist Ettore Majorana who predicted its oscillatory existence.)
B. When those phases of vibration synchronise becoming equal, that shared subfield won’t oscillate from left to right but it will periodically move upwards and downwards through the orthogonal axis. Moving upwards, the mentioned subfield will contract experiencing an acceleration of its inner orbital motion; and moving downwards it will expand experiencing a decay of its inner orbital motion (or inner kinetic energy).
I think so far these ideas are clear and indisputable, aren’t they?
But I think the intersection of the fields also reveals the existence of other transversal subfields in the concave side of such intersection:
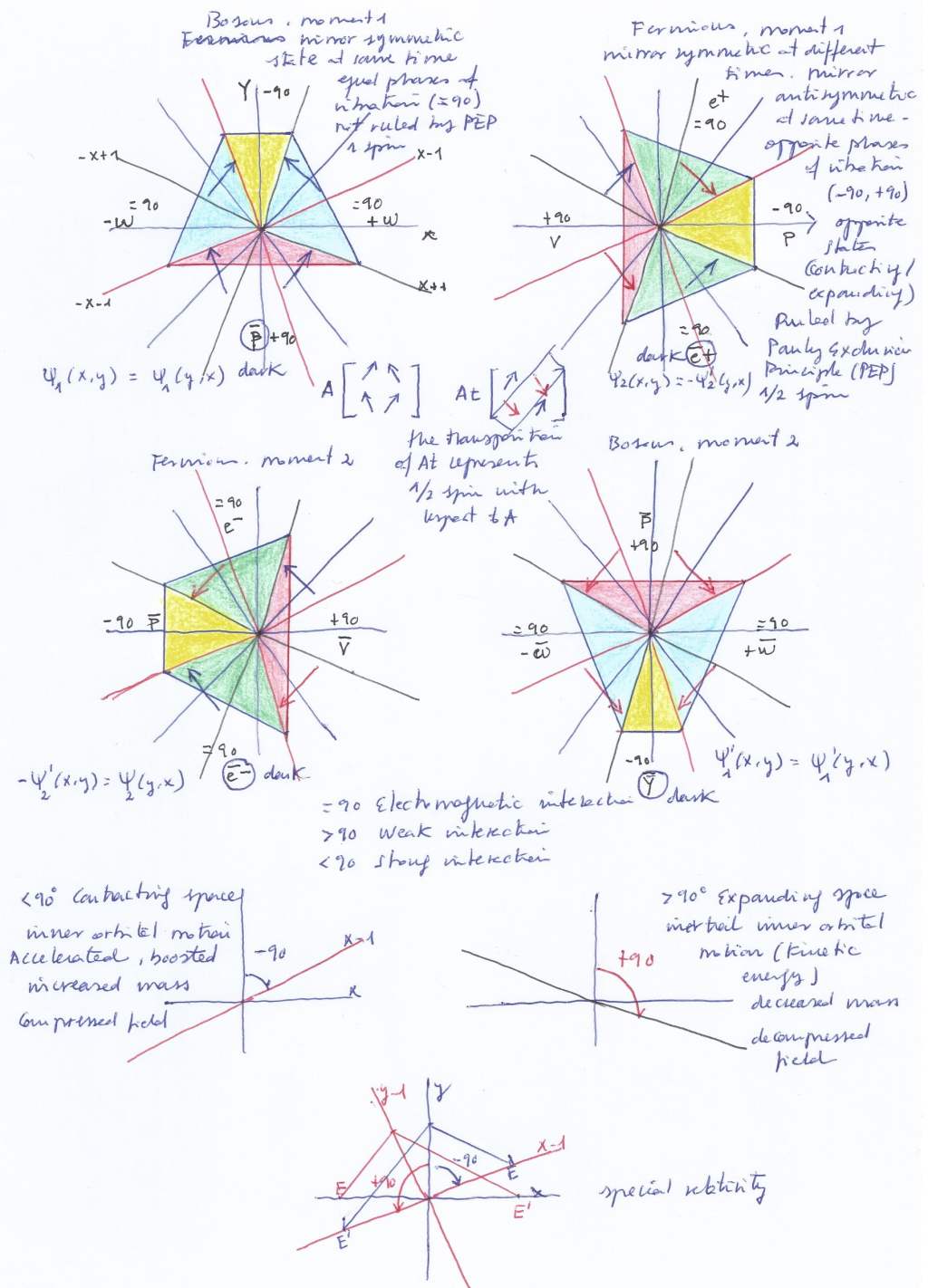
A. With opposite phases, when the left intersecting field contracts and the right handed one expands, at the left side of the center of symmetry there will be a transversal contracted subfield while at the right handed side there will be a transversal expanded subfield. When the left intersecting field expands and the right handed one contracts, the previously contracted left subfield will expand (becoming, in different consecutive moments, the mirror symmetric Dirac antiparticle of the right handed subfield when it was previously expanded), and the previously expanded right subfield will contract (becoming, in different consecutive moments, the mirror symmetric Dirac antiparticle of the left subfield when it was previously contracted).
It can be said the contracted or expanded left and right transversal subfields are ruled by the Pauli Exclusion principle because at the same moment they are not identical, they have a different quantum – expanded or contracted – state (as when one subfield is expanded the other one is contracted and vice versa). They only are identical and distinguishable because of their chiral symmetry at different moments. Then, it also could be said those subfields will be acting as Fermions, and so they must be satisfying the Fermi Dirac statistics.
I understand you can question already this because I kind of reinterpreted the Pauli exclusion principle and I didn’t verify if those statistics work here or do not work. I only conceptually deduced it.
B. With equal phases, when both intersecting fields contract at the same moment, the left and right transversal subfields will simultaneously expand; and later, when the intersecting fields expand at the same moment, the left and right transversal subfields will simultaneously contract. Now, the left and right transversal expanded or contracted subfields will be identical and distinguishable at the same moment, having mirror chiral symmetry. As they are identical but chiral antimatters existing with mirror symmetry at the same moment and having the same – expanded or contracted quantum state – they are not being ruled by the Pauli Exclusion principle, and so they must be satisfying the Bose Einstein statistics being bosons.
According to the Pauli exclusion principle, fermions and bosons have different spins, fermions 1/2 spin and bosons 1 spin. But what does it physically mean? I think the actual meaning of the 1/2 and 1 spin could be the following:
When it comes to fermions we are dividing 1 orthogonal subfield / 2 intersecting fields, or 1 contracted transversal subfield / 2 intersecting fields, or 1 expanded transversal subfield / 2 intersecting subfields = 1/2
When it comes to bosons, we are dividing 2 contracted transversal subfields / 2 intersecting fields, or 2 expanded transversal subfields / 2 intersecting fields = 1.
In this case we are only considering the quantum state of the subfields, but I think this could be refined if we considered also the quantum state (expanded or contracted) of the two intersecting fields that form those subfields.
But what all these subfields would represent when it comes to atoms? I think the electromagnetic atom should be interpreted as a dual system of two intersecting longitudinal waves, having a shared atomic nucleus formed by those two intersecting or partially merged waves. The above mentioned subfields would be then the subatomic particles of central nucleus shared by the dual electromagnetic atomic system.
(I think a single atom could be thought yet as a unique vibrating longitudinal wave that emits radiation, but in that case it did not have an electromagnetic subatomic nucleus. An isolated vibrating field would not have electromagnetic properties until getting intersected to another vibrating field.
In a dual atomic system, the same subatomic subfields will act as fermions or bosons depending on the phases of variation of the intersecting fields, evolving from fermions to bosons and vice versa, periodically through time, when synchronising and desynchronising the phases of vibration of the intersecting fields.
In this sense it could be thought that when it comes to fermions there are two time dimensions (one for the different phase of variation of each intersecting field) that will converge in a same time dimension when it comes to bosons, and will diverge again in two time dimensions when they evolve to fermions again, and so on.
This is a supersymmetric topological system that keeps the covariant symmetry through time by means of the rotational permutations of the quarks. I call quarks here as the forces of pressure caused by the displacement of the two intersecting fields when contracting or expanding; but quarks in this model are actually the force of pressure caused by the inner or outer side of those intersecting fields when varying. I represented them with vectors in the below diagrams.
How each subfield will correspond to the currently known subatomic particles of the atomic nucleus?
A. Opposite phases of variation, fermions:
Moment 1: The moving right to left subfield will be an electron, the contracted left subfield will be a neutron, and the expanded right subfield will be an anti-neutrino:
Moment 2: the moving left to right subfield will be a positron, the expanded left subfield will be a neutrino, and the expanded right subfield will be a proton.
The proton would be then the antiparticle of the neutron (as Heisenberg already suggested), but at different moments, and it will decay at the next moment in an antineutrino whose expanding pushing force will create the «quark» of the electron. Electrons and positrons in this model also are «created» by quarks.
It’s currently accepted that the neutron is not the antimatter of the proton because they have slightly different masses. But it’s also known that the proton’s decay is not being clearly explained by the currently accepted atomic model as its decay has not being experimentally observed yet by using the predictions and calculations provided by that model.
B. Equal phases of variation, bosons:
The subfield ascending through the orthogonal axis will create a photon with an inner double helix spin, and it will decay a moment later. When the decay happens at the concave side of the dual system, at its convex side it will appear an inverted pushing force that will be an antiphoton, correspondent to the decay of the descending subfield. Photon and antiphoton will be ruled by the Pauli exclusion principle because they cannot exist at the same moment at both, the concave and convex, sides of the system, and so, being in the bosonic dual atom it would imply a violation of the Pauli Exclusion principle.
I’m not sure about the term to identify the two transversal expanded or contracted subfields, but as they have a pushing quark like the electron has and they have a similar volume than the neutrino, they maybe could be considered as two electronic neutrinos when they are expanded; it would be rest to name them when they both are contracted.
An interesting observation is that with equal bosonic phases, the two transversal subfields follow a phase that is opposite to the phase of the vibration of the intersecting fields; so, when the two intersecting fields contract at the same moment, both left and right transversal subfields will be expanded, and later, when the two intersecting fields expand at the same moment, both left and right transversal subfields will be contracted.
It does not happen when it comes to opposite fermionic phases: when the left intersecting field contracts and the right one expands, the left transversal subfield will contract and the right one will expand; and when the left intersecting field expands and the right one contracts, the left transversal subfield will expand and the right one will contract.
Let’s go to represent now the vectors that act as quarks in the dual model:
And let’s visually see now how they are supersymmetric. The existence of supersymmetric particles that would link the two separate (by the quantum mechanics and Quantum field theory models) kinds of matter, fermions and photons, where predicted by the string theories. But those particles that would be symmetric through time (that is why they are called super symmetric) have not been found yet for the biggest energy collider of particles, the Large Hadron Collider or LHC. That fact of the missing supersymmetric particles disappointed many string theorists.
In this model the supersymmetric particles are quarks, and they have already been detected, no new particle is necessary. But the main problem of quantum theories is that they are probabilistic, and they do not have a visual representation of the topology of the atomic nucleus. For current physicists, the atom and the subatomic particles are like a foggy cloud where they can do their probabilistic and statistical calculations.
In this same sense, the Schrodinger’s equation describes how the atomic wave function evolves, but in a probabilistic way; what actual topology does represent that wave function? Is it about a single vibrating field? Is it about inner subfields inside of such a vibrating field? or is it about two partially merged vibrating fields and their inner subfields?
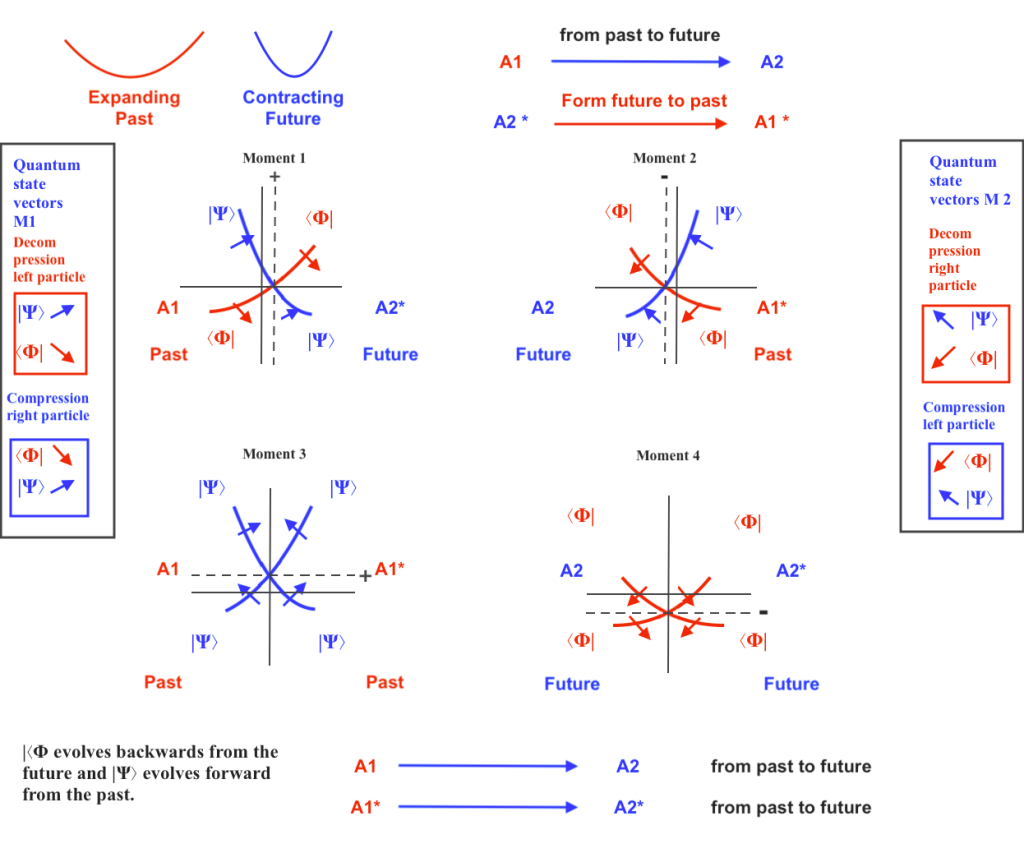
If the wave function represents how a dual vibrating system and its vibrating subfields evolve, I think it is natural to think that wave function will periodically – not randomly – collapse because the subfields of the system are going to have different behaviours depending on the moment the phases of vibration are. In this sense, I think the dual atomic model would be compatible with the spontaneous collapse theories of the wave function(here I think they speak about spontaneous collapse that is not caused by the measure made by an observer).
The dual atomic model would not be conceptually incompatible either with the wave pilot theory that was already proposed by De Broglie and Bohm, but instead of thinking about a single wave pilot we here consider two intersecting pilot waves that form their shared atomic nucleus. What drives the subfields in different horizontal or vertical direction and the ways they evolve changing through time, must be two intersecting pilot waves which the subfields are a local part from. (In the dual intersecting pilote wave would not be necessary to use probabilistic calculations).
In this same sense, the spontaneous collapse of the wave function and the dual waves pilot concepts would not be incompatible with the idea of the existence of many worlds or parallel universes, if we think in a model of a dual atom where the multiverses (or pilot waves universes) are not parallel but intersected, and the many worlds are many sub-worlds inside of the intersecting system that forms them.
(The spontaneous collapse theories of Ghirardi, Rimini, and Weber, the De Broglie and Bohm wave-pilot, and the many worlds interpretation of Everett, are three of the main theories or interpretations that do not follow the merely instrumental approach of the Copenhagen interpretation of quantum mechanics).
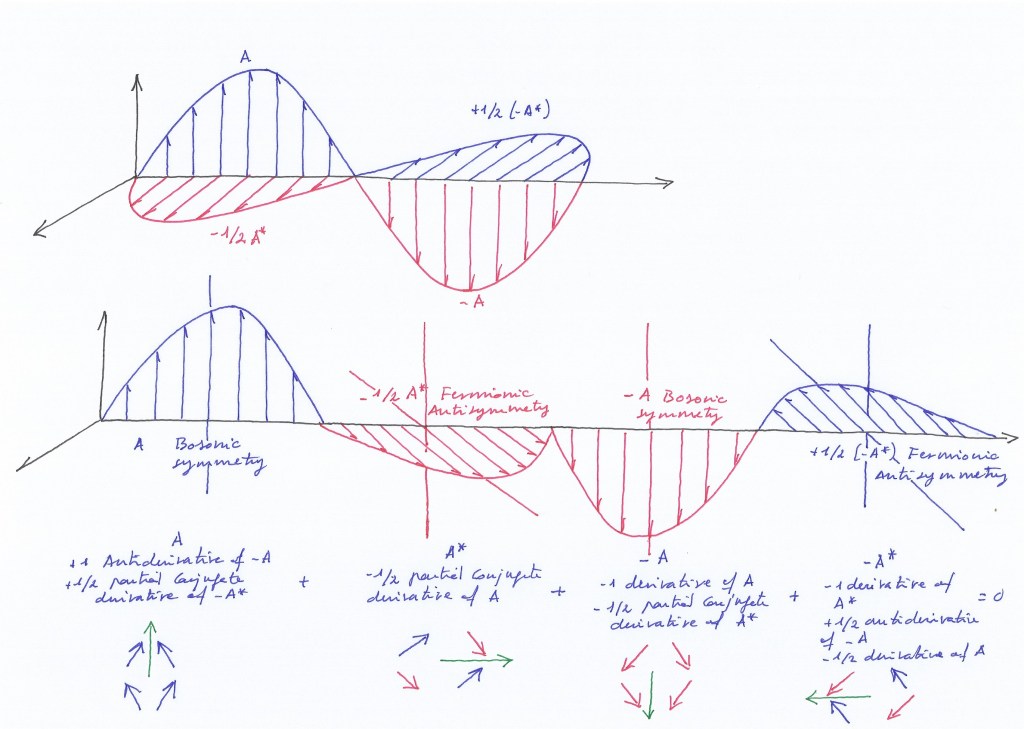
On the other hand. If we think about a vibrating field as a cat, and imagine it’s dead when the field is expanded and alive when it’s contracted, we only can rationally say the cat is going to be dead and alive at the same moment if we have two identical cats that are distinguishable because they both are mirror symmetric cats, having a chiral symmetry (or opposite inner orbital spins when it comes to vibrating fields); It can be imagined that instead of two, we have only one cat an a mirror that reflects its image.
If at the same moment, the left side of the mirror the cat-subfield is alive-contracted and at the right side of the mirror the cat-subfield is dead-contracted that Schrodinger cat will be a fermionic cat.
(We can think about a virtual particle as a subfield that now does not actually exist at the right side of the dual system because just at this moment it exists at the left side; it’s called virtual because although it currently does not actually exist at the right side it «potentially» exists there now, it has the potency of being existent there a moment later, as the existing left subfield is going to be displaced towards the right side. We can think as an alive cat the actual subfield and a dead cat its virtual – yet actually not existing – mirror symmetric subfield if you want to keep playing with your imagination. But I think virtual particles where simply thought about by physicists as another tool for making the equations about the symmetry of their atomic system mathematically consistent.)
But when the time comes and our perplexed Schrodinger physicists open the box, surprise surprise, the dead and alive cat will have become a dog that will be dead (or alive) at the same moment on both sides of the mirror. It will be a bosonic dog. If our physicist thinks that’s a kind of magician box, that will be only because he will not know the whole topology of that space time evolving system.
I think superposition and entanglement are not currently being correctly interpreted. Superposition to me is about two identical quantum particles with their quantum – expande or contracted – states that exist at the same moment but that are distinguishable because they have an opposite sign, they have a mirror spatial symmetry.
Representing as 0 a contracted field or subfield and 1 an expanded field or subfield, 1 a field that moves left or right, 1 a subfield that moves upwards and 0 a subfield that moved downward, we have this next result: (the 1s and 0s inside of the parallel bars represent the state, contracted of expanded, of the pilote waves that are arranged by pairs because they will be intersected).
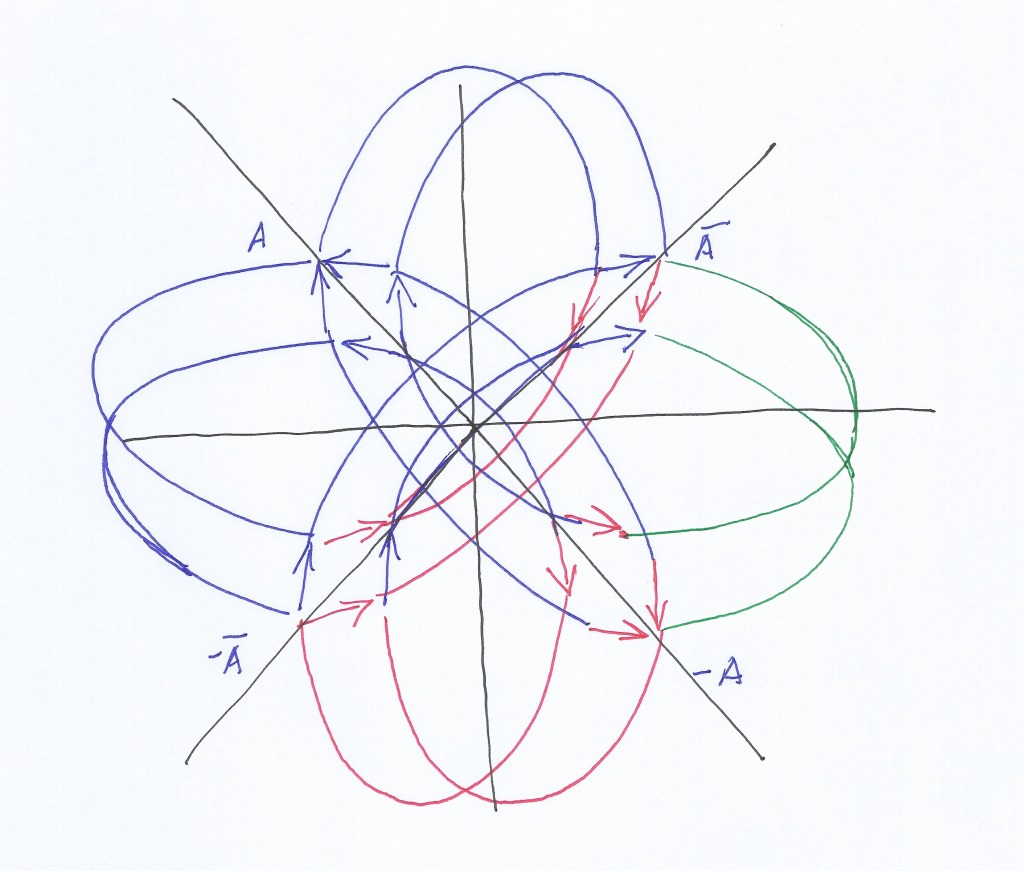
The next gif animation I created does not show how the fermionic particles evolve to become bosons and vice versa. I think also the whole system would rotate around the center of the symmetry. Between each expansion and contraction there will be a moment of no variation, from the instant a field reaches its higher degree of contraction until it starts to get expanded and vice versa, causing a successive prelation. In this sense, any subfield could be its own antiparticle through time when the whole system completes a half rotation.
When it comes to the independent existence of a particle (or if it only exists when it measured) and to local or non local effects, I think when we «observe», when we send a wave that pushes and interferes with any of the two intersecting fields, the whole subatomic nucleus is going to be changed. Because those subfields depend on the behaviour, the phase and frequency of vibration, of the two intersecting fields they are a part from. So we are going to actually change matter when observing it, but that’s nothing to do with uncertainty or indeterminacy, it’s a concrete, causal, and locally determined (with an apparently non local) effect. So it can be rationally explain why if we change the right intersecting subfield, the left subfield is going to be immediately changed.
On the other hand, if we were placed in the concave side of the system, we would not be able to directly detect the anti photon that would appear in the convex side of the intersection. Or if we were placed inside of the left intersecting field, we would not be able to directly detect what is taking place inside of the right handed intersecting field. Those hidden mass and energy would be dark to us.
A fundamental question related to the conception of space is, what does cause the unity of subatomic particles? why do they remain united? what are the strong and the weak interactions in this dual system? I think the chemical bonds that link matter are the inner orbital motions that take place inside of the subfields of the dual intersecting system. Those motions shared by the two intersecting fields make them remain intersected. When both intersecting fields contract at the same moment, the ascending subfield will represent the strongest interaction having a stronger link because of the faster inner orbital motion of the opposite double helix spins; The weakest interaction will take place when both intersecting fields expand at the same moment and the ascending subfield decaes. When it comes to fermions, the weaker interaction will take place at the side of the system where the expanded field is placed and the stronger interaction will occur at the side of the system where the intersecting field is contracted.
On the other hand, when it comes to the cause of the periodic variation of the intersecting fields, I think there must exist a pushing flux (maybe formed by «Higgs bosons» as the term ether is totally forbidden, that are the pushing forces caused by the vibration of the Higgs field); that pushing flux will try to pass through a spatial density, causing the diffractive amplitude of a curvature in the portion of the flux that won’t pass through and a refraction of the amount of flux that passes through, when there’s a higher density. Later, because of the friction, the spatial density will be lower and the curvature will change, getting lower amplitude and larger length, existing less diffraction; the refraction will be lower as well. I think that periodic variable curvature that forms the longitudinal wave would be gravitational. Gravity as a pushing force was already formulated since Newton’s time (Newton himself was aware that a force of attraction was not a causal and mechanical explanation at all) by Fatio, Le Sage, and many others in different ways, until being abandoned at the beginning of the XX when the idea of ether was definitely rejected.
Einstein gravitational curvature does not explain mechanically, outside of the mathematical equations what physically causes the curvature of the field. A mass, density and volume, by itself does not produce a curvature. To curve something a resistance is needed. Although he explain gravity in geometric terms, (Clifford before spoke about the different curvatures of space to explain matter) he could not geometrize electromagnetism as well. Einstein was contrary to the probabilistic view of nature quantum mechanics postulated, but i think he failed in his common sense attempts to rationally explain the atom because of his conceptual idea of space was not enough developed yet. Electromagnetic charges, electronegativity, are not a property that matter essentially owns because of no reason, because that’s its essential nature, it’s the geometric consequence of the displacement of two intersecting fields that vary periodically. The electropositive charge does not move towards left because any kind of opposite force attracts it from there, it moves towards left because of the variation of the intersecting fields that forms produce that displacement.
Periodic variations of gravitational fields have not been measured. Intersecting gravitational fields forming complex multidimensional gravitational subfields fields have not been detected either. But it’s a fact that our current solar system and gravitational models – a part of not being compatible with the quantum mechanical model and the theory of spatial relativity – do not explain mechanically with a unique and same mechanism all the detected asymmetries: different orbital inclinations, different orbital eccentricities, different velocities, and even inverted rotational motions in some planets. Being apparently simple, the apparently random asymmetry of the solar system model reminds the monstruos sculpture formed by the members of different creatures that made Copernicus suspect the geocentric model could not be right. We thought we made a true revolution changing the orbited object but we actually kept unchanged the underlying conception of the unique and invariant space when accepting the heliocentric model without further discussions.
When it comes to the big bang, I think that to guess that celestial bodies are moved by inertia since a remote big bang is another prejudice based on our specific conception of space. From another conception of space I can naturally think planets are moved by the variation of the field they orbit (that maybe even is a blind subfield of the system, in some cases), there will be an inertial motion after receiving the pushing force caused by the field displacement when expanding or contracting. I think a big bang is the pushing force caused by a moving field; it can be the vertical pushing force of the ascending subfield that causes the photon, or the horizontal pushing force caused by the displacement of the electron subfield; and it will be followed by big a silence. Big bangs and big silences will be periodically intercalated. We do not know how many universes or multiverse systems there are, but we can suppose that nature works in the same way, with a same simple mechanism at every levels.
Another model I see is very closed to this approach is the anyons model. 2D models of anyons are being used in topological quantum computation, and it seems also 3D and field models of anyons have lately been tried. Anyons can appear indistinctly as fermions or bosons. Physicists think that happens randomly.
I saw the wikipedia animations about anyons and I did recognize there the trajectory of the spins that take place inside of the bosonic ascending subfield with its double helix spin, and its evolution towards the left or right handed electron or positron subfield, in the model of two intersecting fields.
https://en.wikipedia.org/wiki/Anyon

Particle exchange 2d anticlockwise. Maschen / CC0

Particle exchange 2d clockwise. Maschen / CC0
I represented what to me seems to be similar trajectories in this way long before knowing about anyons, visually considering how the intersecting fields and their subfields would behave while varying. To me it’s evident the above animations lack the whole 3D topology of the system that causes those motions and trajectories. What would be causing those spins? I think the variation of two intersecting longitudinal waves.
On the other hand. When it comes to the transversal subfields, I saw that a similar local emplacement was already used by the Kaluza klein spaces and also by the Kalanui Yau inner spaces used in string theories. The transversal subfields are extradimensional because they cannot be described by using the spatial coordinates we use to describe the two intersecting fields and the orthogonal subfields. (the Y coordinate of a transversal subfield corresponds to the Z coordinate of the intersecting fields). There’s no compactification problem here, that is something the string theory has not solved yet when it comes to spatial extra dimensions. (Bu the way, I do not agree with the notion of the string they use, instead of using wave fields, which I think is limiting their whole model and the main cause they are seriously stuck in the development of it).
Looking for info about anyons I saw some researchers are following as well a topological approach of matter and of quantum computation. This next picture is from the Peter Grunber institute:
And this other below picture is about the Majorana fermion model; such approach is currently being used in the efforts of the developing quantum computation and in topological quantum field theories.
The model was developed by Alexei Kitaev who created a version of the so-called Sachdev-Ye model.
The below intersecting fields picture appeared in an article of Vicent Mourik «Signatures of Majorana fermions in hybrid superconductor – semiconductor nanowire devices»
I think the Majorana fermion in the above diagram – that clearly present two intersecting wave functions – is the central subfield that will move as electron/positron from left to right and right to left when the phases of vibration of the two intersecting fields are opposite, and will evolve to an ascending and descending orthogonal subfield that causes the photon and its decay when the phases of vibration of the two intersecting fields synchronize becoming equal.
We know that the ADN is formed by a double helix, the cigoto or primordial cell is formed but two entangled cells, material elements are measured in nature as diatomic, many solar systems have been detected to be binary, and we see that everything in nature follows the path of mirror symmetry, combining left and right, up and down motions.
Do you think is it natural to think everything depends on a unique and independent wave or field?
I’m starting to read this book of Thomas R Davies and Daniel S Nydick about Lorentz transformations and the Dirac equation:
The font is to small for me, but I felt the first pages were interesting enough:
II got interested about the reference to the Art Hobson Article «There are no particles, there are fields». It has an interesting bibliography at the end of the paper.
Haz clic para acceder a 1204.4616.pdf
Take a look to this initial paragraph to finish this post: «Physicists are still unable to reach consensus on the principles or meaning of science’s most fundamental and accurate theory, namely quantum physics. An embarrasment of enigmas abounds concerning wave-particle duality, measurement, nonlocality, superpositions, uncertainty, and the meaning of quantum states. After over a century of quantum history, this is scandalous«. (I’d also specially add entanglement).
Have a nice weekend.
Regards from Spain

























Escribe tu comentario