Dear friends, how are you?
I changed the blog url coming back to the default wordpress.com direction. That implies Google is punishing the blog in the search results (as now there are in the internet some – not too much anyway – broken links). Sorry for the inconveniences.
Today I’m pleased to introduce you the «Kummer surfaces«:
Images: Claudio Rocchini, CC BY-SA 3.0
I took the figures from Wikipedia: https://en.wikipedia.org/wiki/Kummer_surface
I arrived to this figures by searching about Fresnel’s wave surfaces: «Fresnel’s wave surface, found by Augustin Jean Fresnel in 1822, is a quartic surface describing the propagation of light in an optically biaxial crystal. Wave surfaces are special cases of tetrahedroids which are in turn special cases of Kummer surfaces.»
https://en.wikipedia.org/wiki/Wave_surface
And I arrived to the notion of «wave surface» after watching the first part of this conference about «geometric phases» by professor Michael Victor Berry:
I found very interesting the first part, where professor Berry speaks about the intersection of wave surfaces, and name the points of intersection between two cones as «Hamilton points»
So, I have to say thank you to professor Berry for putting me on the way that drives to the Kummer surfaces. Before arriving to the Kummer surfaces, I wrote an email to professor Berry, because he is an eminence about difference of phases, and so I thought he could understand the model I’m defending on this blog, because it’s all about intersecting waves and phases of vibration that synchronize and desynchronize cyclically, where a difference of phase plays a central role and explains the supersymmetry of the system.
I’m going to paste the email I sent hime below, and before the end of the post I will past the email he replied me.
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Subject: Dual atomic model of two intersecting waves vibrating with same or opposite phases.
Dear Professor Michael Berry,
If you had time, I’d be very pleased to know what you think about the ideas I’m sending to you in this email. I’m not a professional scientist.I think the atom could be thought as a dual topological structure formed by the intersection of two longitudinal waves that vibrate with the same or opposite phases; the subwaves existing in that intersection would be the subatomic particles of the nucleus shared by this dual atomic system.
I guess a unique and independent vibrating wave pilot cannot explain mechanically how the particle is related to its pilot wave, and it cannot explain why the elements of the atomic nucleus remain united, how the strong and weak interactions take place mechanically.
Unconnected parallel worlds or universes cannot mechanically and causally explain the atom either.
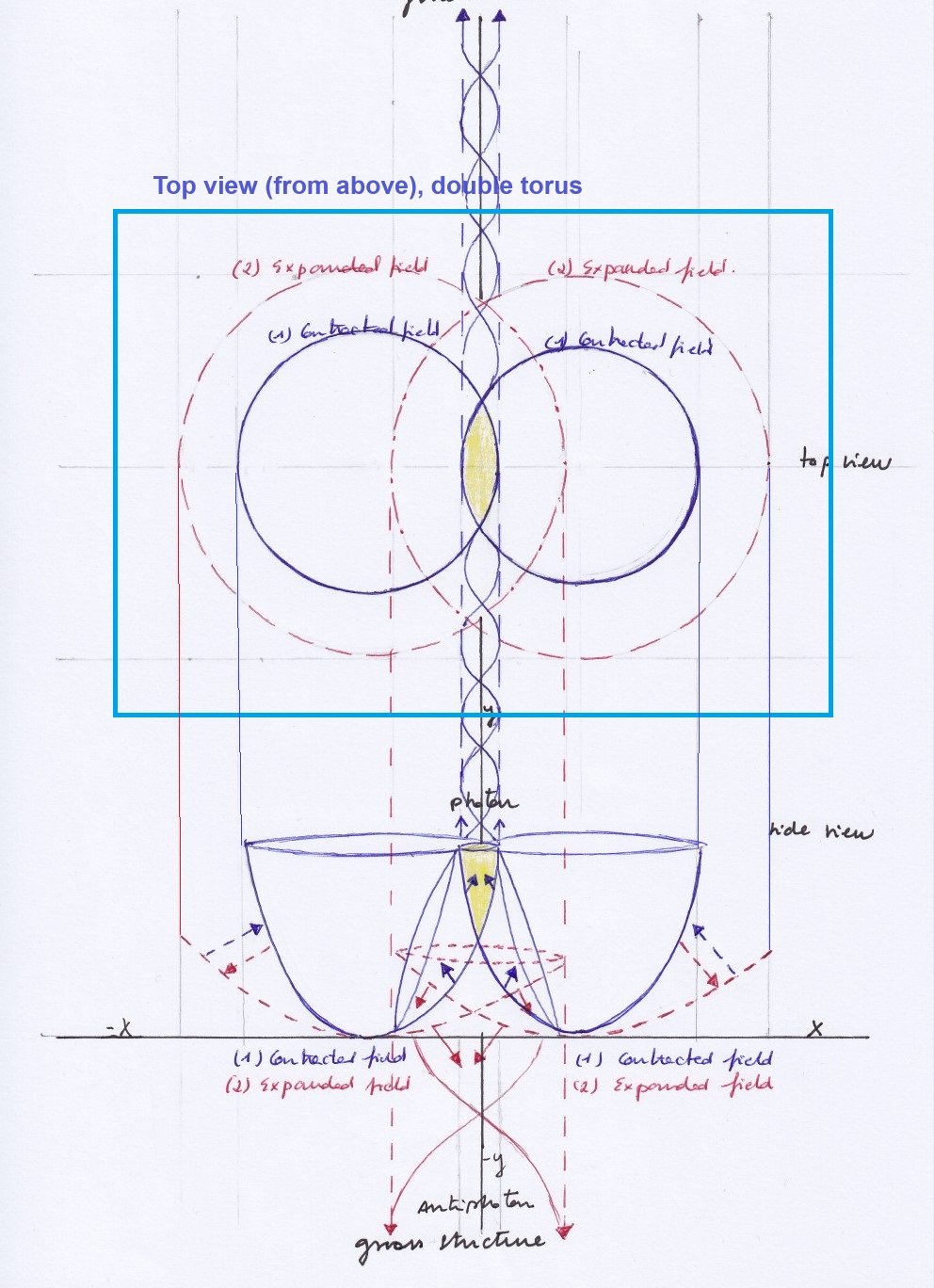
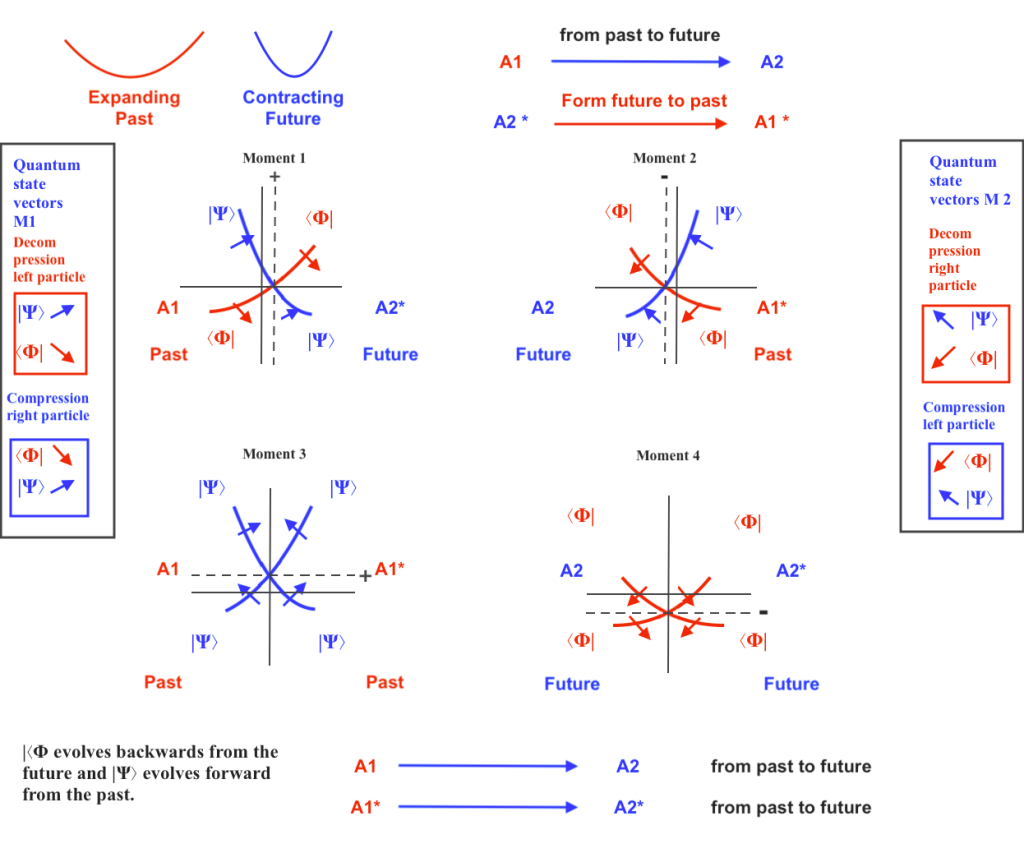
But considering two intersecting longitudinal fields that vibrate, the strongest interaction will occur in the orthogonal subwave when the left and right intersecting waves contract at the same moment, and the weakest interaction will occur when they both expand at the same moment. So the interaction or chemical bond that lets the dual system and its nuclear parts will be the inner kinetic motion that will happen inside of the nuclear subwaves, being faster or accelerated when the subwave is contracted and slower when it’s expanded.
The shape, behavior and physical properties of the nuclear subwaves will be different depending on the phases of vibration of the intersecting waves.
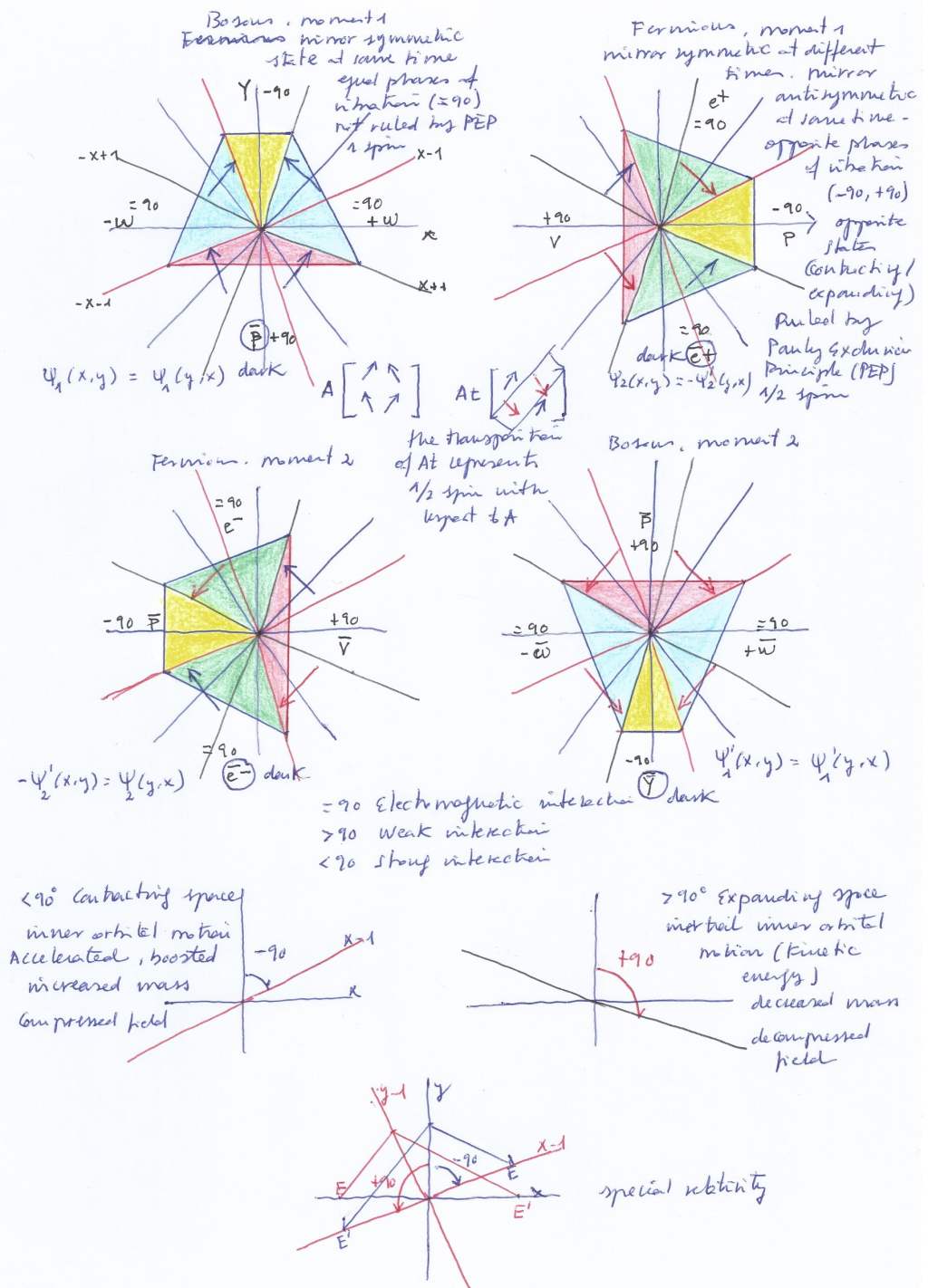
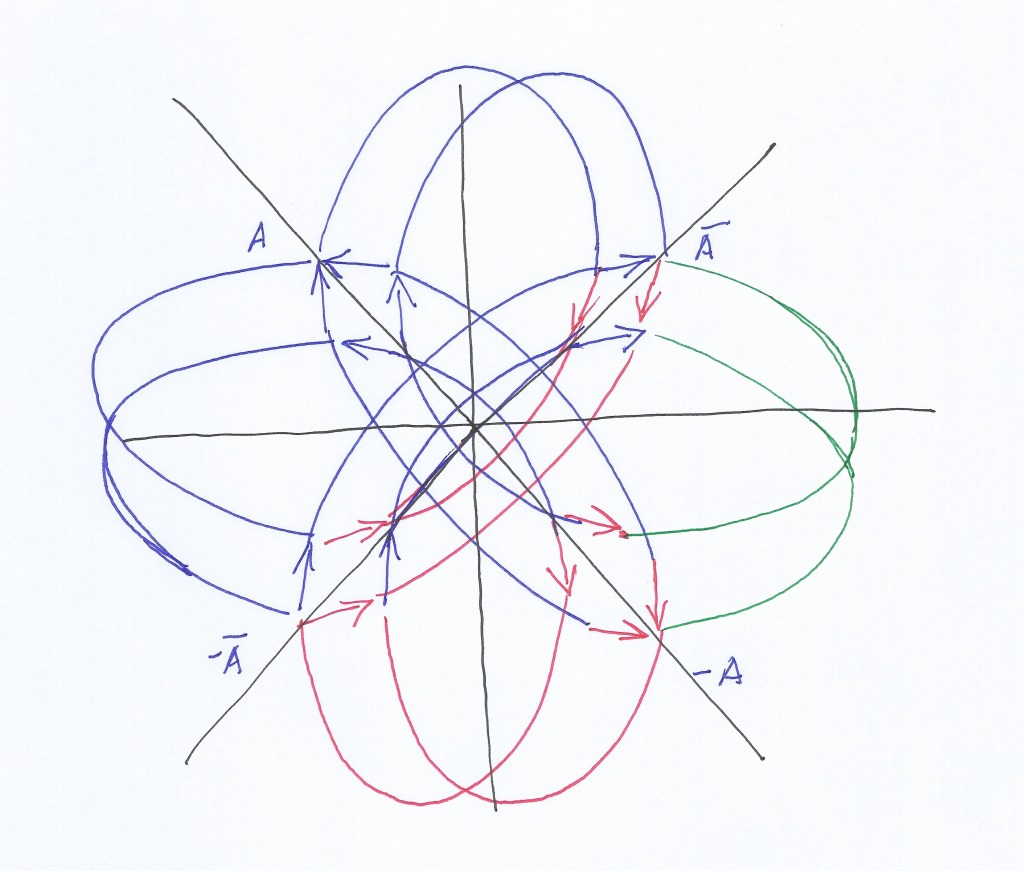
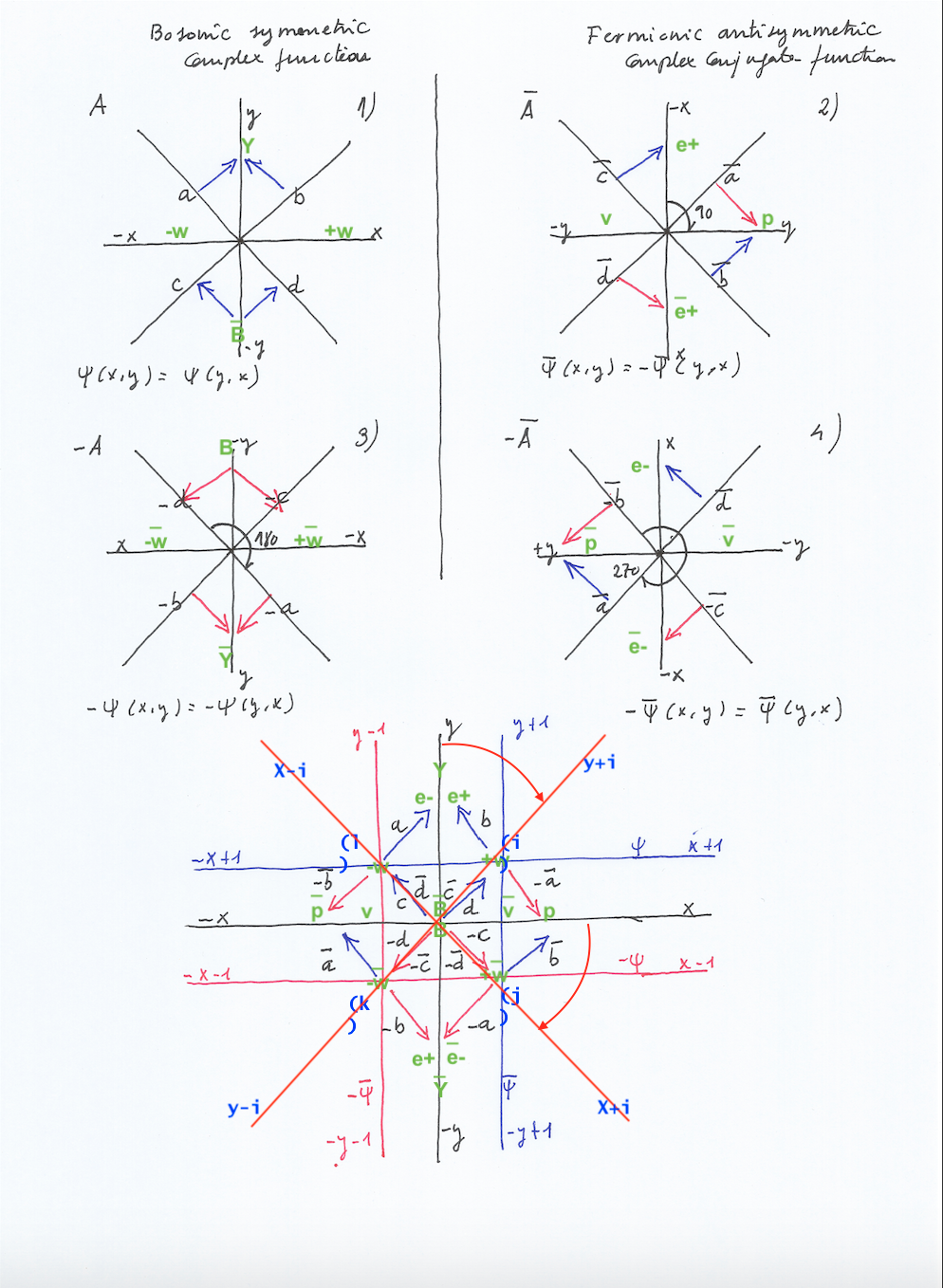
1. When those phases are opposite – when the left intersecting wave contracts the right one expands and vice versa – the orthogonal subwave will move in a pendular way towards the side of the intersecting wave that contracts. When it moves towards left we call it an electron and when it moves a moment later towards right we call it a positron. Electron and positron will be then their own Majorana antiparticles. As the electron and positron cannot exist simultaneously at the same moment (if we will we can speak about a particle a virtual particle that has the potential of becoming existing a moment later) they will be ruled by the Pauli Exclusion Principle, being fermions that should obey the Dirac Fermi statistics, although this model is not probabilistic.
We can think about a double cone if considering the convex side of the dual system as well.
But we also can consider the transversal subwaves as particles of the atomic nucleus. (Inner transversal spaces have already been considered by Kaluza Klein and Calabi Yau models). In this sense, when the left intersecting wave contracts and the right one expands, at the left side of the center of symmetry the transversal subwave will be contracting acting as a neutron while in the right handed side there will be an expanded transversal antineutrino; a moment later, when the left intersecting wave expands and the right one expands, the left contracted neutron will expand becoming a neutrino and the right expanded antineutrino will contract becoming a proton.
In this sense, the neutron and proton will be different transversal subwaves that have mirror symmetry existing at different successive moments; they will be Dirac antiparticles ads the neutrino and antineutrino will, following as well the fermionic Pauli Exclusion Principle.
Here, the space of the subwaves cannot be described by means of the spatial coordinates that we would use to describe the space of the intersecting waves, because they won;t be coincident: the Z coordinate of an intersecting wave will be the Y coordinate of a transversal subwave. And it implies that if we try to describe a rational Y coordinate by using the irrational Z coordinate or vice versa, we are going to get unexpected different measures (because the referential metric of the Z coordinate is larger than the one of the X or Y coordinate).
2. When the phases of vibration of the intersecting waves synchronize becoming equal, the orthogonal subwave is not going to move left to right but upwards and downwards, receiving a double left and right force of pressure when contracting while ascending, and experiencing a decay of its kinetic energy and its pushing force when descending while expanding. When the intersecting waves contract the ascending subwave (with a inner orbital double helix) will cause a pushing force that would represent a polarized photon, and when they expand the descending subwave would represent a beta decay while at the convex side of the system an inverted pushing force will work creating an antiphoton; (if we are measuring the system from its concave side only, that antiphoton will be «dark» for us).
At the left and right side of the center of symmetry there would simultaneously be two mirror symmetric subwaves. As they will exist at the same moment having the same «quantum state» of being contracted or expanded, they won’t be ruled by the Pauli Exclusion Principle and so they will be Bosons that should obey the Bose Einstein statistics.
The left and right transversal subwaves having the same quantum state or phase or vibration and having mirror symmetry at the same moment will represent what is currently named an entanglement; while the left and right transversal subwaves having an opposite quantum state and mirror symmetry at different successive moments will be considered a superposition.
I think superposition and entanglement must be understood in terms of mirror symmetry and phases of vibration.
The left and right subwaves are not a unique «cat» so to speak, but two different cats having mirror symmetry at the same (bosons) or successive (fermions) moments. But if we will we can speak about only a left or right cat that looks at a mirror and sees its own identical (but distinguishable because of the opposite direction of its inner orbital motion) image just in real time (in the case of bosons) or the image it’s going to have a moment later (in the case of fermions). If we think the state of being contracted is equivalent to being alive and the state of being expanded represents to be dead, then we can say that in the case of bosons there are going to be two alive or two dead cats, while in the case of fermions there’s going to be one dead and one alive cats.
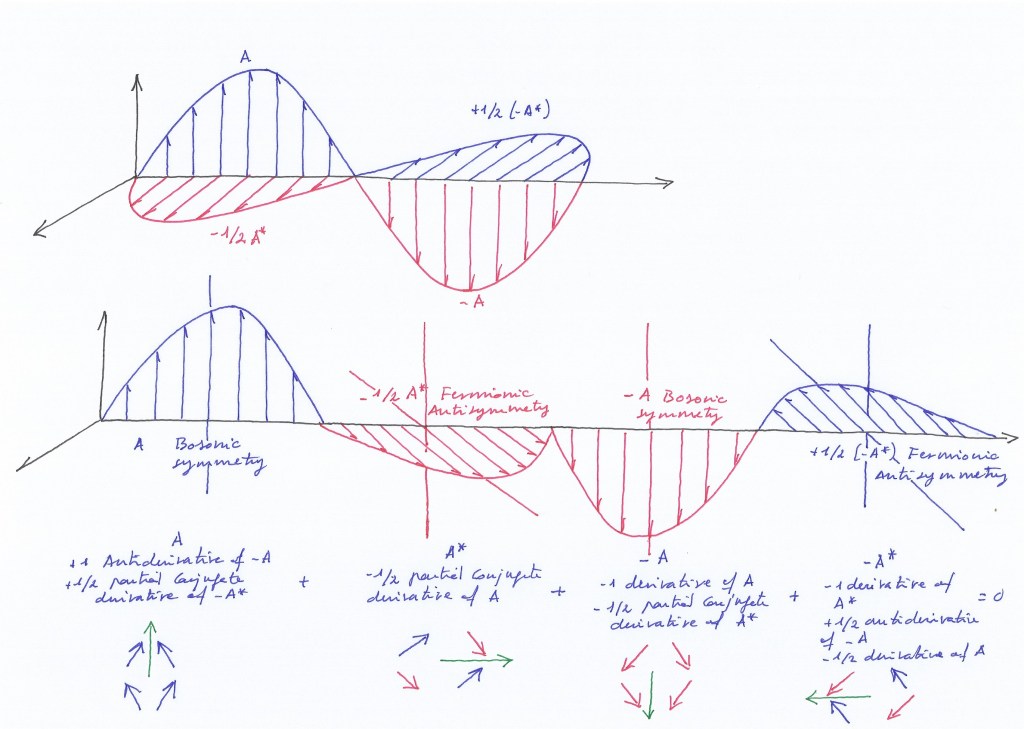
I think the forces of pressure caused by the intersecting waves while contracting or expanding can be represented as vectors and seen as the quarks of the system. Quarks would be the symbolic vector «particles» that would carry the force. And that lets us explain how the system preserves its symmetry though time by means of the inversion of the vector quarks, in a cyclic way.
In this view, we are not thinking only about extradimensional spaces but also about two fermionic time dimensions (when the phases of vibration of the intersecting waves are opposite) that will converge into one time bosonic dimension (when the phases of vibration of the intersecting waves synchronize becoming equal), that later will diverge again into two fermionic time dimensions when the phases of vibration desynchronize, and so on.
It’s necessary to think as well that the whole system would rotate around its central axis. Between each expansion and contraction there would be a moment of no spatial variation (and as a consequence of no time) that would cause a precession of the dynamic of the subsystem.
I think this model should also be applicable at the macrocosmic level. Instead of a wave we can speak about a gravitational field or a universe that expands and contracts periodically. A big bang would be the photonic pushing force caused by the ascending subwave when the left and right intersecting universes contract at the same moment; it would be followed by a big silence when later they both simultaneously expand.
Periodical gravitational variations have not been measured yet. I think gravity is a force of pressure caused by an etheric flux (or a vibrating Higgs field if we will) that passes through a spatial density causing the diffraction and length of the gravitational curvature, and also a refraction of the flux that achieves to pass through; later when because of the friction the spatial density varys, the diffraction and length of that curvature will change, ando so one periodically.
The Copernican revolution implied to continue with a system of a unique, independent and static space orbited around a center, only changing that body placed in that center. Copernicus suspected the geocentric model because it looks like a monstrous sculpture formed by unconnected members of different and unrelated creatures, as it’s to say, because of its unexplained asymmetries. Nowadays we have a very well depicted heliocentric model with many new and mechanically unexplained asymmetries: different orbital ellipses, different inclinations, different velocities, even opposite rotations explained by very speculative hypotheses. Copernicus would question the current heliocentric model as well.
Kind regards from Spain
Alfonso De Miguel
https://curvaturasvariables.wordpress.com
Madrid
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
And this is what professor Barry replied the next morning:
Dear Alfonso de Miguel,
I cannot comment on your theory because it is too far removed from current ideas and fails to reproduce the quantitative agreement with observations of phenomena that are already understood. Equations and numbers are important.
Yours sincerely, Michael Berry
H H Wills Physics Laboratory
Bristol, United Kingdom
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Professor Berry is very reputed physicist and mathematician, fellow of the Royal Society and Sir. He was very kind replying my email, most people I have emailed during these years never replied (which is understandable as well because mine are unsolicited emails.). But the answer of professor Barry seemed very superficial to me, because a theory is too far removed from current ideas does have no value? And in what parts does it fail to reproduce the quantitative agreement with observations? I would be very grateful to anyone who were able to specify me in what specific extents the model fails. Does it fail because it predicts that electrons must be formed as well by quarks, for example? Does it fail to explain the relation between neutrons and protons because it has been measured they have slightly different weight? Is that part really understood by current physic even if it does not let explain the proton decay as it is the current case? Does it fail to explain supersymmetry? But the more surprising thing is that he mentioned that formulas are important. Are not important diagrams? Why did he not recognize the subfields of the model are Kummer Surfaces? And why did he not recognize the transversal subfields are manifolds related to kaluza Klein and Calabi Yau spaces? Is it because he’s not able to think conceptually and visually about quantum mechanics outside of the abstract equations it has been built upon? Is it because he doesn’t have references to compare with? Is the Schrodinger cat understood? Is quantum superposition understood? Is quantum entanglement understood?
Does not prof. Berry know what a Majorana fermion is and how approximate the figures I sent him are to the diagrams some authors are currently working with about that issue?

Image: Vicent Mourik titled “Signatures of Majorana fermions in hybrid superconductor – semiconductor nanowire devices”:
Is not him interested about supersymmetry at all?
It’s Ok.
I arrived to the conference of prof. Berry after having seen a book while I was looking for bibliography about David Bohm, and I found this one, which (I didn’t realize then) is not actually a book of David Bohm by of Arno Bohm. That’s funny.
«The Geometric Phase in Quantum Systems: Foundations, Mathematical Concepts, and Applications in Molecular and Condensed Matter Physics»
https://books.google.es/books?id=ydrzCAAAQBAJ
I already spoke about the pilot wave of David Bohm. Bohm tried to find a causal and local explanation of quantum mechanics and he arrived to his «pilot wave» interpretation, also known as Bohmian mechanics, that arrives to the same probabilistic results of the still mainstream Copenhagen interpretation of Bohr, Heisenber, and Schrodinger. Bohm thought that the particle would be driven or piloted by a wave.
And finally, I had remembered Bohm theory because I watch a video of Sabine Hossenfelder. I’m not a fan of Mrs, Hossenfelder but in many cases she explains things very clearly. I liked this video of her:
It seems David Bohm is going to be trendy very soon, because there’s a movie about his live and work that is going to be released soon:
This is the main page of the film: https://www.infinitepotential.com/
Watching the Sabine’s video it took my attention what she says about empty valleys in the wave graphic:
And then, she mentioned that David Deutchs thinks or explains those empty valleys by means of the notion of parallel universes.
So, I thought that prof. Deutchs could be interested about thinking on intersecting universes instead of parallel universes when it comes to wave pilots. And I wrote him an email. But he did not replied, which is the habitual thing (prof. Berry is a very kind exception).
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Dear professor Deutsch,
I think it could be useful for physicists to consider the idea of two intersecting wave pilots and to think about intersecting (instead of parallel) universes.
You can see some diagrams about the next and some other ideas on my blog: https://curvaturasvariables.wordpress.com/2020/07/25/anyons-majorana-fermions-and-supersymmetric-quarks-in-a-topological-quantum-dual-system/
When two longitudinal waves vibrating with the same or opposite phase intersect, four subwaves will exist in their intersection. The displacement and the physical properties (compression, volume, density, and inner kinetic energy) of those subwaves will be different depending on the phase of vibration of the intersecting wave pilots.In this sense the electromagnetic atom would be a dual structure formed by at least two intersecting longitudinal waves that share a central nucleus formed by the mentioned subwaves.
When the intersecting waves vary with opposite phases, (when the left one contracts the right one expands and vice versa), the orthogonal subwave will have a pendular displacement, left or right, towards the side of the intersecting wave that contracts. This subwave moving left or right will be an electron or a positron respectively, being the same subwave moving towards opposite places at different successive moments, electron and positron would be Majorana antimatter. When the left intersecting wave contracts, the left transversal subwave will also contract becoming a neutron while the right transversal subwave will expand becoming an antineutrino; a moment later, when the left intersecting wave expands and the right one expand, the left neutron will expand becoming a neutrino while the right antineutrino will expand becoming a proton. Neutron and proton (or neutrino and antineutrino) will have mirror symmetry, being Dirac antimatter at different moments. So, as a subwave and its mirror symmetric counterpart cannot exist simultaneously these subwave are ruled by the Pauli Exclusion principle and they should be fermions obeying the Dirac Fermi statistics.
When the phases of vibration of the intersecting waves synchronize, the orthogonal subwave will not move left to right but upwards or downwards. When the two intersecting waves contract at the same moment, the orthogonal subwave will contract (creating a double helical inner motion) moving upwards and creating an ascending pushing force that will emit a pulsating photon; a moment later, when the two intersecting waves expand the ascending subwave will expand experiencing a decay and moving downwards.
In this case, the left and right transversal subwaves will exist with mirror symmetry at the same moment, having the same quantum state of being expanded and contracted. So, they will not be ruled by the Pauly Exclusion Principle, and they should be bosons following the Bose Einstein statistics. But notice that when it comes to the ascending subwave that creates the photon, its mirror symmetric counterpart is not the descending subwave when the decay takes place but the inverted subwave that will exist then at the convex side of the intersecting waves, creating an antiphoton. (If we are measuring the system from its concave side, we will experience the photonic pulsation as a non continuum, as a quantum, and the anti photonic pulsation will be hidden or dark for us. So the orthogonal subwave will be also ruled by the Pauli Exclusion principle (as it, and its dark mirror antiparticle, cannot exist at the same moment) acting as a fermion.
It’s interesting to note that in this model the transversal vibrating subwaves follow the same phase that the vibration of the intersecting waves with opposite phase (when the left intersecting wave contracts and the right one expands, the left transversal subwave will contract and the right transversal subwave will expand). But when the phase of the vibration of the intersecting waves synchronize, it gets desynchronized with respect to the phase of vibration of the transversal subwaves (when the left and right intersecting waves contract, the left and right transversal subwaves will expand, and when the left and right intersecting waves expand the left and right transversal subwaves will contract).
If we think about a transversal subwave as a cat, we can say it will be alive when the subwave is contracted and it will be dead when the subwave is expanded. In this sense, logically, the cat only can be dead or alive. If we detect that the cat is dead and alive at the same moment, we will be measuring two identical but distinguishable (as they will have opposite kinetic energy) cats that will be mirror symmetric at different successive moments. Those mirror symmetric cats will be fermionic. If the left cat and its mirror symmetric cat are alive and dead at the same moment they will be bosonic.
I suspect that «entanglement» is not being correctly understood currently.
On the other hand, considering the two intersecting waves as wave pilots (as they both by effect of their variation, drive the subwave or particle towards left-right or upwards-downwards, and also determine the «quantum» state of being contracted or expanded of the transversal subwaves), the effect caused on the shared atomic particles by the vibration of the intersecting waves can be thought as a local effect.
I also think the model could be expressed in terms of quantum chromodynamics, considering the quarks of the model the forces of pressure caused by the displacement of the intersecting waves when contracting or expanding.
These quarks let represent the system of subwaves as supersymmetric as they preserve their symmetry through time simply by periodically varying the direction of the vector that represents the quarks when the intersecting waves contract or expand and their phase of vibration synchronize or desynchronize periodically.
It could be possible in this sense to speak about two fermionic time dimensions that converge into a bosonic time dimension that will diverge later in two fermionic time dimensions, and so on.
I guess the model of intersecting wave pilots and nuclear subwaves could also let rationally explain the mass gap.
Kind regards from Spain,
Alfonso De Miguel
Madrid
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
I sometimes think like if these people had blindly measured a field and they had developed some differential equations they are very proud about to determine where a kind of erratic «element» travels, usually describing straight lines and rotating around itself, through around 90 minutes from one part to another of something that could be a rectangle, sometimes being stopped at the center, sometimes being stopped on a corner, even sometimes being stopped for a while at seven meters from what could be one side of the presumible rectangle and then, surprisingly, as if an inexplicable randomness acted, the erratic element traveled attracted by some misterios force to the center…
And when you say, wait a moment, have you ever thought about a soccer stadium? Because what you’re speaking about remember very much to what happen inside of that kind of things… and they remain silent. And when you show them a hand made picture of the Santiago Bernabeu they say: «what the bloody hell is this!!! Have you even studied something about physics or mathematics EVER? WHAT ABOUT NUMBERS AND EQUATIONS????»
Photo: Daniel Schroeder (Yaddayadda), CC BY-SA 2.5, via Wikimedia Commons.
Have a great day
Alfonso


















Escribe tu comentario