r’iéa Hoy voy a explicar cómo entiendo yo los grupos de Galois de una manera que se pueda entender, es decir, sin álgebra.
Este post es más bien especulativo y puede que diga alguna inexactitud, es para mí saber si lo que digo aquí es correcto porque los matemáticos no me han dado feedback sobre si estas figuras son, como yo pienso, grupos de Galois o no. (Esto lo digo por si alguien que está estudiando llega hasta aquí en busca de información).
En todo caso, pienso que sería correcto representar así los grupos y extensiones de grupo de Galois. Como la teoría de Galois, (y toda la teoría de grupos posterior, y de hecho toda la matemática posterior incluida la geometría moderna), surgió y se ha desarrollado de forma algebraica y abstracta, nuestros matemáticos no tienen referencias visuales para, sin poder hacer uso de las ecuaciones algebraicas abstractas, decir si estas figuras geométricas (o si se quiere diagramas) representan o no conceptualmente grupos de Galois.
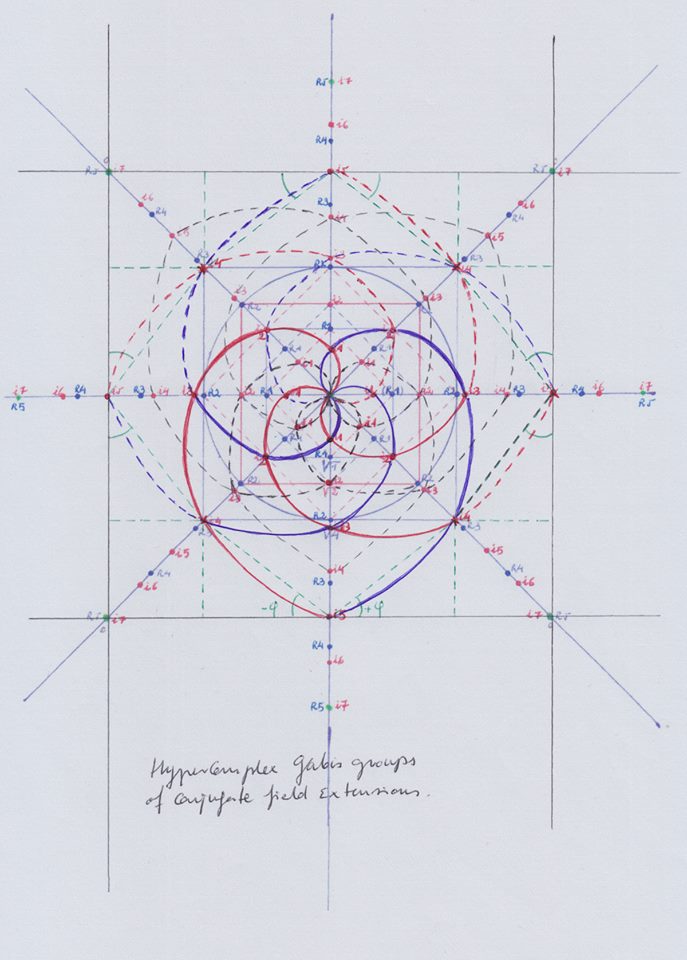
En este post vamos a entender con palabras «cristianas» y paso a paso esta figura, que a mi modo de ver es una representación de grupos hipercomplejos de Galois:
Para entenderla no hay que saber nada de matemáticas. Sólo hay que entender 3 palabrotas de las que usan los matemáticos: «Número complejo», «Extensión» y «Conjugado».
Los matemáticos llaman «número complejo al que tiene una parte «real» y una parte «imaginaria». (Pusieron estos nombres pero podían haber puesto cualesquiera otros).
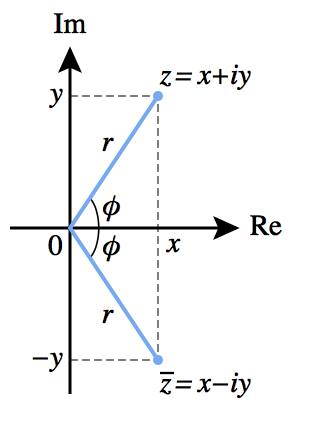
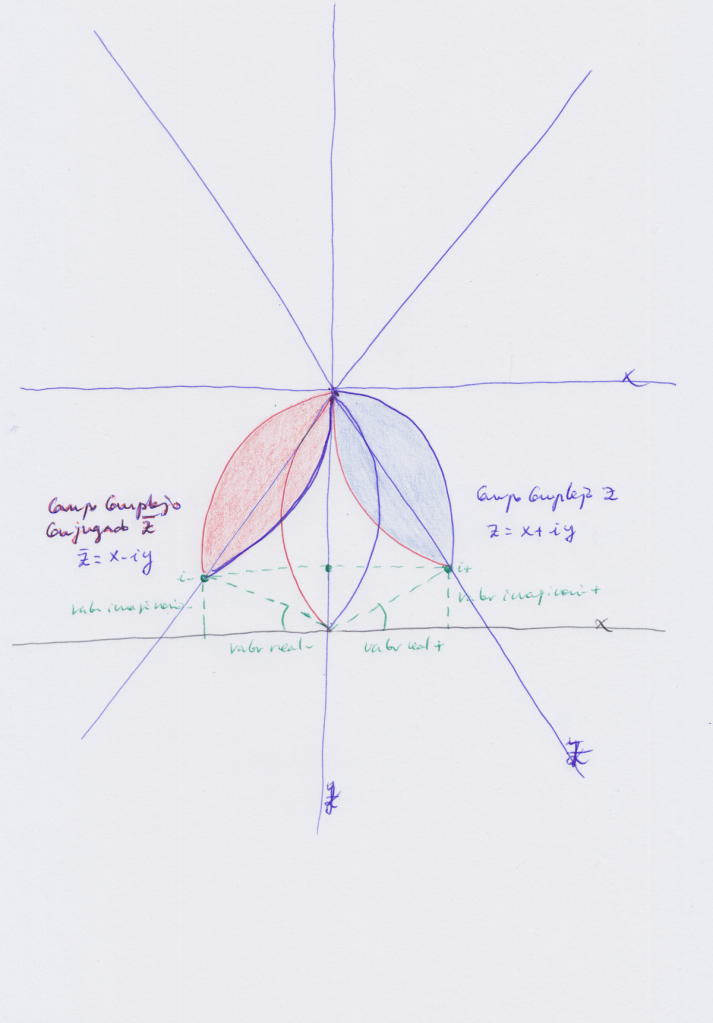
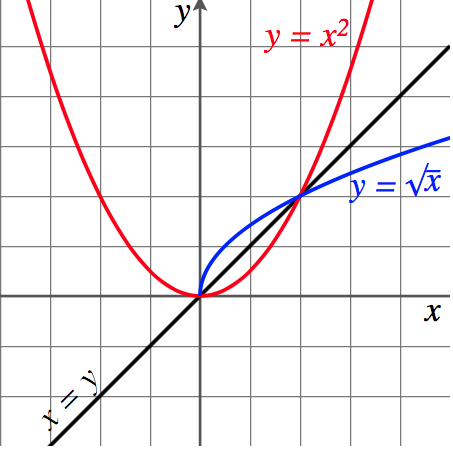
En este dibujo que he cogido del Wikipedia hay dos números complejos en los coordenadas Z, las diagonales, que aquí son las líneas azules: al final de una línea azul hay un número complejo Z y al final de la otra hay otro número complejo Z que tiene un guión en cima:
La longitud o el valor real de esos números complejos de la coordenada Z está en la coordenada X, y su longitud o valor imaginario está en la coordenada Y.
Ya sólo con esto, cuando escuchemos algo de «complejo», «real» o «imaginario», sabemos que se va a estar refiriéndose a una estructura que es como este dibujo.
Por ejemplo, si yo digo: «Ahora voy a explicar los campos complejos de un grupo de Galois», ustedes ya saben que van a ser campos «Complejos» (que se encuentran en las coordenadas Z), y que tendrán una parte real en la coordenada X, y una parte imaginaria en la coordenada Y.
Ahora mismo todavía no sabemos imaginarnos como podrá ser ese campo, pero ya tenemos una idea de cómo va a ser su estructura.
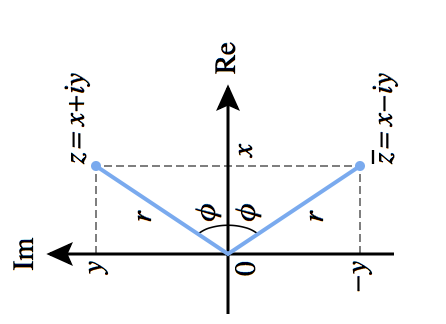
Hay que tener en cuenta que esa estructura básica también puede estar girada (si giramos el plano), por ejemplo así:
O también podría estar girada hacia la izquierda (con lo que variaría la coordenada en la que estaría la parte real y la imaginaria, pero el número complejo siempre estará en Z).
Con este mismo dibujo podemos entender también qué es un campo «conjugado«.
Podríamos decir que en este contexto «conjugado» es aquello que tiene una simetría de espejo con otra cosa que es igual pero opuesta. (Una simetría de espejo se da cuando hay una línea central y lo que está a la izquierda de esa línea, mirando hacia la izquierda, es exactamente igual que lo que está a la derecha de la línea mirando a la derecha, como si ambas cosas fueran una reflejo de la otra).
En el dibujo de arriba podemos decir que la Z de la derecha con el guión encima es el número complejo conjugado de la z de la izquierda. (Al conjugado lo representan con un guión arriba).
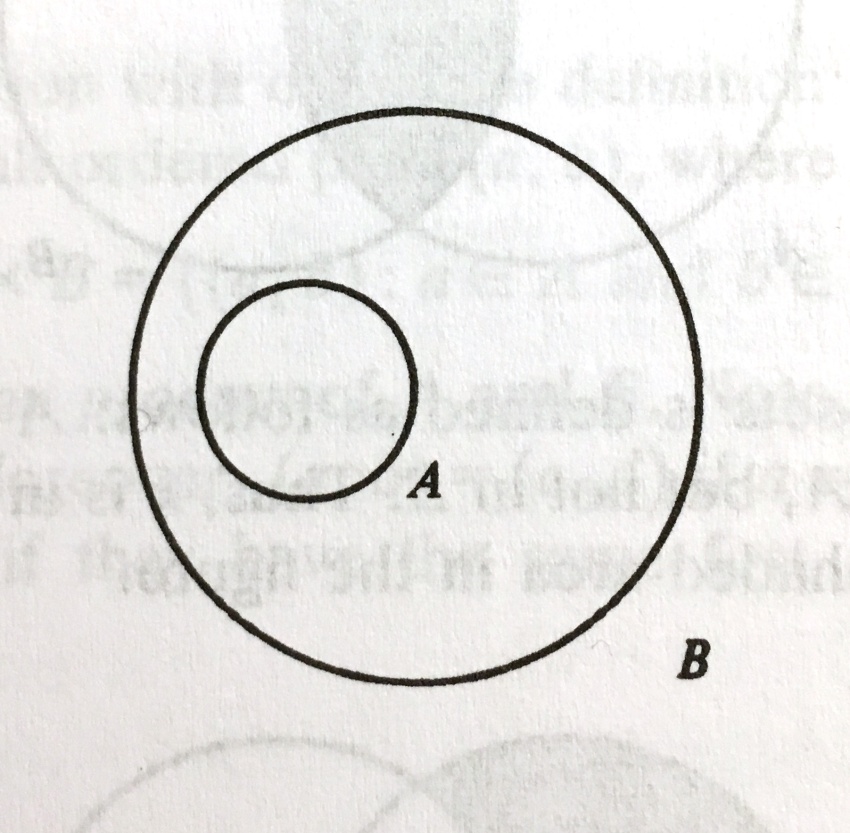
Y ya sólo nos falta saber qué es una «extensión» en matemáticas. Los matemáticos dicen que un campo es extensión de otro cuando este está dentro de aquél. Por ejemplo en esta figura, el campo grande B es una extensión del campo pequeño A. Así de simple. Si B es una extensión de A, entonces se representa algebraicamente con este símbolo B/A.
(Esta figura la he tomado de un libro que se titula «A Book of Abstract Algebra» de Charles C. Pinter).
Entonces ya podemos empezar a ver un grupo de Galois. Un grupo de Galois es un grupo que tiene dos campos conjugados (o sea, dos campos iguales con simetría de espejo, como nuestros brazos, orientados hacia lados opuestos: uno orientado hacia la derecha y otro hacia la izquierda – o uno hacia arriba y el otro hacia abajo). Y además estos dos campos conjugados son complejos, o sea, que van a estar sobre los ejes de coordenadas Z. (No sé si hay grupos de Galois con campos que no sean complejos pero de momento yo sólo conozco estos, que son que he intuido que deberían ser campos de Galois y a partir de ahí he ido haciendo la traducción de términos abstractos a las figuras concretas y viceversa).
Así, en esta figura de abajo tenemos un grupo de Galois formado por dos campos conjugados, uno a la izquierda y otro a la derecha, que son campos «complejos», que recaen en las coordenada Z, que es el punto complejo donde concurren la longitud real de X y la longitud imaginaria» de Y.
Es como si fueran tres pétalos de una flor o tres hojas de una rama.
Entonces, para que quede claro, repetimos los términos: este grupo de Galois es un grupo complejo formado por dos campos complejos (uno a la izquierda y otro a la derecha) y uno no complejo (en el centro). Y el campo de la izquierda es el campo conjugado del campo de la derecha (o viceversa).
(Lo de Z = X + iY no es importante para entender la simetría del grupo de Galois visualmente.)
Como los tres campos son iguales, les llaman «isomorfos». (Los matemáticos tienen estas cosas).
Del campo del centro se dice que tiene una conjugación compleja trivial pero a mi no me parece que sea tan trivial porque este campo es el que determina el punto cero para medir el ángulo de inclinación de los campos complejos conjugados no triviales. Pero entiendo que quieren decir trivial con respecto a lo siguiente que vamos a ver, que es la extensión del campo de Galois, relativa al grupo complejo de Galois, ya que no va a determinar la estructura que va a tener la extensión (a diferencia de los campos complejos conjugados no triviales, que si la van a determinar. Ahora veremos qué significa esta frase).
Ya sabemos que la extensión es un campo que contiene a otro campo. Y en el caso de los campos complejos conjugados de Galois, la extensión va a ser un campo mayor que contenga al grupo de campos de Galois. Al pobre Galois se le deber haber desgastado ya el nombre de tanto usarlo. Aquí todo es GALOIS.
He dibujado la extensión del grupo de Galois con líneas continuas. Así que con la extensión de Galois tenemos un campo mayor que comprende al grupo de Galois.
(Estoy poniendo en rojo las líneas de lado de la izquierda y en azul las del lado de la derecha para representar que también son líneas conjugadas, son iguales, pero miran hacia lados opuestos porque tienen la simetría de espejo. Las curvas pueden representar funciones, y entonces sería una función y su anti función – igual que lo negativo es lo opuesto de lo positivo).
Con la extensión del grupo de Galois hemos creado un campo que es igual que cualquiera de los campos del grupo de Galois. El campo central no marca la estructura de la extensión y por eso pienso que dicen que es trivial.
Teniendo una estructura igual, aunque más grande, también podríamos decir que la extensión tiene isomorfismo con los campos del grupo de Galois, pero en este caso la palabra más precisa sería que tiene homomorfismo con ellos. Isomorfismo se usa cuando se compara un elemento con otro, y homomorfismo sería cuando varios elementos se comparan con otro.
La extensión del grupo de Galois es de un grado exponencial mayor que los campos del grupo.
Y ya está. Ya sabemos que es un grupo (o al menos un grupo complejo) de Galois.
Pero ahora bien… hemos conseguido la extensión de grado exponencial 2 del grupo de grado 1 de Galois prolongando las líneas izquierda del campo izquierdo del grupo de Galois y la linea derecha del campo derecho del mismo. Qué pasa si prolongamos la línea derecha del campo izquierdo y la línea izquierda del campo derecho? Y si prolongamos las dos líneas izquierda y derecha del campo central? Obtendremos dos extensiones más del grupo de Galois? No.
Entonces qué pasa, el grupo de Galois se queda aquí estancado ya? Las extensiones complejas (de la derecha y la izquierda en Z) se quedan a medias sin que se puedan completar? No.
Podemos completar las extensiones complejas pero a partir de un grupo conjugado de Galois. Es decir, necesitamos crear un nuevo grupo de Galois que tenga una simetría de espejo con el primero, o sea que sea igual pero que esté mirando hacia el lado opuesto. Cómo? Así:
Lo bueno es que podemos construir el nuevo grupo de Galois conjugado del primero usando uno de los campos complejos del grupo de Galois anterior. (lo he dibujado a la izquierda).
Entonces, si hacemos las extensiones de los dos nuevos campos del grupo conjugado de Galois, vemos que hemos conseguido replicar en el grado exponencial 2 el primer grupo de Galois. Con la diferencia de que la extensión trivial (el campo extendido en Z) va a ser compleja, mientras que en el grupo 1 el campo trivial está en Y.
Del mismo modo podemos hacer un nuevo grupo conjugado de Galois a la derecha y sacar las extensiones que podremos formar con el primer grupo de Galois.
Ahora las extensiones hacen de nuevos grupos de Galois, y de ellos podemos sacar directamente dos nuevas extensiones complejas conjugadas, ahora de grado exponencial 3.
De la misma forma, prolongando las extensiones complejas conjugadas (en Z) de grado 2, podemos crear la extensión real o trivial (en el centro) de grado 3:
Si prolongamos hasta el grado 4 las extensiones complejas conjugadas y la real de grado 3, conseguimos una nueva extensión real (en Y) de Galois, pero no podemos formar las complejas conjugadas de grado 4 (en Z).
Para completar las extensiones de Galois de grado 4 necesitaremos formar un nuevo grupo de Galois. Y para hacerlo sólo necesitaremos ya solo un campo real (el hueco que faltaba arriba), que formará el nuevo grupo con dos campos complejos conjugados:
Entonces ya tenemos completos 4 campos de grado 1 reales, en XY, y 4 campos en Z. Cuando hay cuatro campos complejos ya se puede hablar de campos «hipercomplejos», que suena todavía más importante. Así que podemos decir que tenemos un total de 8 grupos de Galois de grado exponencial 1, siendo 4 de ellos grupos hipercomplejos de Galois.
Prolongando el último grupo de Galois de grado 1 hasta el grado 4, podemos formar las extensiones complejas conjugadas de grado 4.
Y prolongando las extensiones de 4 grado podemos formar extensiones de Galois 5 grado, que vienen a formar de hecho un grupo de Galois de grado 5, que es isomorfo (que tiene la misma forma) con respecto a los grupos de Galois de grado exponencial inferior.
La teoría de Galois surgió para explicar por qué las ecuaciones de 5 grado no son resolubles con operaciones simples, lo que llaman «con radicales» (suma, resta, multiplicación, división, raíces cuadradas), como ya había demostrado poco antes Niels Abel. Galois se dio cuenta de que los números formaban grupos de simetría y que en las ecuaciones de quinto grado esta simetría se rompía, la estructura del quinto grado era tan enrevesada que no se podía resolver con operaciones simples.
Sin embargo aquí se muestra claramente cómo la estructura de simetría se mantiene en el quinto grado y en los grados superiores, al menos cuando se trata de campos o funciones complejos. Quiere esto decir que una ecuación de quinto grado no admite funciones complejas? O es que no se dieron cuenta de que construyendo los grupos de Galois de esta manera se resolvía el problema de la asimetría en los grados quinto y superior? Será que estas son funciones rotacionales y tampoco se admiten en las ecuaciones de 5 grado? Eso todavía lo tengo que averiguar.
Ahora ya podemos leer cosas sobre los grupos de Galois y entender todo lo que digan que no lleve álgebra.
Un tema muy interesante y que no está resuelto es el del problema de Galois inverso.
Y relacionado con este problema está el problema de la inmersión en la teoría de Galois https://en.wikipedia.org/wiki/Embedding_problem
Y la noción de Restricción de mapa (no sé si la traducción de «Restriction map» que he hecho es correcta, porque el concepto de «map» no está muy claro para mi, yo lo entiendo como molde de replicación, lo que va a determinar la estructura de la extensión).
Lo que se pregunta el problema de la inmersión es si una extensión de Galois puede ser inmersa o incrustada (yo pienso que también de podría decir «embebida» del término ingles «embedding») en una extensión de Galois de tal manera que obtengamos el mapa de restricción entre los grupos de Galois correspondientes.
Para mí, la respuesta a esta pregunta, como ya hemos visto más arriba, es sí. sí, al menos para los casos de grupos complejos o hipercomeplejos de Galois. Porque cada grupo formado por extensiones conjugadas de Galois va a ser el grupo de Galois de la siguiente extensión de grado mayor. Y el mapa de restricción va pasando de los grupos de Galois a su extensión, y de los grupos de extensiones a su nueva extensión, y así sucesivamente. Pero para tener grupos de extensiones de Galois necesitaremos tener grupos conjugados de Galois que completen las extensiones.
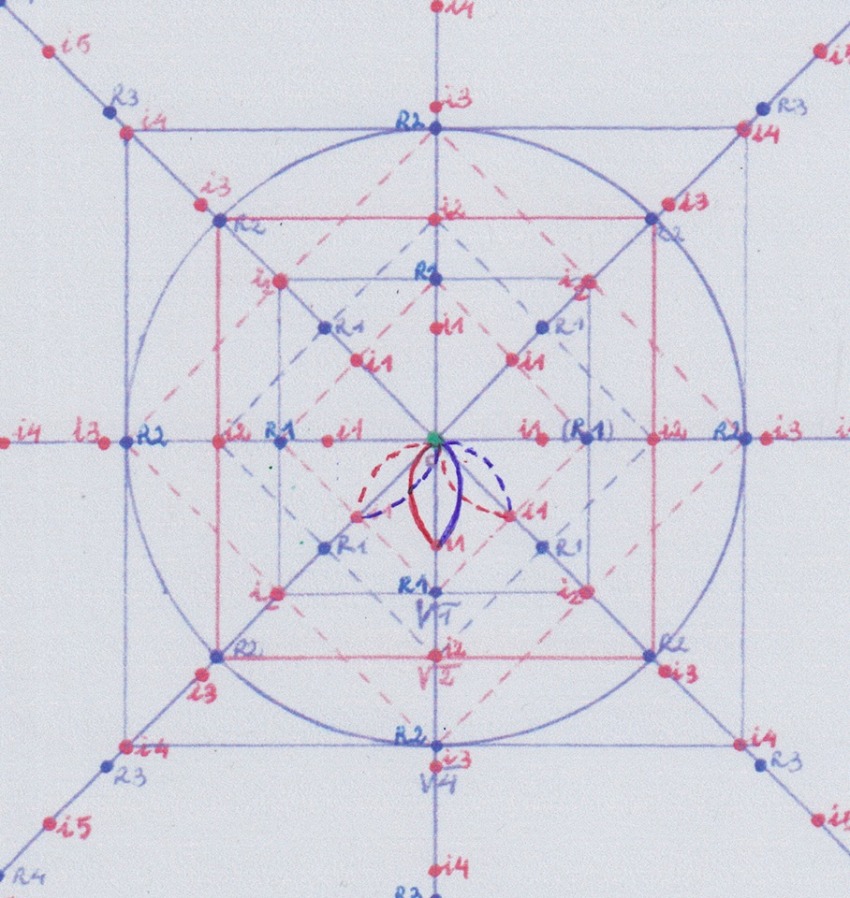
Esta imagen la he tomado del artículo de Wikipedia sobre las restricciones de mapa:
Aquí la curva roja (que representa una función) está determinada por la forma y la situación de la curva roja pequeña que converge con la curva pequeña azul. Eso es lo que va a determinar la estructura de esa función y por eso se puede decir que la restringe.
Ahora ya sabemos entender qué son los grupos y extensiones de Galois – al menos cuando se trate de números complejos. Entonces si leemos esta pregunta (la he tomado de la web mathematical exchange) vamos a saber qué dice. Si esta persona tuviera una imagen visual y concreta de lo que es un grupo de Galois no habría hecho esta pregunta porque la respuesta es obvia: «Suppose P is an irreductible polynomial in Q, with exactly two non-real roots. Then we know these roots must be complex conjugates. Why must be complex conjugation be an element of a Gal(P)?
Nosotros no sabemos qué es un polinomio irreductible, pero sí sabemos que cuando los campos de Galois (o sus raíces cuadradas) son no reales, es decir son complejos (con una parte imaginaria y una real) tiene que estar en las coordenadas Z y ello implica que ban a tener la misma simetría mirando hacia el lado opuesto, es decir que son conjugados. Es así porque es justamente la forma en la que esos dos (tres contando el conjugado trivial del centro) campos conjugados que forman la simetría del grupo de Galois que va a servir como mapa de restricción de la extensión del grupo.
Por otra parte, en español parece que se el término inglés field se ha traducido como «cuerpo» en vez de «campo». «Cuerpo» parece un término más general, más indeterminado, algo que vale un poco para referirse a cualquier cosa que esté allí. Algunas personas me han dicho que un grupo de Galois no tiene ningún campo (porque yo me refiero a los campos – cuerpos si se quiere – del grupo de Galois). Que un grupo de Galois es un «grupo de automorfismo» de la extensión de un campo, de manera que mapea cualquier subcampo a otro subcampo (o a él mismo).
Pero qué es un automorfismo? Wikipedia nos dice que «In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.»
De manera que se supone que un objeto es capaz de crear una imagen de sí mismo, de replicarse o clonarse podríamos decir, en otro objeto que tiene su misma estructura.
A mi me parece que es un contrasentido hablar de la extensión (que es un campo o cuerpo o conjunto) de un subcampo o subcuerpo o subconjunto, y de los subcampos etc de este, y hablar de forma abstracta de un grupo de Galois, que es un grupo de campos y subcampos (o al revés, de campos y de extensiones), y no llamar a esos campos campos del grupo de Galois. Si dicen que no hay campos es porque nunca han visto representado visualmente.
Y si hablan de automorfismos me parece que no están considerando los campos complejos, porque las extensiones no se forman por sí mismas o desde solo un campo o cuerpo que contienen.
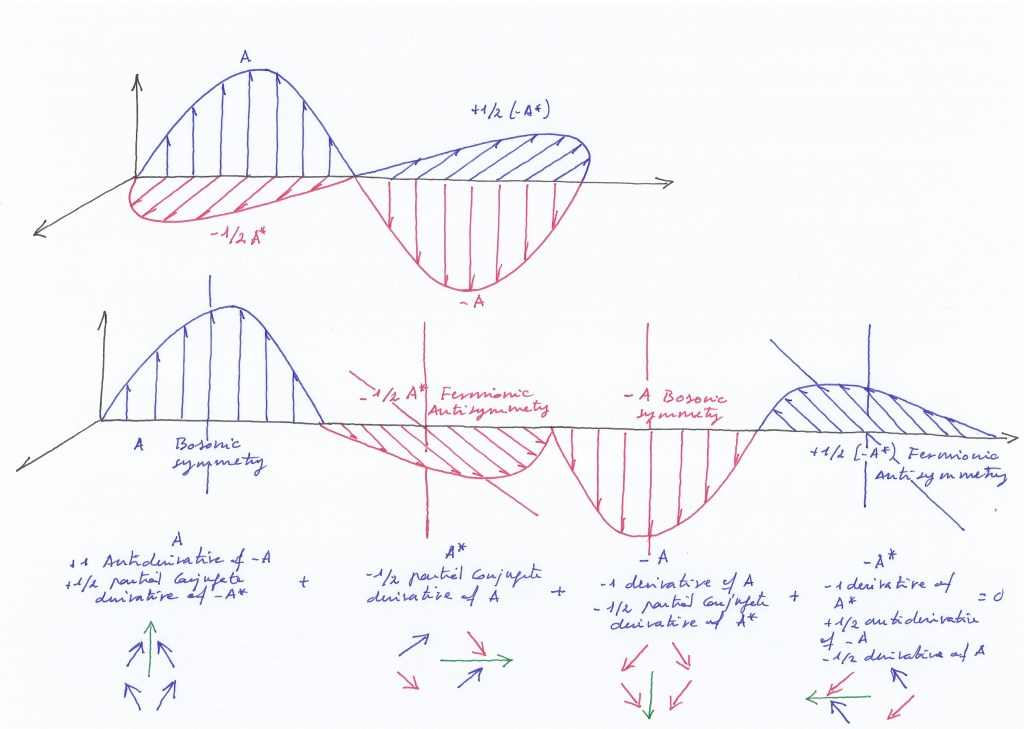
Incluso si vemos la primera figura de arriba, el primer campo que construimos desde el punto cero a partir de una curva positiva y una curva negativa que convergen (lo que podrían ser, creo que lo llaman así, dos «funciones conjugadas») es un campo compuesto por dos partes antisimétricas que forman un campo único en Y. Y de él podemos formar sus dos campos complejos en Z. Pero ya la primera extensión en Y del campo primero en Y no se forma por la prolongación de ese campo primero en Y, se forma por la prolongación de sus dos campos complejos en Z. Entonces esa extensión en Y es un isomorfismo del campo primero en Y, pero pienso que no es un automorfismo porque no está construida directamente desde el campo primero en Y sino desde su desdoblamiento en sus campos espejo en Z.
Estas disquisiciones son importantes para luego poder entender y discutir lo que están diciendo los matemáticos porque ellos, desde las ecuaciones algebraicas han estudiado las simetrías de las estructuras con las que trabajan y las han clasificado en base a estos conceptos de isomorfismo, homomorfismo, automorfismo, y otros muchos que manejan.
Vamos a ver estos dos párrafos que he tomado de este trabajo: https://www.uam.es/personal_pdi/ciencias/fchamizo/libreria/fich/APalgebraII04.pdf
Aquí se nos dice que el grupo de Galois es el conjunto formado por todos los automorfismos del cuerpo contenido en la extensión.
Dada una extensión L / K (o sea un campo llamado K que está dentro de un campo mayor llamado L. L es la extensión de K) se dice que L es un automorfismo que deja fijos los elementos de K (sus imágenes) en L. Si tenemos G(L/K), es decir, un grupo de Galois de la extensión L del cuerpo K, y resulta que H es un subgrupo de G(L/K), entonces H’ tiene que ser un subcuerpo de L que contiene a K (a su imagen de K).
Esto yo lo representaría así, mediante el uso de los campos espejo:
Otra cuestión que se plantea es la relativa a las «permutaciones». Y pienso que una solución alternativa puede darse con los campos, grupos y extensiones espejo, o conjugadas, o antisimétricas, como se quiera decir. (El texto dentro de la llave lo he tomado del mismo trabajo antes mencionado):
Mencionar que en este post he utilizado 247 veces el término «Galois».
Tengan ustedes un feliz día.
Actualización. 6 Mayo 2021
Otra aproximación similar a la representación de los grupos de Galois es distinguir si partimos de una cuerpo inicial de dos funciones opuestas que se intersectan en alguna de las coordenadas X o Y, o si el cuerpo inicial se encuentra en alguna de las coordenadas Z.
Si está en la coordenada X se representaría así.
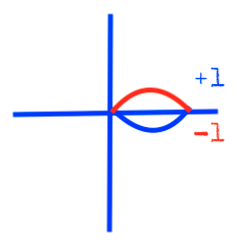
Si rotamos (permutamos) cada una de estas dos curvas podemos formar cuerpos mayores que serán extensiones unos de otros, y todo el grupo será extensión del cuerpo inicial de la coordenada real X.
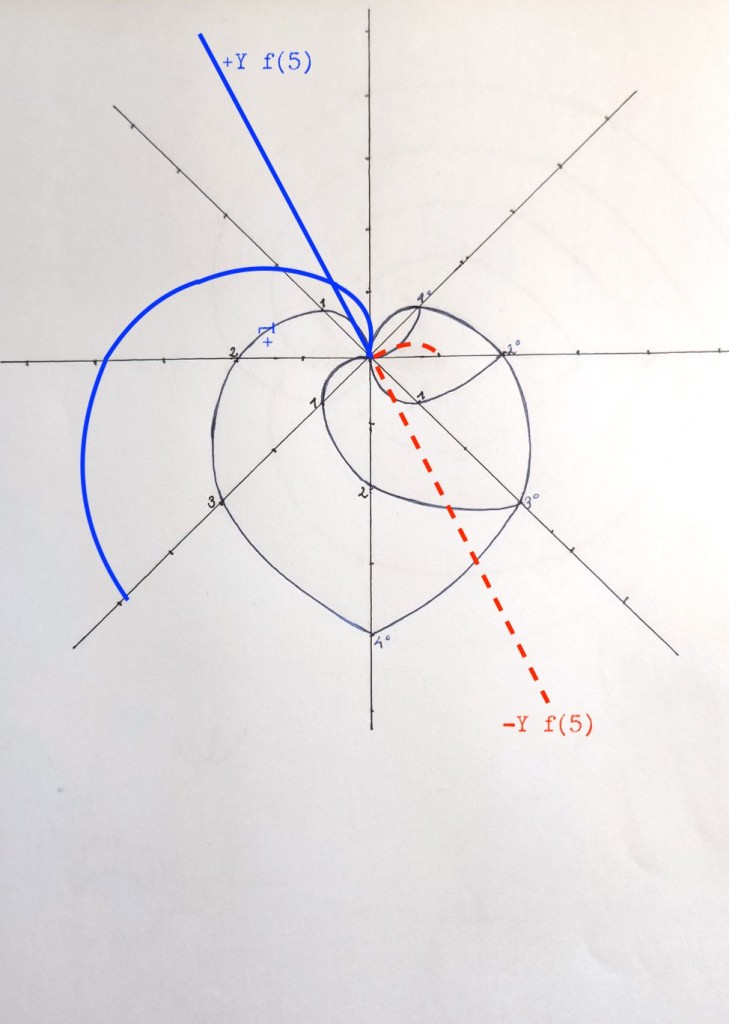
Las extensiones de grado 2, 3, y 4 van a tener una misma simetría, pero cuando llegamos a la de grado 5 (la curva roja en la siguiente figura) vemos que en el lado izquierdo se forma un nuevo cuerpo de grado -1, que es de signo opuesto al cuerpo inicial de grado +1
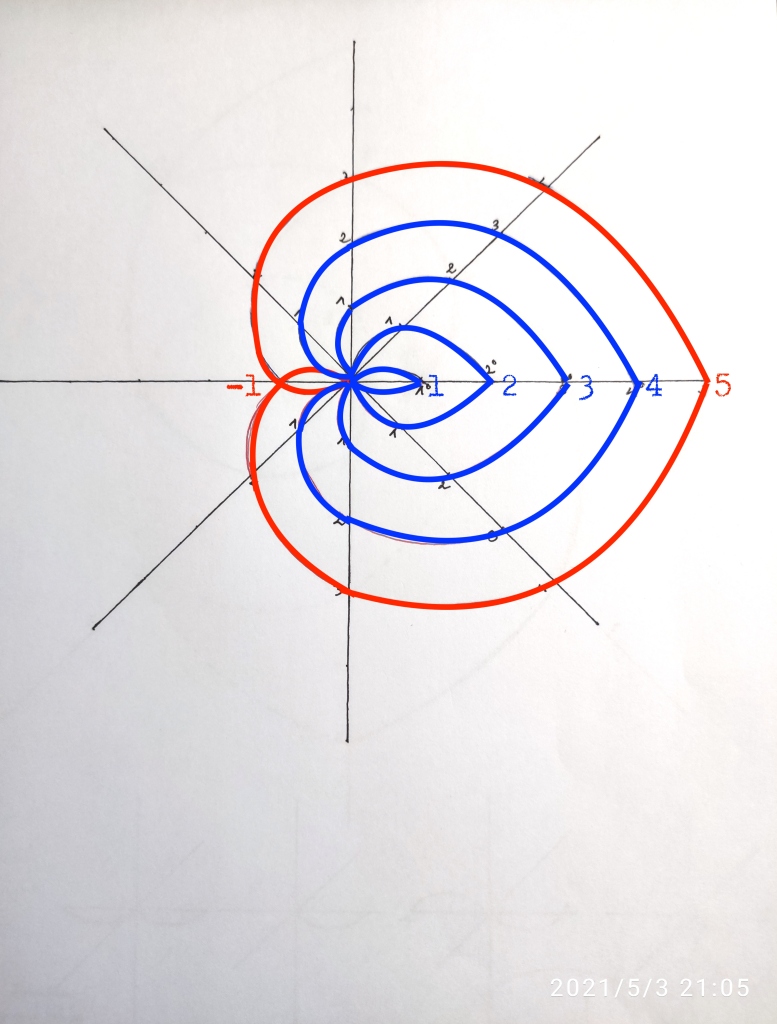
Ello supone que las dos funciones que forman la extensión de grado 5 no se intersectan en el punto cero, como hacen las extensiones de grado 4, 3, o 2, sino que cierran la extensión en el punto -1. Pienso que esta sería una asimetría porque los cuerpos de grado 2, 3, y 4 sólo son extensiones del cuerpo +1, mientras que el cuerpo de grado 5 es extensión del cuerpo +1 y del cuerpo -1.
Podríamos tratar de solventar esta asimetría creando una función de grado 5 inversa, que parta del punto +1, prolongando las dos funciones de grado 1 que forman el cuerpo +1:
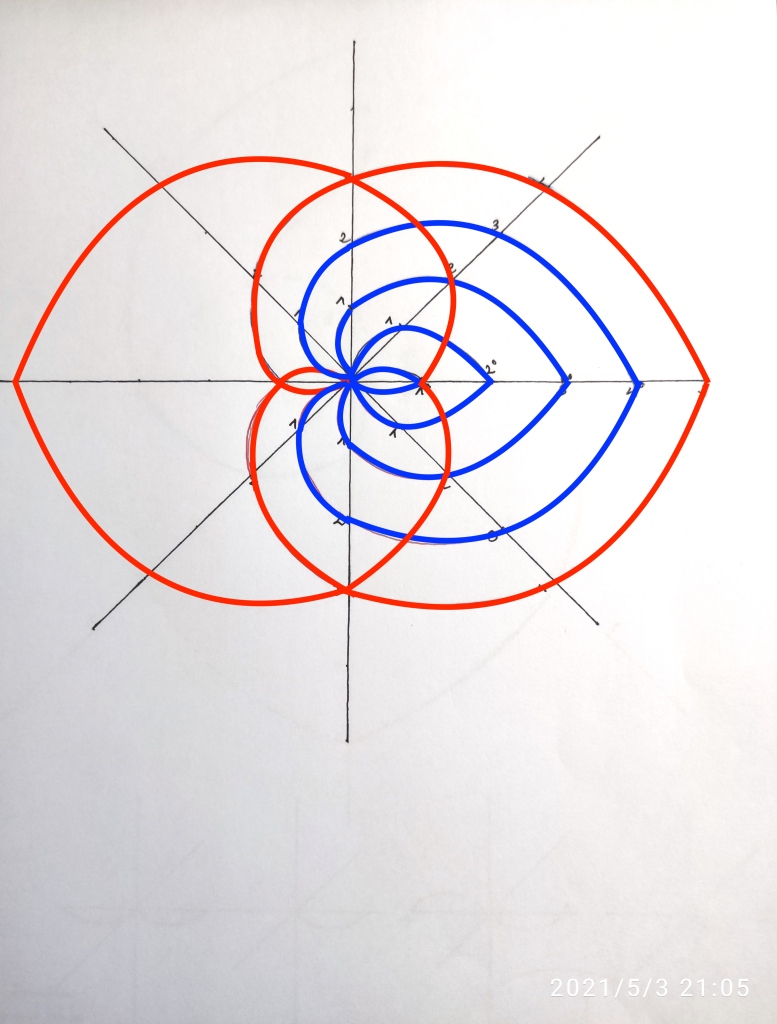
Aquí hemos resuelto la asimetría de la función de grado 5. Pero ambas funciones de grado cinco seguirían siendo asimétricas respecto a las de grado 2, 3, 4. Aunque en la figura anterior vemos cómo al intersectarse las funcioens de grado 5 en rojo con las funciones de grado anterior en azul, se forman nuevos subcuerpos:
Pienso que a las extensiones que formamos proyectando o prolongando las curvas iniciales podrían relacionarse (iba a decir identificarse) con lo que en álgebra llaman ‘proyecciones algebraicas’, y que estos nuevos cuerpos intermedios que se han formado con las intersecciones de estos tipos o grupos diferentes de funciones serían ciclos de Hodge.
Pero aún podemos progresar en la formación de la simetría de la estructura, creando en el lado izquierdo nuevas extensiones de grado 2, 3, y 4, esta vez extensiones del cuerpo inicial -1:
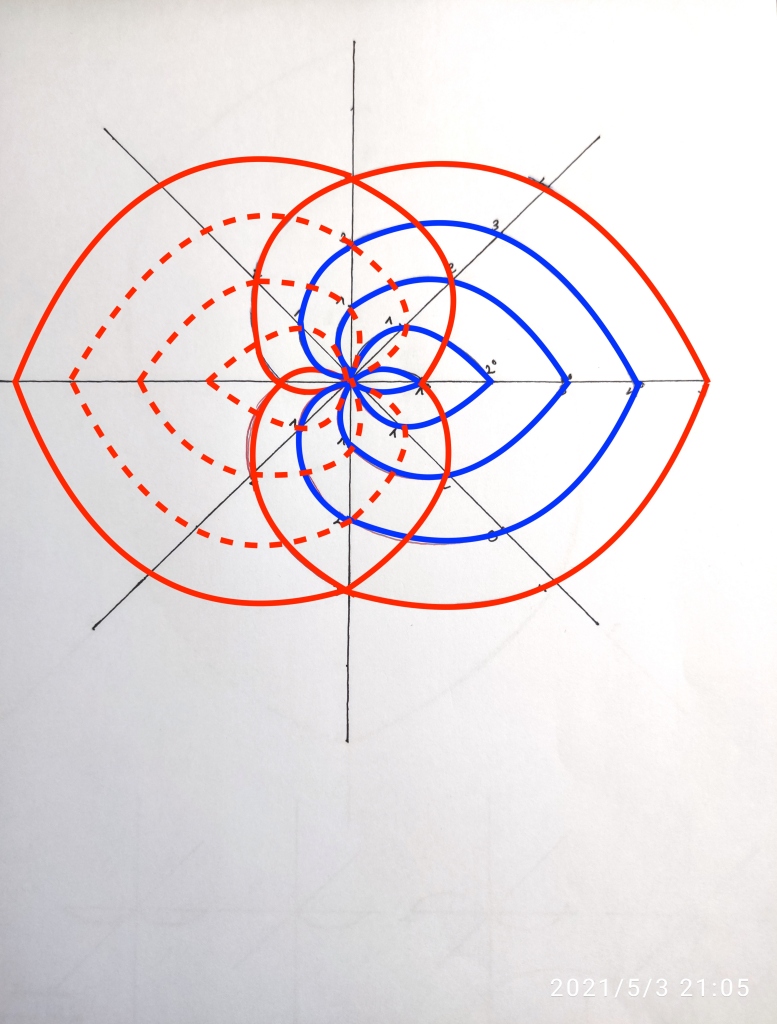
Resuelve esto la diferencia entre grupos? Hemos hecho simétricas todas las funciones? Cuántas funciones se necesitan para resolver con radicales una función de 5 grado, sólo una? Por qué?
En cualquier caso, no sé si se habrán dado cuenta que hemos creado un nuevo sistema de ecuaciones de 1, 2, 3, 4 y 5 grado que sí forman parte del mismo grupo de simetría.
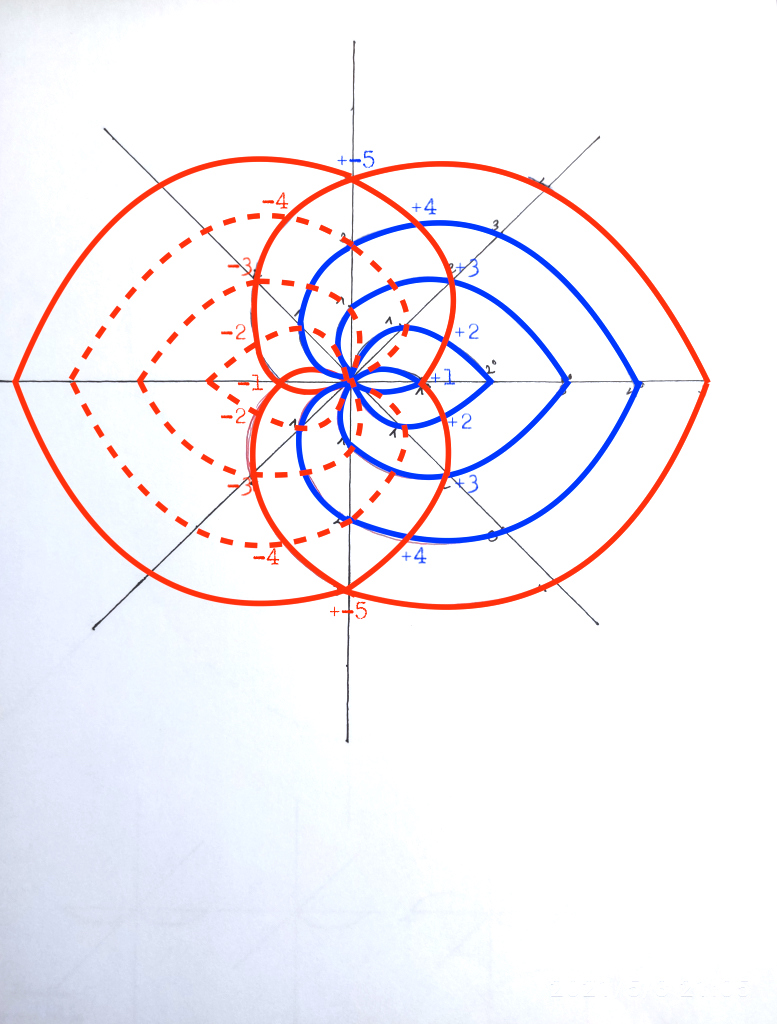
Nótese que en la figura se han creado ya 8 cuerpos de grado 1.
La simetría que comparten estos grupos es, pienso, la de ser ciclos de Hodge; y está formada por dos extensiones conjugadas complejas (hacia derecha e izquierda) y una neutra (intermedia); así, partiendo de dos cuerpos complejos de grado 1 se forma la extensión 2; partiendo de dos extensiones complejas conjugadas se forma la extensión 3, y así sucesivamente, hasta llegar a dos extensiones complejas que forman la extensión 5.
Pero al llegar a las dos extensiones de grado 5 ya no son extensiones complejas sobre coordenadas Z sino que su eje de simetría está construido sobre las coordenadas reales Y. Y al prolongarlas, lo que obtenemos son otras dos extensiones de grado 5 con eje en las coordenadas X, respecto de las cuales las dos extensiones 5 de las coordenadas Y (y también todas las extensiones intermedias complejas de grado menor) son subextensiones.
Pienso que este tipo de espacios serían también espacios de Riemann, que son espacios divididos en subespacios.
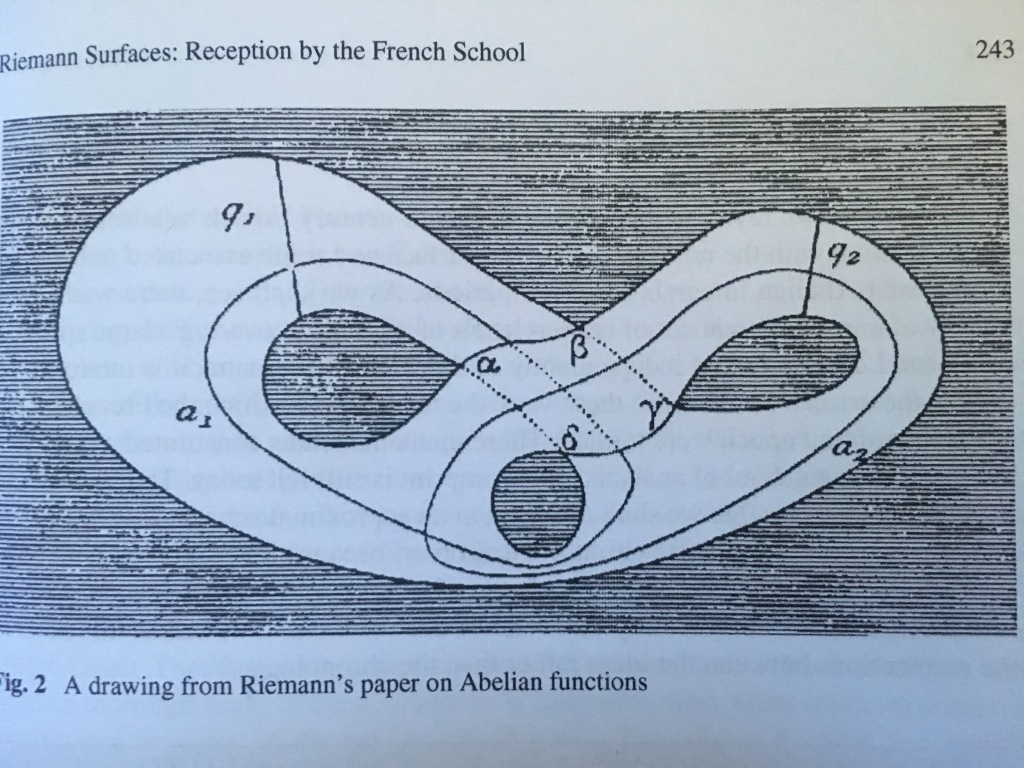
Obviamente, este tipo de simetrías tienen que ser archiconocidas por los matemáticos, pero las conocen de forma algebraica, abstracta. Si no, se estarían usando diagramas de este tipo para explicar los grupos de simetría y, muy sorprendentemente, no se está haciendo.
(De hecho, el problema de la conjetura de Hodge radica en que se han desarrollado algebraicamente estructura cuya geometría se desconoce, y ahora quieren saber a qué geometría se refieren esos ciclos de Hodge).
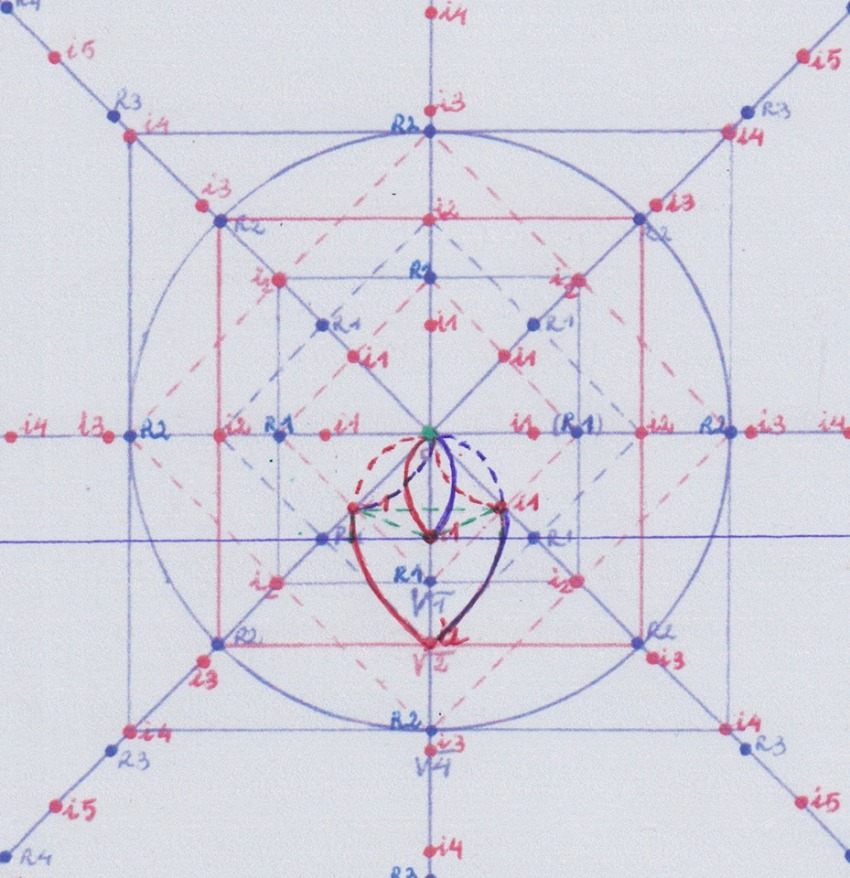
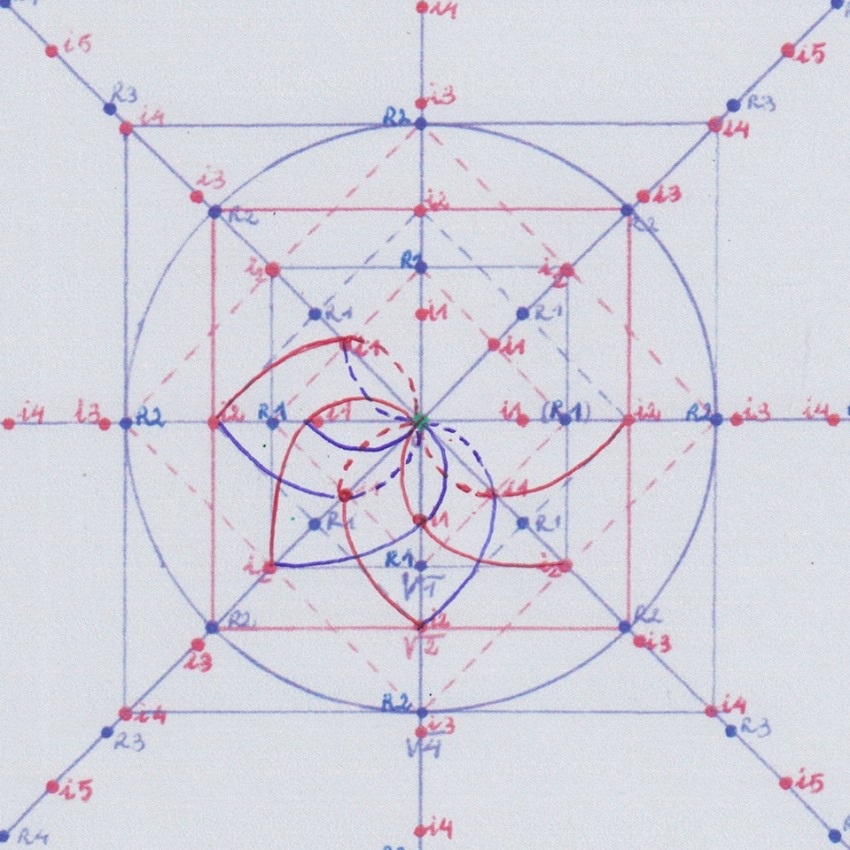
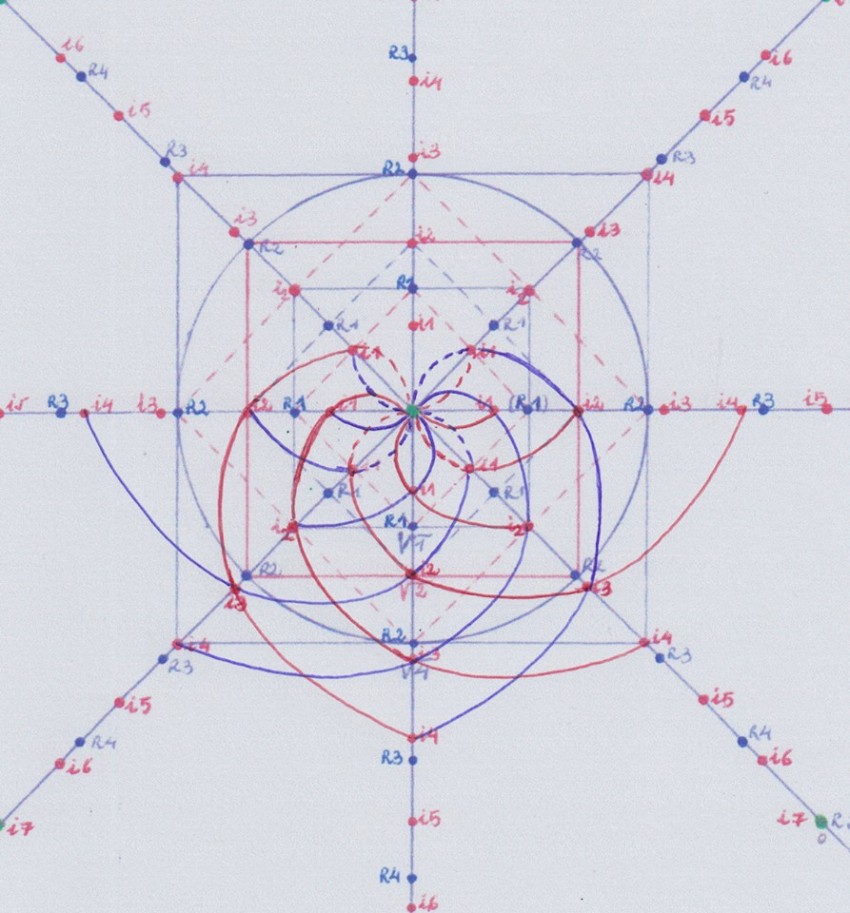
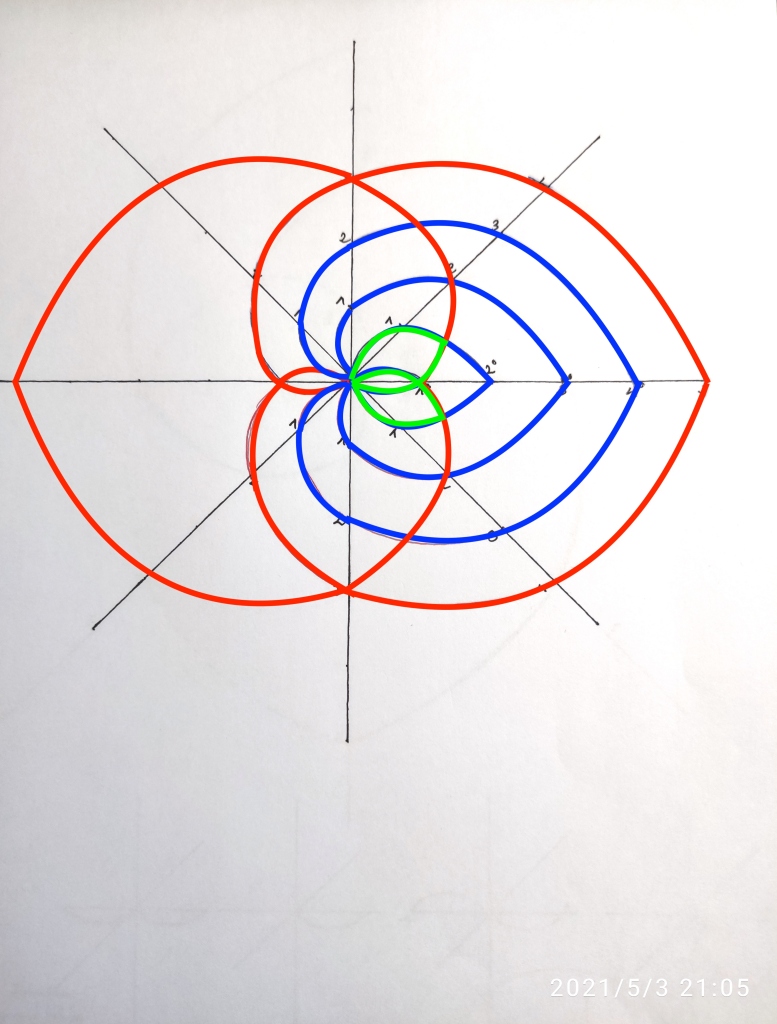
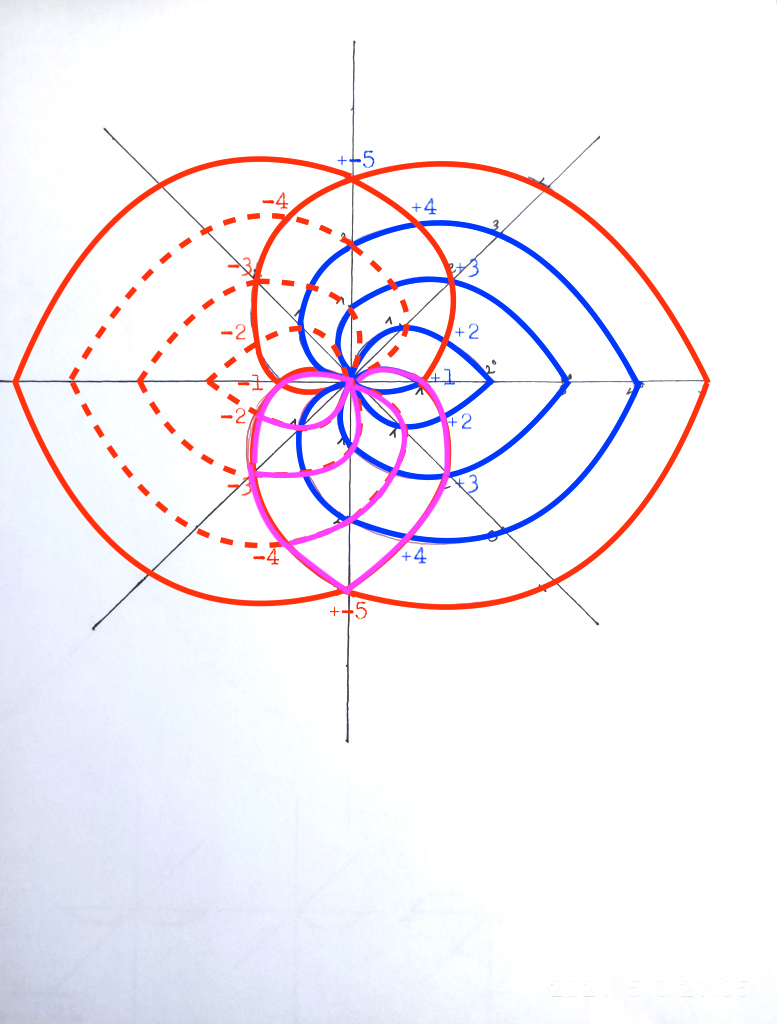
Otra forma de representar el problema de los grupos de simetría de manera similar a como se hace en el post es usando permutaciones en las coordenadas Z complejas, de la siguiente manera:
Hasta la extensión de grado 4 las estructuras o extensiones del cuerpo 1 siguen el mismo tipo de simetría:
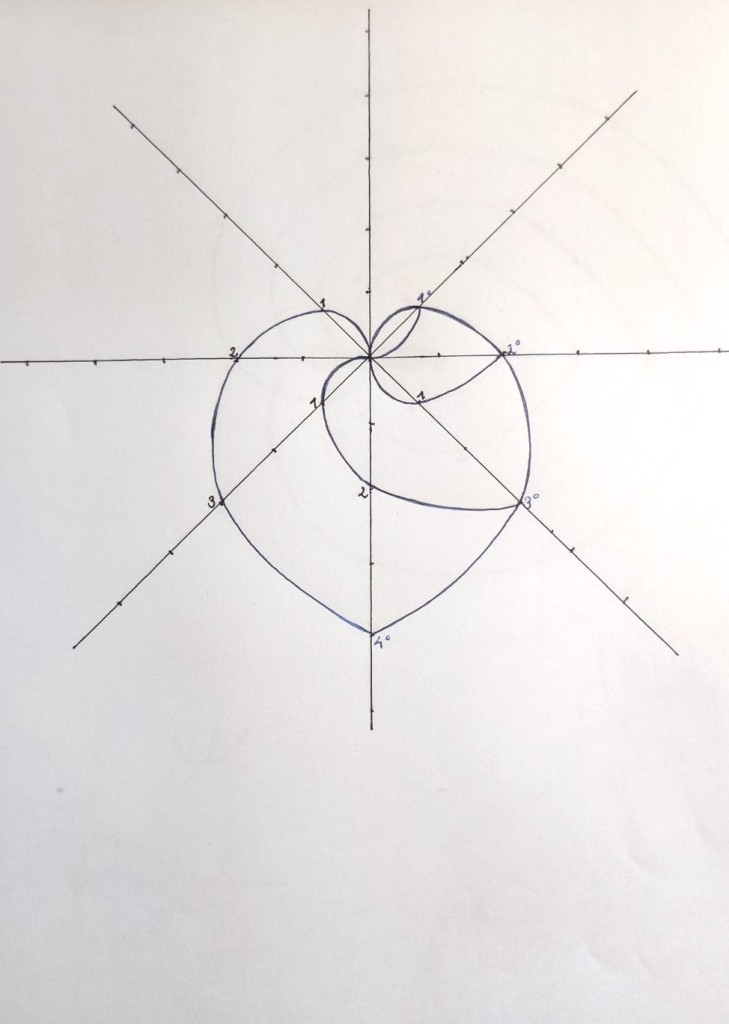
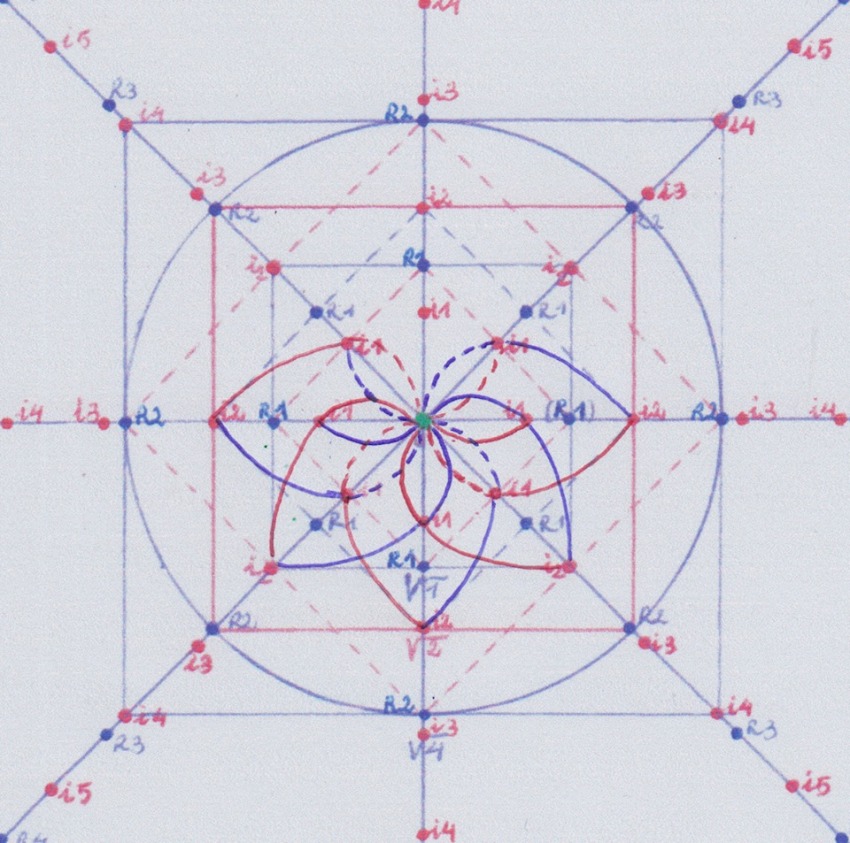
Pero al llegar al grado 5 encontramos de nuevo el problema:
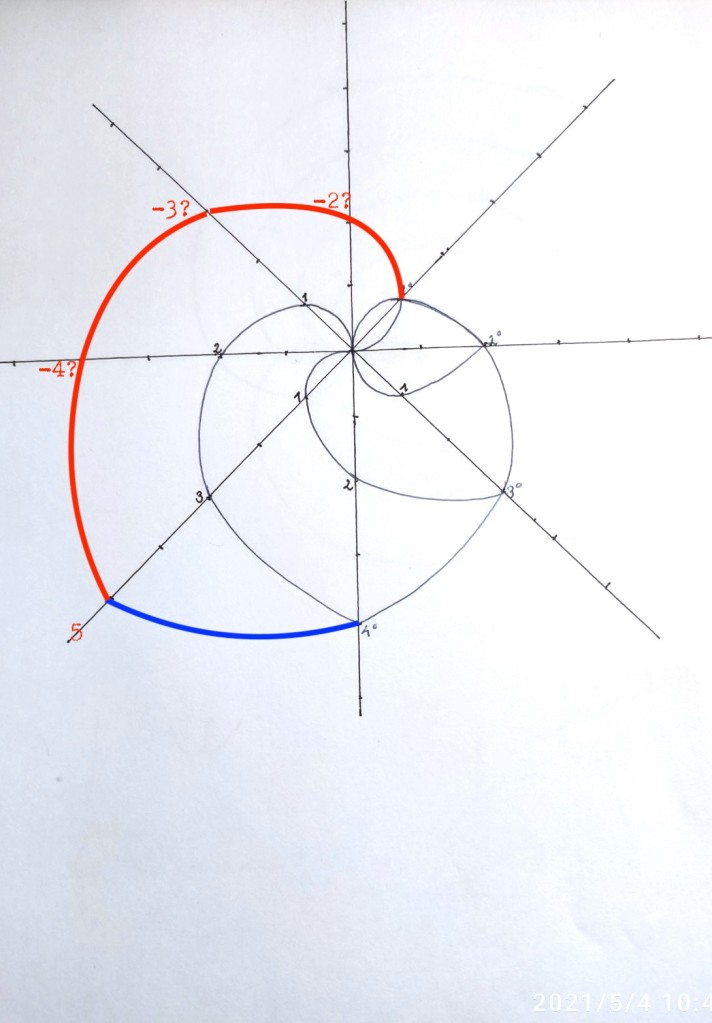
En este caso no se ha creado una nueva extensión de grado -1, sino que el cuerpo inicial de grado 1 se usa por la función de grado +5 y por su función opuesta de grado -5. Es decir, se vuelve al punto de partida, y la intersección de ambas funciones no se produce en el punto cero sino en el punto 1 de la coordenada Z.
Podemos pensar que el punto de intersección de las dos funciones, al ser idénticas aunque opuestas de signo, sería el punto = 0. Pero este punto se halla desplazado en la coordenada Z desde cero hasta uno.

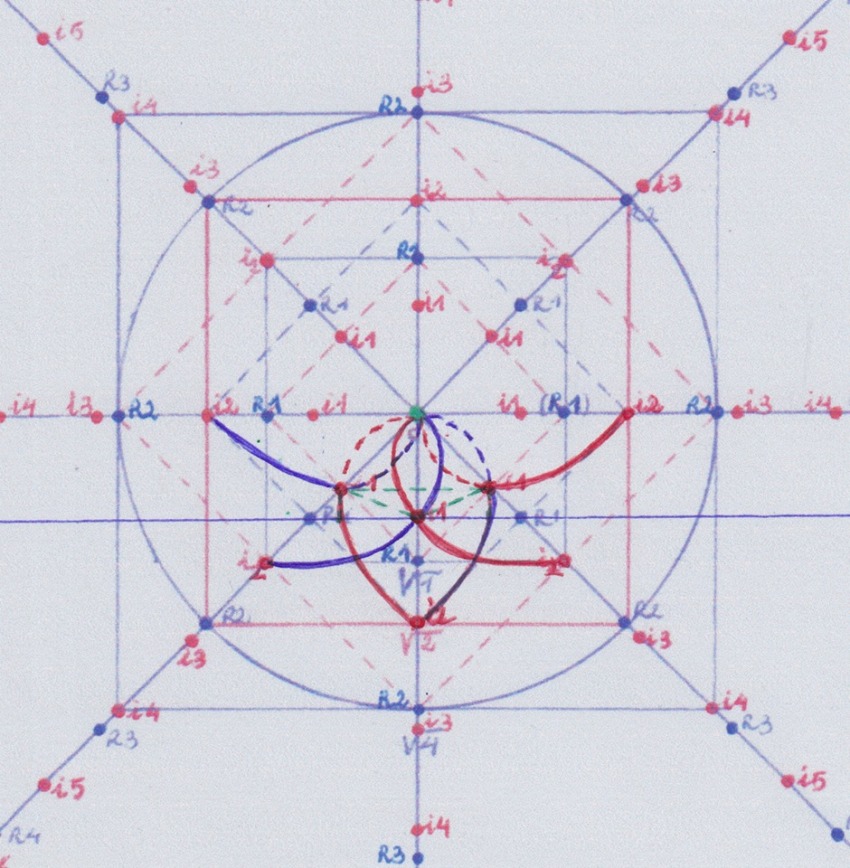
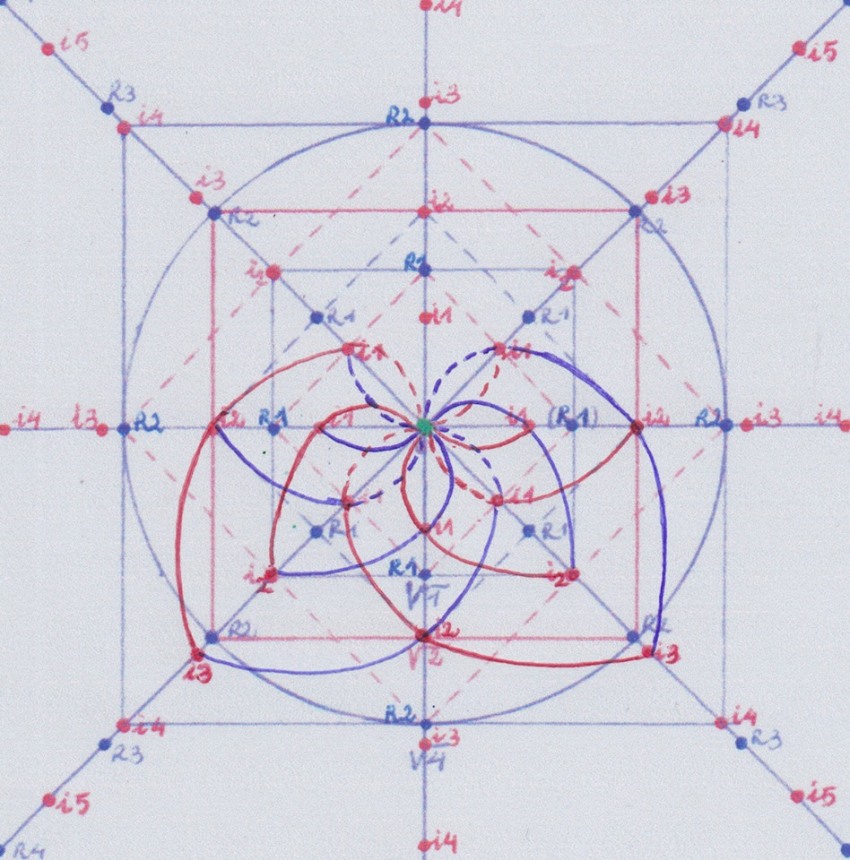
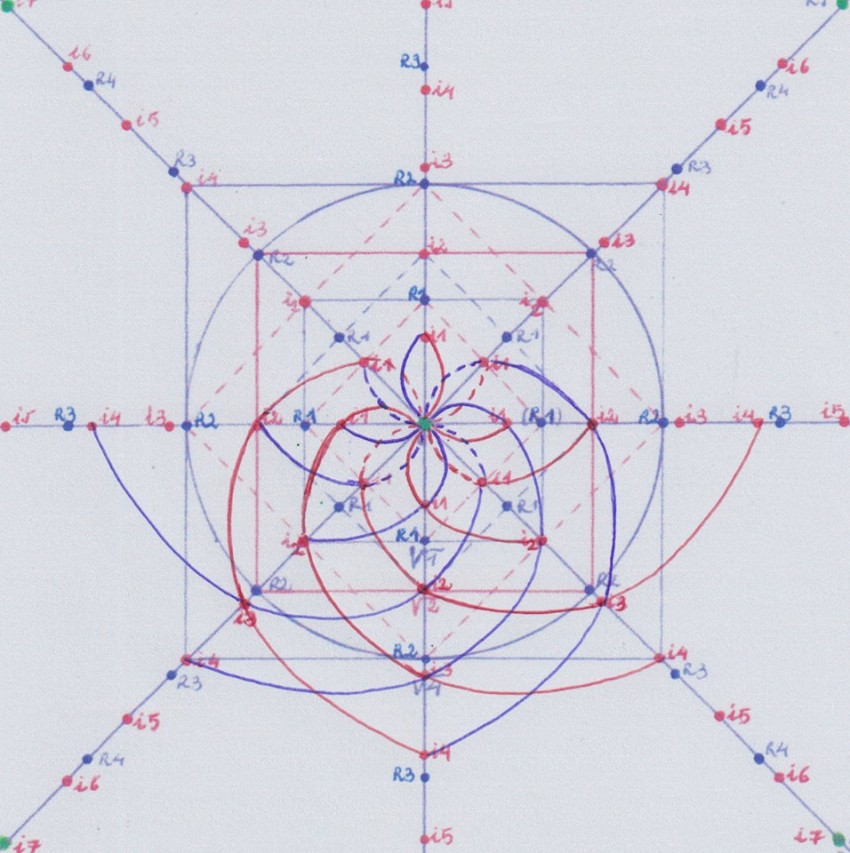
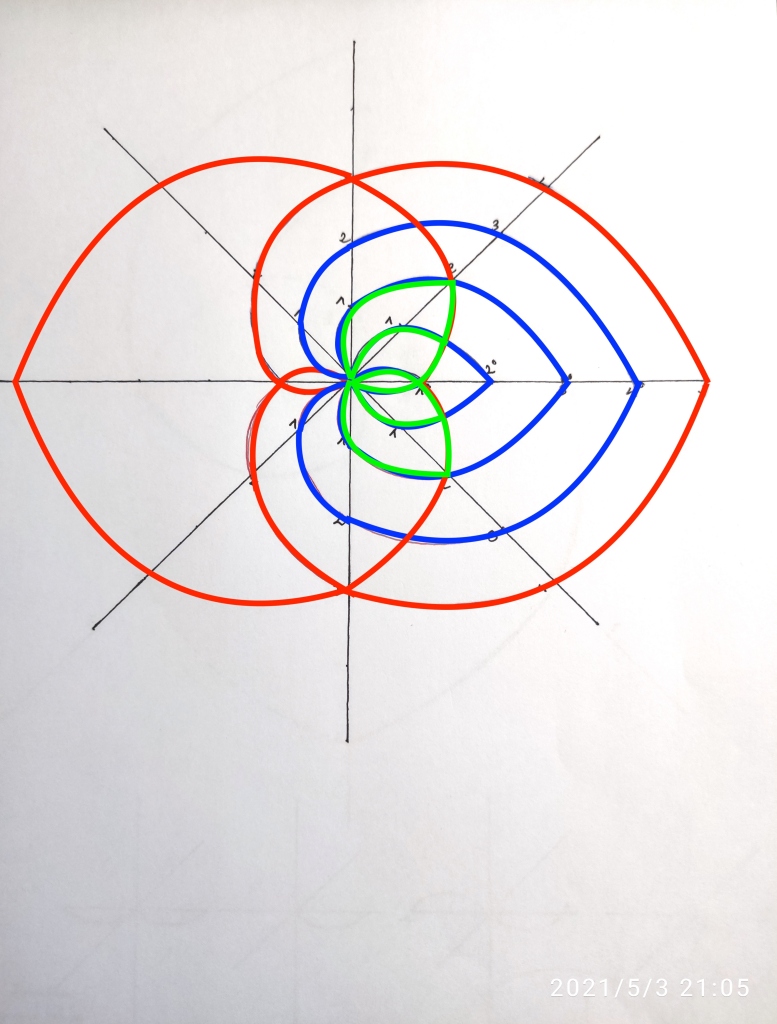
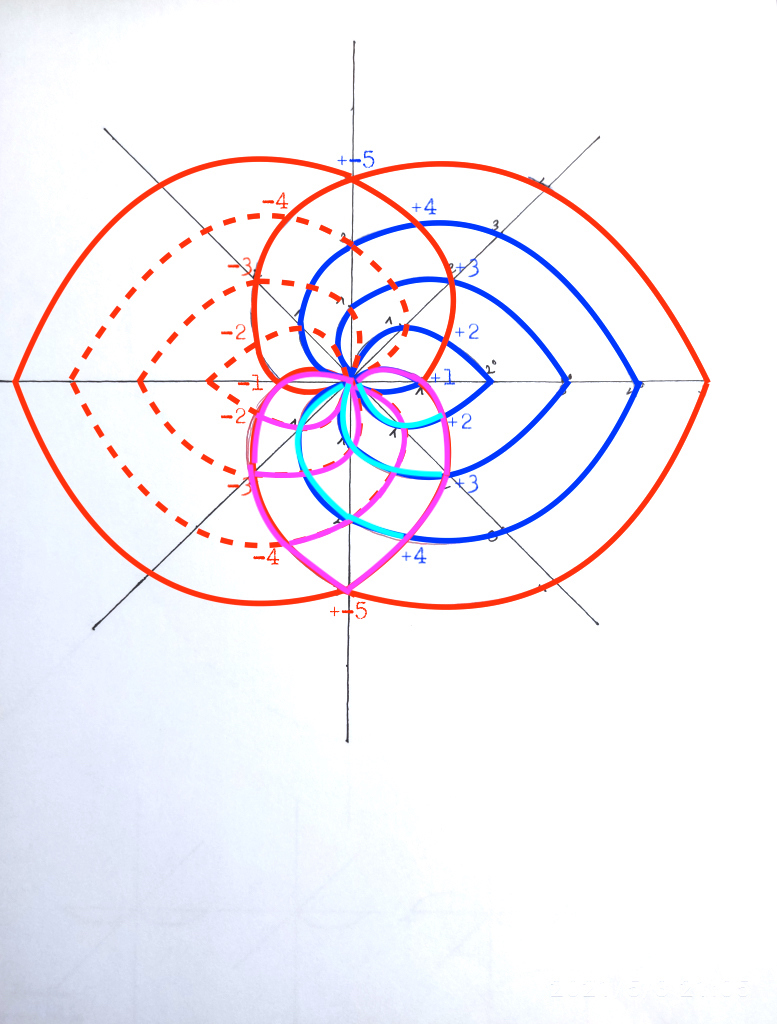
Si creamos la extensión inversa tenemos que:
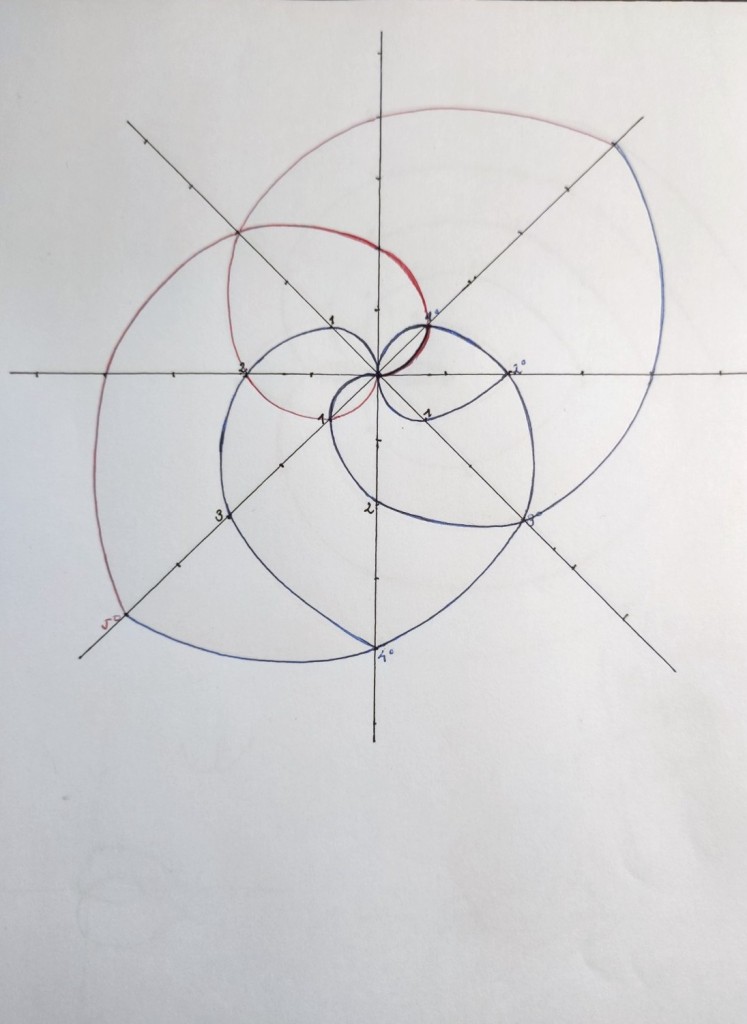
Pero aquí nos falta la extensión intermedia de grado 4 que nos sirva para pasar de la extensión 3 a la extensión 5.
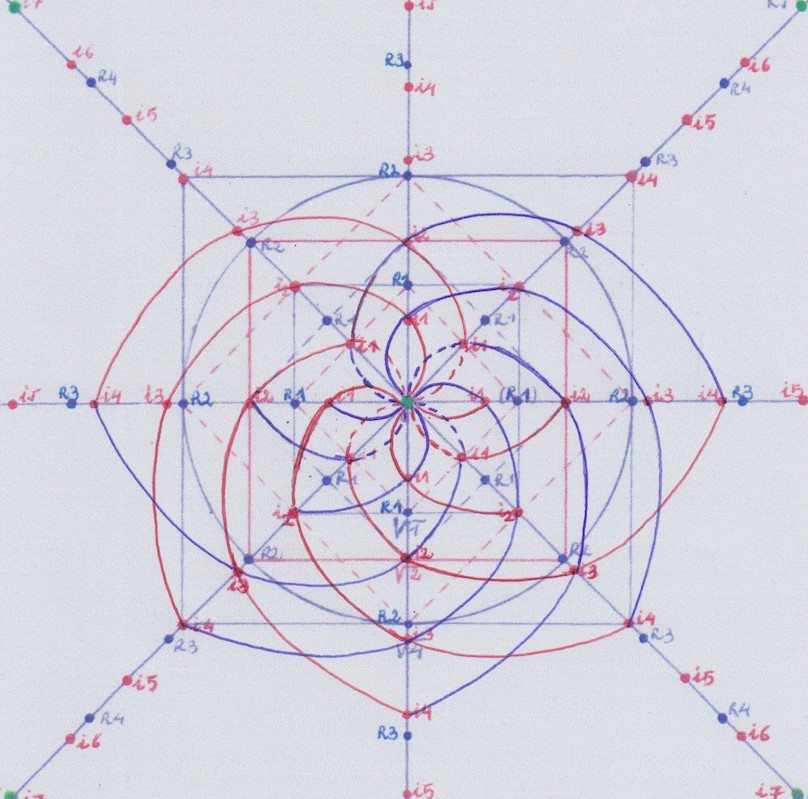
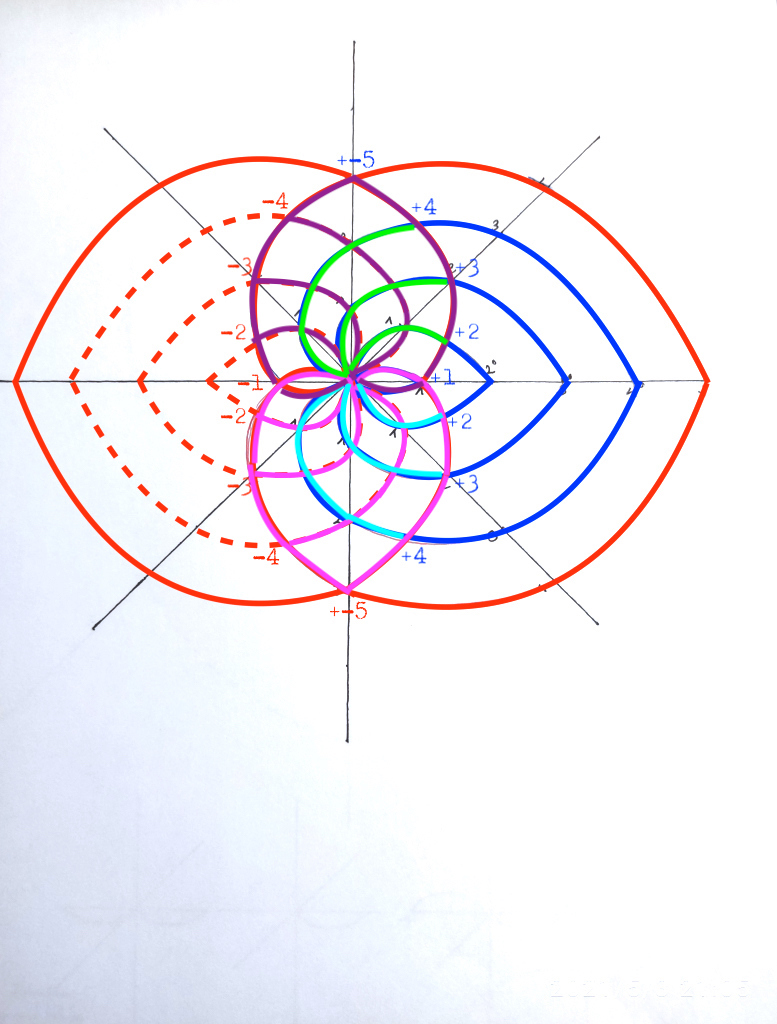
Para obtenerla, necesitamos prolongar una de las curvas de la extensión 2 hasta la instancia 4; y por otra parte necesitamos crear un nuevo cuerpo inicial de grado 1 y construir a partir de él las extensiones de grados 2 y 3:
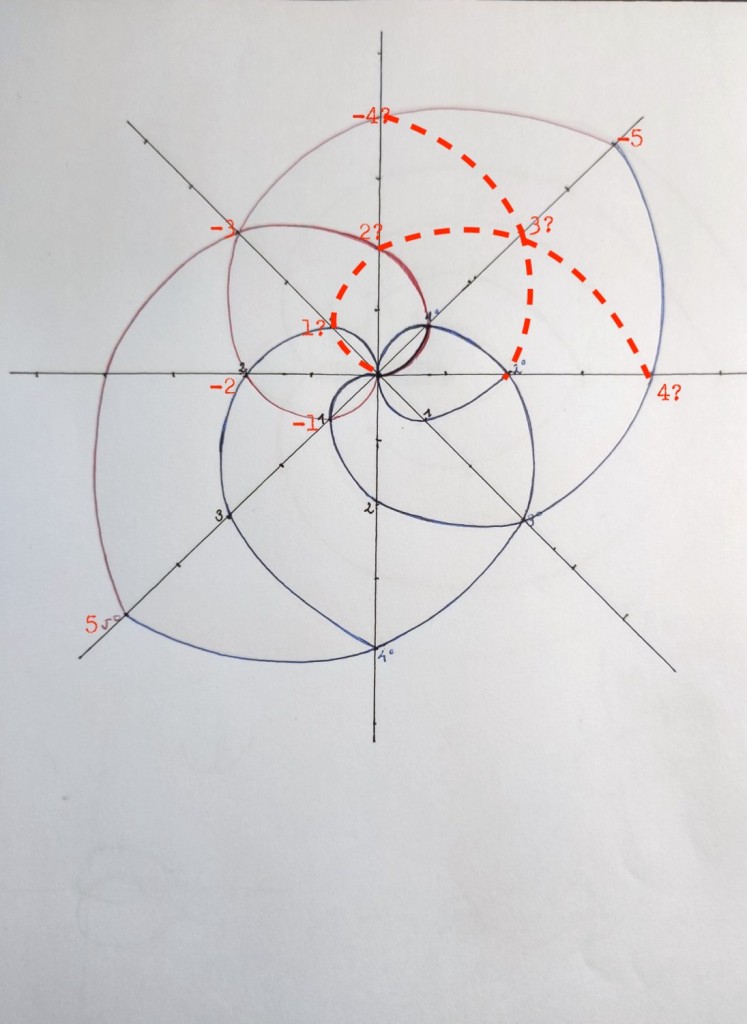
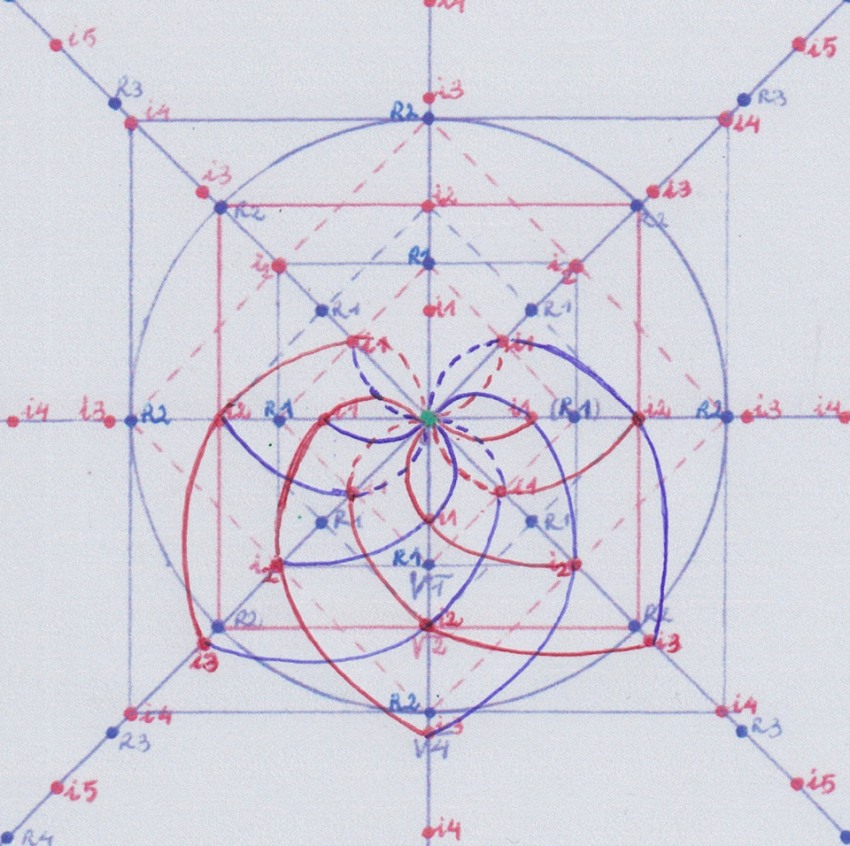
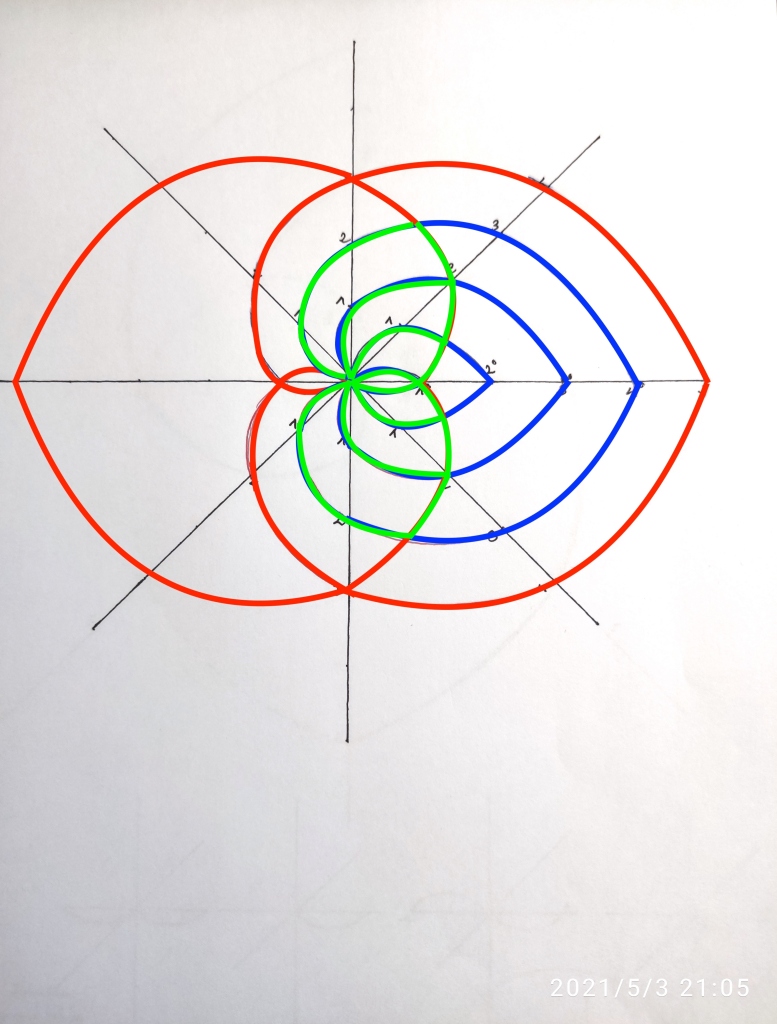
Y de forma similar haremos lo mismo en el lado inverso:
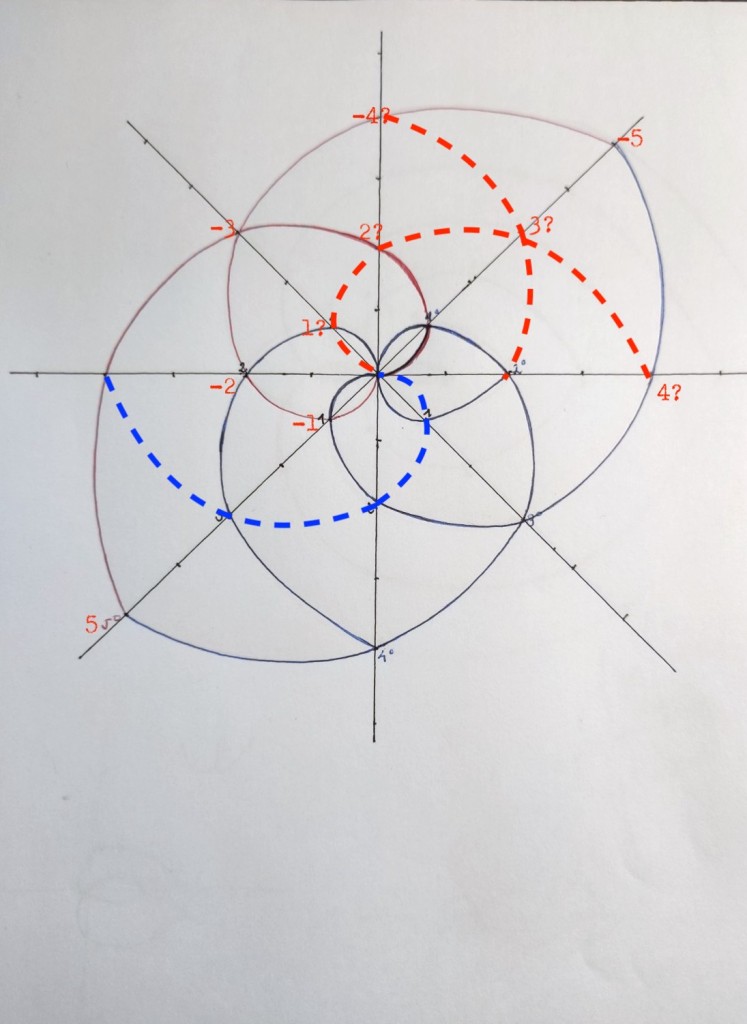
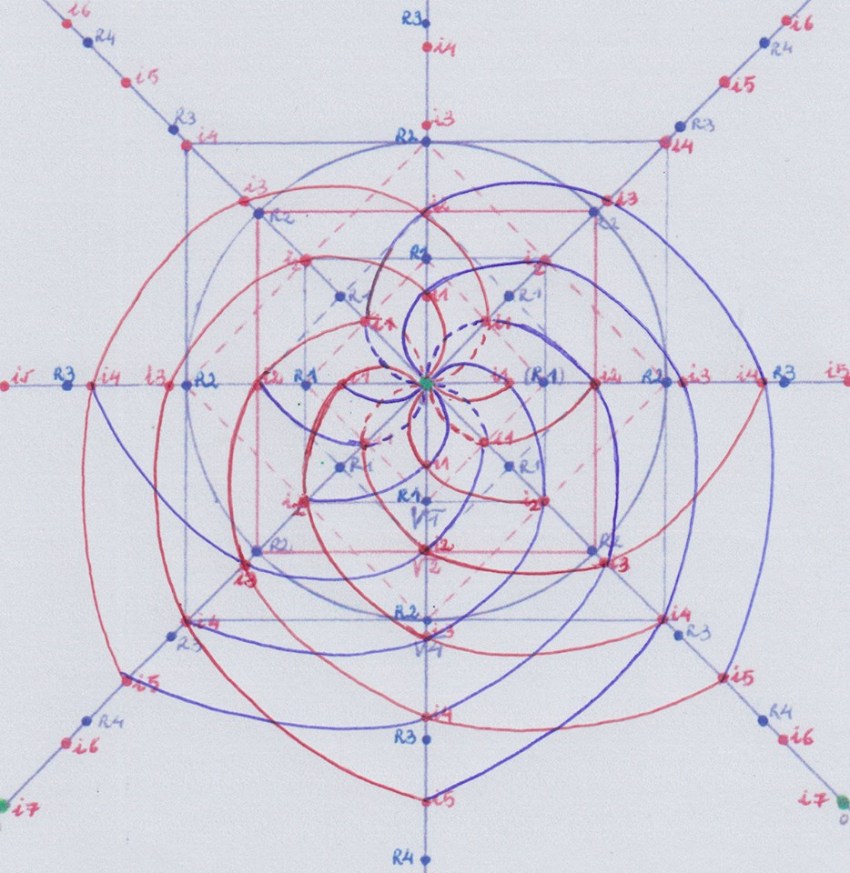
Hasta aquí hemos necesitado usar cuatro cuerpos iniciales de grado 1 para construir dos funciones simétricas de grado cinco. Pero tendríamos que las dos extensiones de grado 5 tienen su punto de intersección desplazado con respecto al de las de grado inferior.
En todo caso, el desarrollo de la simetría de estas estructuras conducirá al mismo resultado que hemos visto en las figuras anteriores.
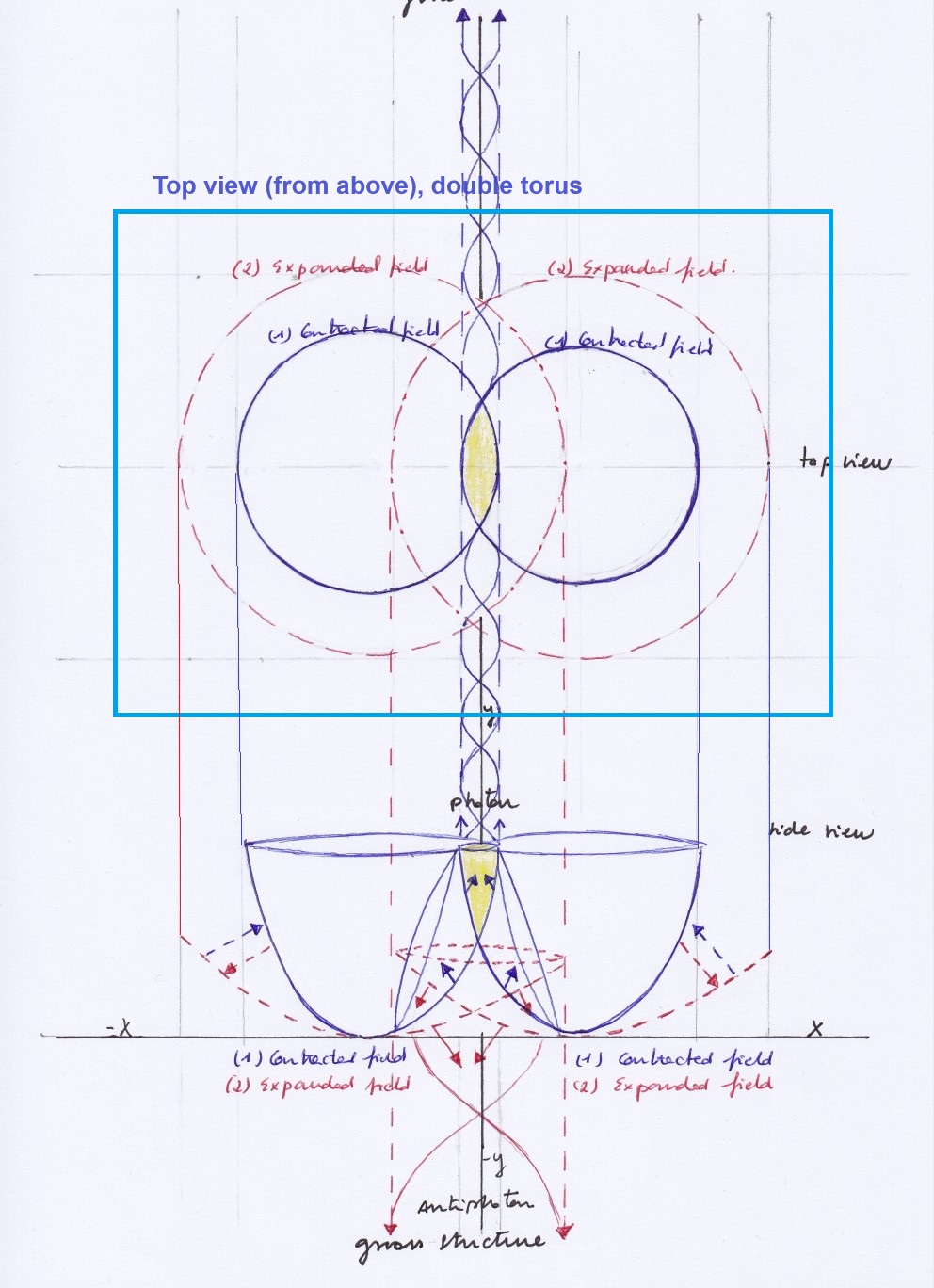
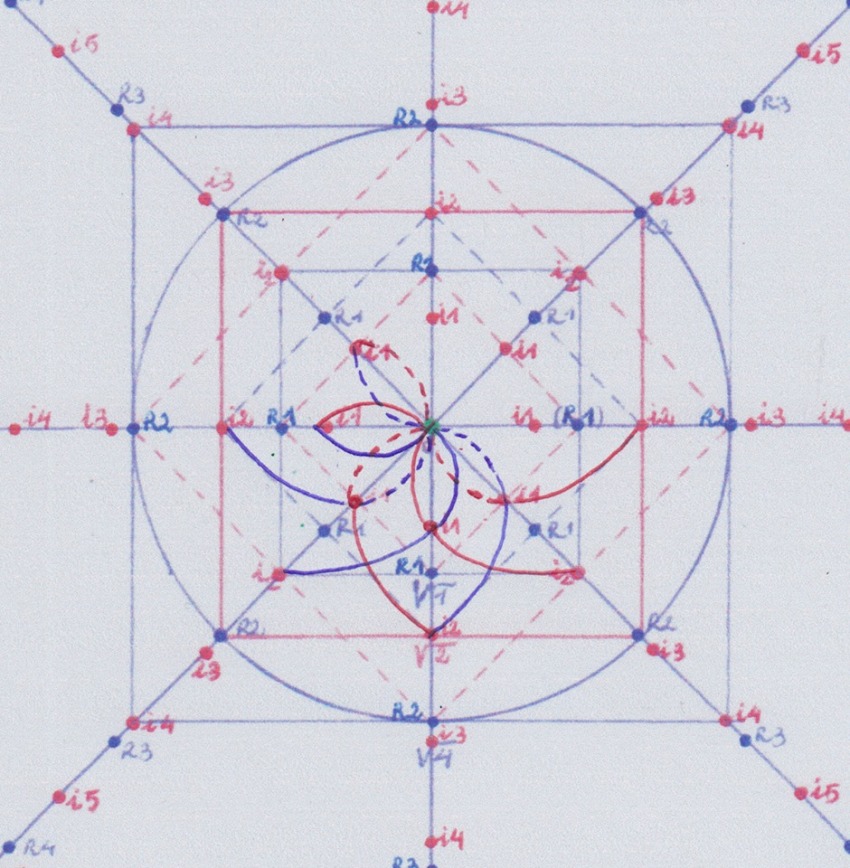
Pero, y si la permutación de la función inicial 1, en vez de hacerla en el plano horizontal la dirigimos hacia el plano ortogonal, no podemos construir así una extensión de grado 5 que no sea una doble extensión de la función 1? Y si podemos hacerlo, no mantendrá la extensión 5 ortogonal la simetría del grupo 1 a 4 horizontal?
Pienso que no, porque al estar usando ocho coordenadas para hacer las permutaciones, siempre se va a producir repetición del cuerpo 1 en la extensión de grado 5, ya que esta extensión formada por la intersección de las funciones +5 y – 5 requiere 10 permutaciones.
Un cordial saludo.



Escribe tu comentario