A principios del Siglo 19, Evariste Galois, un joven Escorpio de 20 años, dejó escrito la noche antes de batirse en un duelo mortal que las ecuaciones representan algebraicamente grupos de simetría y que esta simetría se rompe viniendo a ser mucho más compleja con las de quinto y superior grado; es por ello que estas ecuaciones no pueden resolverse con operaciones simples, como antes de morir de tuberculosis había ya demostrado hacía poco otro joven de 26 años, más pobre que una miserable rata, Neils Abel.
Todavía hubo que esperar tiempo, como pasa siempre, hasta que alguien entendiera lo que habían querido decir, pero así quedó finalmente resuelto un problema que había traido locos a los matemáticos desde la antigüedad, cuál es la fórmula general para resolver ecuaciones de 5 y mayor grado con simples operaciones de suma, resta, multiplicación… la respuesta fue que tal fórmula no existe.
Los trabajos de estos dos jóvenes dieron lugar a muchos desarrollos posteriores que cambiarían toda la matemática y la física que sostiene, dando lugar al nacimiento del álgebra abstracta, la matemática moderna, que ya no se pregunta por la resolución de ecuaciones sino por la estructura de los grupos y su simetría.
Ahora bien, lo que Galois no dejó dicho ni parece haber encontrado ningún matemático posterior es por qué la simetría se rompe en el quinto grado. Si lo hubieran sabido, probablemente se habrían dado cuenta de que el grupo de quinto grado existe, con la misma simple estructura de simetría que los anteriores, en unas coordenadas diferentes, es decir cuando el grupo se construye como una extensión rotada del grupo de 4 grado.
De manera que sin saber álgebra se puede razonablemente pensar que si la cusa de la imposibilidad de resolver las ecuaciones de 5 y superior grado era la creciente complejidad de la simetría, resuelto el problema de la simetría esas ecuaciones deberían poder resolverse de la misma forma que se resuelven las de grado inferior.
La ecuación que usan para resolverlas es Xˆ5 + Xˆ4 + Xˆ3 + Xˆ2 + X = 0, y esto lo simplifican a esta otra ecuación Xˆ5 – X – 1 = 0.
Pero pretender encontrar una fórmula general (es decir, hallar un valor para la X) de las ecuaciones quínticas partiendo de esta ecuación, es como querer encontrar todas las frutas buscando sólo en el cesto de las naranjas. A ver, en el cesto de las naranjas sólo hay naranjas. Si además queremos encontrar limones tendremos que buscar de otra manera. Así que no hay una fórmula general para las quínticas porque el polinomio que pregunta por ella no es general, es específico para un tipo específico de ecuaciones construidas sobre las referencias cuadráticas de XY.
El grupo de quinto grado que tiene la simetría simple que puede resolverse con radicales no está referenciado a XY sino a Z. Y en esa puñetera ecuación de los matemáticos no se pregunta por nada que esté en Z. Y si eliminan los polinomios de la ecuación operando de la forma en que lo hacen para simplificarla, pues menos aún. Porque Xˆ5 no se puede descomponer en Xˆ5, Xˆ4, Xˆ3, Xˆ2, X.
Xˆ5 se tiene que descomponer en en Xˆ5f(z), Xˆ4f(z), Xˆ3f(z), Xˆ2f(z), Xˆ1f(z) y para que eso pueda darse, tiene que poder construirse como una extensión desde Xˆ4 formada por Xˆ4f(xy), Xˆ3f(xy), Xˆ2f(xy), Xˆ1f(xy).
Esta sería una función cuártica – (coloreada en rojo), de 4 grado:
(Digo «Función» pero me refiero al campo (que tendría subcampos, con lo que sería un grupo) formado por la línea (formada por intervalos de puntos) que va por la derecha que sería su función +, y la línea que va por la izquierda que sería -. Las dos funciones tienen una simetria de espejo, y el campo estaría dividido en una parte positiva y una parte negativa, que tienen entre sí simetría de espejo, separadas por el eje Y. como el campo está por debajo del eje X, en su conjunto sería negativo.)
El problema que surge es que desde aquí no podemos crear un campo como hemos hecho con el campo anterior porque la línea derecha y la izquierda ya han convergido en el eje central Y en el punto 4, y ahora van hacia lados opuestos. Así que para construir el campo quíntico con una estructura similar tendríamos que retorcer esas líneas de manera que la figura resultante sería además de compleja completamente diferente. El campo quinto, con una estructura simple igual a la del campo cuarto, no existe ahí.
Pero sí podemos construir un campo de quinto grado si rotamos el eje Y y empezamos las dos líneas que forman el perímetro del campo en vez de desde el punto i0 desde el punto i1.
El punto i1 será el punto i0 para el nuevo campo rotado, y usando cuatro grados más (desde el punto de vista del campo rotado) podemos construir el campo de 5 grado con las dos líneas que convergerán en el eje z (el eje central de ese nuevo campo es el eje Z desde el punto de vista del campo de cuarto grado no rotado, pero será el eje Y desde el punto de vista del campo de quinto grado rotado.
De esta manera, visto desde el punto de referencia de las coordenadas XY del campo de cuarto grado, el campo de quinto grado rotado es un campo de 5 grados (formados por los intervalos i0-i1, i1-i2, i2-i3, i3-i4, i4-i5). Pero considerado desde las coordenadas del campo de quinto grado rotado, el campo de quinto grado está formado por sólo cuatro grados que serán los intervalos i1-i2, i2-i3, i3-i4, i4-i5.
Es esta la forma, en mi opinión de resolver el problema de la complejidad de la simetría en las funciones quínticas y de superior grado. Porque la extensión máxima para poder formar el campo siguiente son 4 grados (4 intervalos en las figuras), ya que más allá las dos funciones antisimétricas no convergen. (Podrán converger de en grados superiores pero ya se ha roto la continuidad).
Y lo mismo se puede decir de las funciones de grado superior a 5. Así para formar con la estructura de simetría cuadrangular un campo de grado 6, (lo que sería 4+2) tendremos que construirlo rotado empezando en vex de desde el punto cero o desde el punto 1, desde el punto 2. Así, usando sólo cuatro grados más sonseguimos la convergencia en el 6 grado.
De modo que para construir cualquier ecuación de grado 4+n, tenemos que construirla empezando desde el punto n. Y el campo 4+n quedará formado con la estructura de simetr;ia simple que puede resolverse con radicales (puesto que on radicales se puede resolver las estructuras de grado 4 e ingferior que tiene es esa misma simetría).
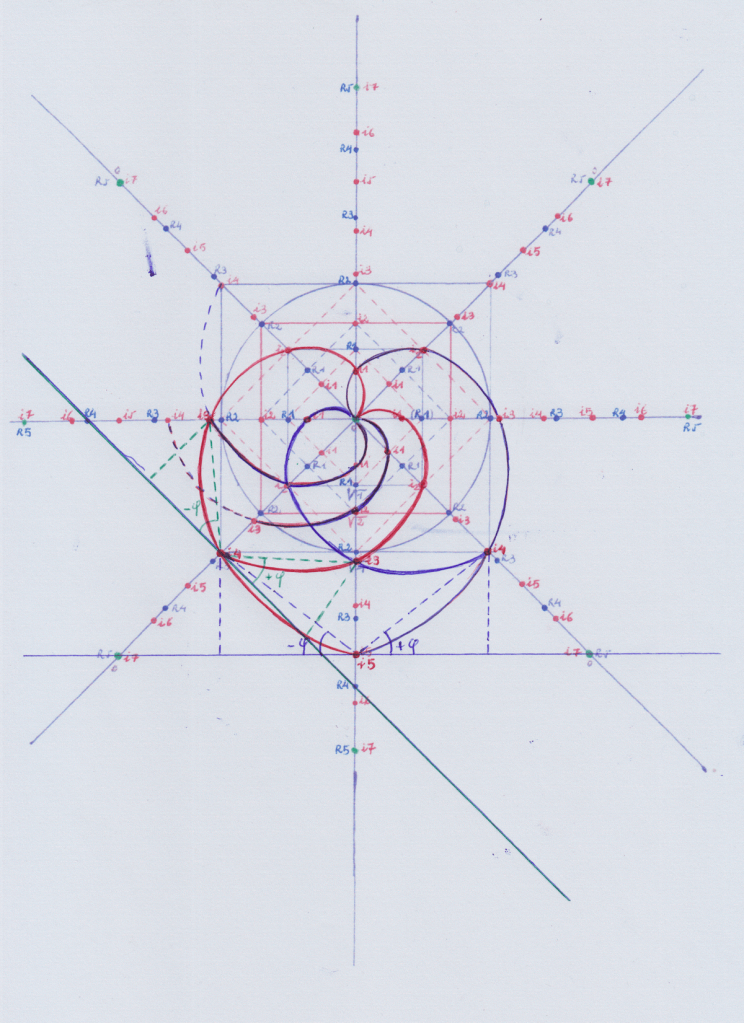
Esta sería una función quíntica + (coloreada en rojo y negro) rotada construída sobre Z:
Esta sería una de sexto grado (coloreada en verde)
Esat sería una función quíntica – (coloreada en rojo y negro)
Esta sería una función quártica + (invertida respecto a la primera) con el borde en negro:
Cuando trato de explicarles esto a los matemáticos lo primero que me dicen, cómo no, es que no entienden mi lenguage. Pero el problema en realidad no es que no entiendan este lenguaje sino que tampoco entienden esta geometría (ellos lo llaman «diagramas» que es como una forma de referirse a la geometría que no es algebraica, como si fuese un tipo de geometría menor que no se considera ya casi ni matemática). Porque la teoría de Galois, y toda la teoría de grupos, y prácticamente toda la matemática desde el Renacimiento, hasta la misma geometría, se ha desarrollado de forma exclusivamente algebraica. Y los matemáticos ( o una mayoría de ellos) no tienen una referencia visual para reconocer las simetrías de los grupos que ven en los signos de las ecuaciones representadas en una figura geométrica. No saben ni siquiera si estas representaciones geomérticas son o no grupos de Galois. Vamos, exactamente lo mismo que pasa con los físicos y el modelo atómico. Faltan las referencias materiales. Sólo están las ecuaciones.
Preguntad si no a cualquier matemático que os dibuje una aproximación visual de las simetrías de los grupos de Galois y de la asimetría de las ecuaciones de quinto grado.
No saben. Nadie se lo ha enseñado. Lo único que consiguen expresar fuera de las ecuaciones algebraicas son aproximaciones alegóricas o metafóricas. Por ejemplo, el caso de un edificio en el que entramos y vamos subiendo de planta por una escalera. Cada planta tiene su propia escalera que nos permite subir al piso siguiente. Pero cuando se llega al cuarto piso nos encontramos con que no hay escalera. Así que ni podemos ascender al quinto piso ni a los siguientes.
Respecto a esta analogía yo diría que no hay una sóla escalera sino dos, una derecha y otra izquierda (que tienen simetría de espejo), o dos lados de una escalinata, que convergen en el siguiente piso. Si las escaleras no convergen no es que no se pueda llegar de ninguna manera al quinto piso (las ecuaciones de quinto grado pueden resolverse con herramientas de cálculos más complejas) sino que el quinto piso se presenta como una estructura tan retorcida que es imposible acceder a ella sólo con nuestra escalera doble.
Pero a mi me parece que si se puede acceder al quinto piso con una simple escalera doble si hacemos una rotación de la escalera doble, porque el quinto piso que no está retorcido no está donde tenemos la escalera, tenemos que poner la escalera donde el quinto piso tiene la misma estructura que los pisos anteriores.
– – – – – – – – – – – – – – – – – – – – –
Este párrafo es nuevo, lo he añadido el 18 mayo:
He seguido pensando sobre este problema y creo que una forma más clara de representar la solución a la ruptura de la simetría de la función quíntica y superiores es darse cuenta de que el grupo de quinto grado que respetaría la simetría del grupo de 4 y menor grado sería un grupo formado a partir de dos grupos complejos «conjugados». (Entiendo que llaman «conjugados» a los grupos positivo y negativo que he representado más abajo, que tienen una simetría se espejo y una parte intersectada).
El grupo de quinto grado sería una extensión (cuando un campo menor está dentro de otro mayor se dice que el mayor es una extensión del meno) de dos grupo complejos conjugados.
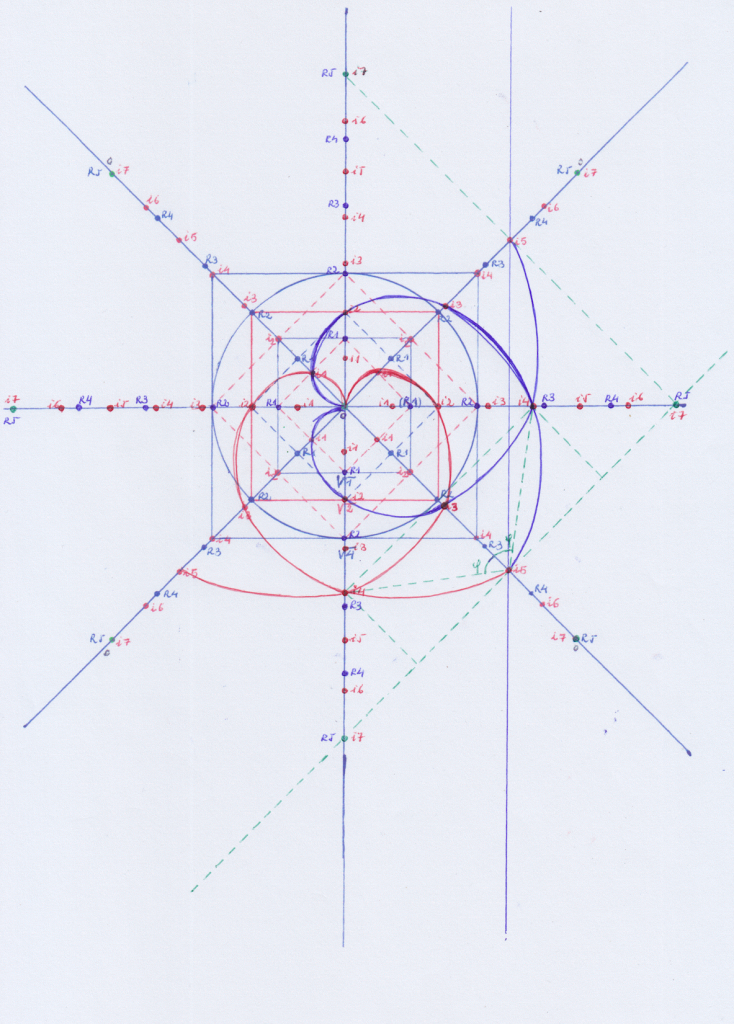
Así, si pensamos que esta figura única en rojo es un grupo de cuarto grado:
A partir de ella no podemos formar un grupo de quinto grado que tenga la misma simetría, porque las curvas ya convergieron en el punto del cuarto grado en la coordenada Y, y a partir de entonces divergen. Si quisiéramos que convergieran en el punto i5 (en la coordenada Y), tendríamos que cambiarlas de dirección y el resultado es una estructura que rompe con la simetría de los grupos de menor grado:
Sin embargo es posible construir un grupo de quinto grado a partir de dos grupos conjugados de cuarto grado (que a su vez estarán formados por dos grupos conjugados de tercer grado, etc), respectando la simetría.
Así el grupo de 5 grado puede construirse en Y, estando los dos grupos complejos conjugados de 4 grado en Z + y Z –
O también puede construirse este grupo simétrico de 5 grado sobre Z, estando los dos grupos conjugados de 5 grado en X y Y:
Entonces si según la teoría de Galois, la imposibilidad de resolver funciones quínticas (de quinto grado) es que en el grupo de quinto grado se rompe la simetría de manera que el grupo no puede resolverse con simples operaciones matemáticas, parece razonable pensar que una vez resuelto el problema de la simetría del grupo de quinto grado este debería de poder ser resuelto con radicales.
Habría que aclarar entonces si los grupos de quinto grado formados a partir de grupos complejos conjugados de 4 grado están siendo considerados o no por la Teoría de Galois al resolver funciones de quinto y mayor grado.
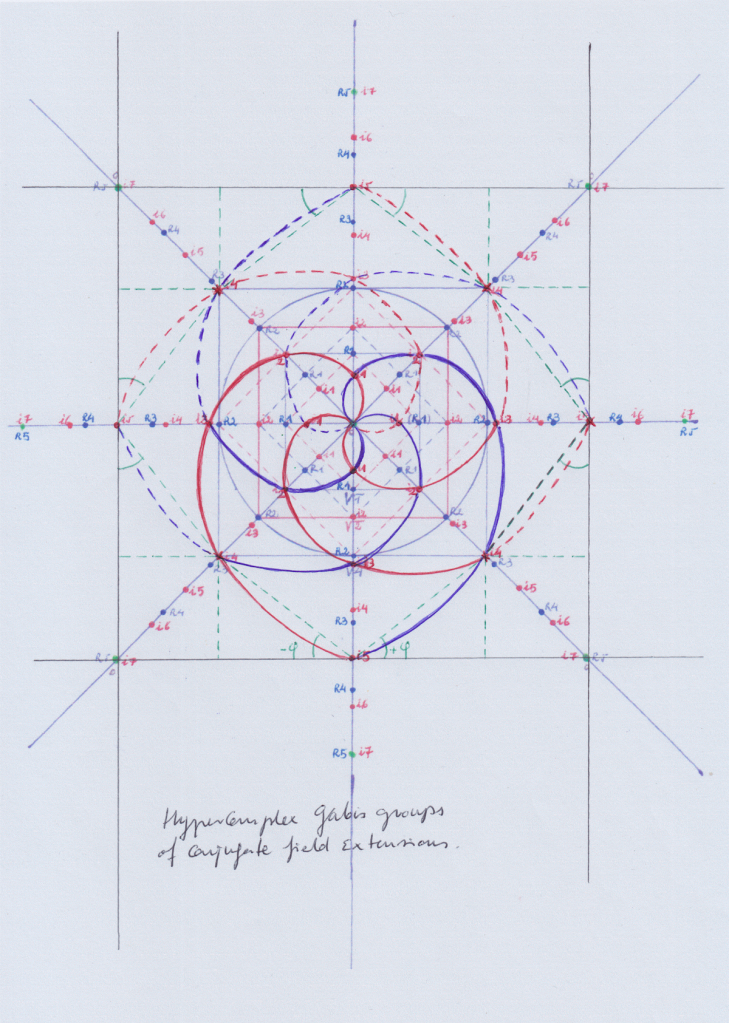
Si seguimos construyendo la figura podemos ver que todos los campos (o «cuerpos») siguen la misma estructura y todos respectan la misma simetría. En cada grado o nivel hay dos cuerpos conjugados que serían que serían un grupo de Galois y un campo (o «cuerpo») extendido de Galois. De manera que podemos formar grupos hipercomplejos de Galois formados por cuerpos hipercomplejos conjugados. Y las mismas extensions de los cuerpos serían extensiones complejas y conjugadas que darían lugar a nuevas extensiones.
Seguriré de todas maneras investigando y tratando de aclarar sin álgebra estos temas.
– – – – – – – – – – – – – – – – – – – – – –
Por otra parte, la idea de grupos de simetría de Galois surgió relacionada con el problema de las ecuaciones quínticas. Pero también fue usada después para demsotrar otro antiguo problema, el de si es o no posible dividor cualquier ángulo en tres partes iguales usando simplemente una regla y un compás que es lo que se conoce como la «trisección del ángulo».
El matemático farncés Pierre Wantzel demostró a mediados del Siglo XIX que no era posible tampoco encontrar una solución general al problema de la trisección. Se puede leer aquí: demostración.
Si para hacerlo utilizó los grupos de Galois, podemos pensar que si el problema de la simetría de Galois podemos resolverlo por medio de una extensión (supongo que es lo que llama «proyección» en geometría proyectiva), el problema de la simetría en el ángulo también podría resolverse del mismo modo. Pero si hacemos una extensión en el ángulo para restablecer una simetría con la que podamos trabajar de forma cuadrangular (referida a nuestras coordemadas XY, por ejemplo un ángulo de 90 grados), lo que hacemos es cambiar el ángulo mismo, lo que no tiene en este caso sentido.
Pero tal vez, sobre esto tengo todavía que pensar más, desde esa proyección en la que fácilmente podemos dividor el ángulo en tres, se pueda hacer una «contra-proyección» hacia el ángulo primitivo, puesto que las referencias de lo que sería la divisón ya las tenemos.
Este sería un ángulo en el que la simetría que tiene permite resolver la trisección sin problema:
Pero no pasaría lo mismo si en vez de en i4, i6, la base estuviera construída en i5 ,i6.
Yo me imagino que tiene que ver gente en matemáticas que esté avanzando en el desarrollo de lo que llaman «geometría visual» y que piense como yo que hay que poner coto a los desmanes que se han cometido con el álgebra en el desarrollo de las matemáticas de los cinco últimos siglos. La situación actual es tan delirante que los matemáticos construyen ecuaciones algebraicas que no saben a qué estructuras materiales corresponden y ni siquiera si es que tienen existencia material alguna. Y cuando les presentas visualmente una estructura de simetría no saben decirte a cual de sus entes algebraicos corresponde. Y si trats de explicárselo con palabras, porque la geometría que les presentas no la reconocen al no ser alegebarica, te piden que les definas los términos.
Es como si alguien que no ha visto nunca la Catedral de Santiago pero que tiene registradas las medidas de la fachada principal, se pusiera a describir con ecuaciones algebraicas el estilo románico del maestro Mateo. Y si tú, con afán de aprender, le preguntas qué son las figuras del arco más alto de la puerta central del Pórtico de la Gloria, te respondiera: «ESO NO ES LENGUAGE MATEMÁTICO ESTANDAR!!!»
(Nota> Los anuncios que pueden salir más abajo la pone la empresa propietaria de la plataforma del blog, ya que este es gratuito aunque la url no lo sea).
Actualización 14 septiembre 2021
También podemos ver el problema que surge en la resolución de las ecuaciones de quinto y superior grado a través del siguiente gráfico, en el que partimos de una función de grado 1 en la coordenada z, y la vamos rotando a través de las diferentes coordenadas X Y Z. Cada rotación o permutación representa un grado exponencial mayor.
Podemos resolver la función de grado 1 obteniendo un resultado igual a cero si oponemos una función inversa de grado 1, es decir, una función de grado -1. Al enfrentar ambas curvas opuestas además obtenemos un cuerpo delimitado por las dos curvas, que será de grado 1.
Pero cuando llegamos a la quinta permutación nos encontramos con que nos falta el primer tramo, el de grado 1 que nos permita trazar la curva inversa de grados 2, 3, 4 y 5 que se oponga a la curva de grados -1, -2, -3, -4, -5.
A principios del Siglo 19, Evariste Galois, un joven Escorpio de 20 años, dejó escrito la noche antes de batirse en un duelo mortal que las ecuaciones representan algebraicamente grupos de simetría y que esta simetría se rompe viniendo a ser mucho más compleja con las de quinto y superior grado; es por ello que estas ecuaciones no pueden resolverse con operaciones simples, como antes de morir de tuberculosis había ya demostrado hacía poco otro joven de 26 años, más pobre que una miserable rata, Neils Abel.
Todavía hubo que esperar tiempo, como pasa siempre, hasta que alguien entendiera lo que habían querido decir, pero así quedó finalmente resuelto un problema que había traido locos a los matemáticos desde la antigüedad, cuál es la fórmula general para resolver ecuaciones de 5 y mayor grado con simples operaciones de suma, resta, multiplicación… la respuesta fue que tal fórmula no existe.
Los trabajos de estos dos jóvenes dieron lugar a muchos desarrollos posteriores que cambiarían toda la matemática y la física que sostiene, dando lugar al nacimiento del álgebra abstracta, la matemática moderna, que ya no se pregunta por la resolución de ecuaciones sino por la estructura de los grupos y su simetría.
Ahora bien, lo que Galois no dejó dicho ni parece haber encontrado ningún matemático posterior es por qué la simetría se rompe en el quinto grado. Si lo hubieran sabido, probablemente se habrían dado cuenta de que el grupo de quinto grado existe, con la misma simple estructura de simetría que los anteriores, en unas coordenadas diferentes, es decir cuando el grupo se construye como una extensión rotada del grupo de 4 grado.
De manera que sin saber álgebra se puede razonablemente pensar que si la cusa de la imposibilidad de resolver las ecuaciones de 5 y superior grado era la creciente complejidad de la simetría, resuelto el problema de la simetría esas ecuaciones deberían poder resolverse de la misma forma que se resuelven las de grado inferior.
La ecuación que usan para resolverlas es Xˆ5 + Xˆ4 + Xˆ3 + Xˆ2 + X = 0, y esto lo simplifican a esta otra ecuación Xˆ5 – X – 1 = 0.
Pero pretender encontrar una fórmula general (es decir, hallar un valor para la X) de las ecuaciones quínticas partiendo de esta ecuación, es como querer encontrar todas las frutas buscando sólo en el cesto de las naranjas. A ver, en el cesto de las naranjas sólo hay naranjas. Si además queremos encontrar limones tendremos que buscar de otra manera. Así que no hay una fórmula general para las quínticas porque el polinomio que pregunta por ella no es general, es específico para un tipo específico de ecuaciones construidas sobre las referencias cuadráticas de XY.
El grupo de quinto grado que tiene la simetría simple que puede resolverse con radicales no está referenciado a XY sino a Z. Y en esa puñetera ecuación de los matemáticos no se pregunta por nada que esté en Z. Y si eliminan los polinomios de la ecuación operando de la forma en que lo hacen para simplificarla, pues menos aún. Porque Xˆ5 no se puede descomponer en Xˆ5, Xˆ4, Xˆ3, Xˆ2, X.
Xˆ5 se tiene que descomponer en en Xˆ5f(z), Xˆ4f(z), Xˆ3f(z), Xˆ2f(z), Xˆ1f(z) y para que eso pueda darse, tiene que poder construirse como una extensión desde Xˆ4 formada por Xˆ4f(xy), Xˆ3f(xy), Xˆ2f(xy), Xˆ1f(xy).
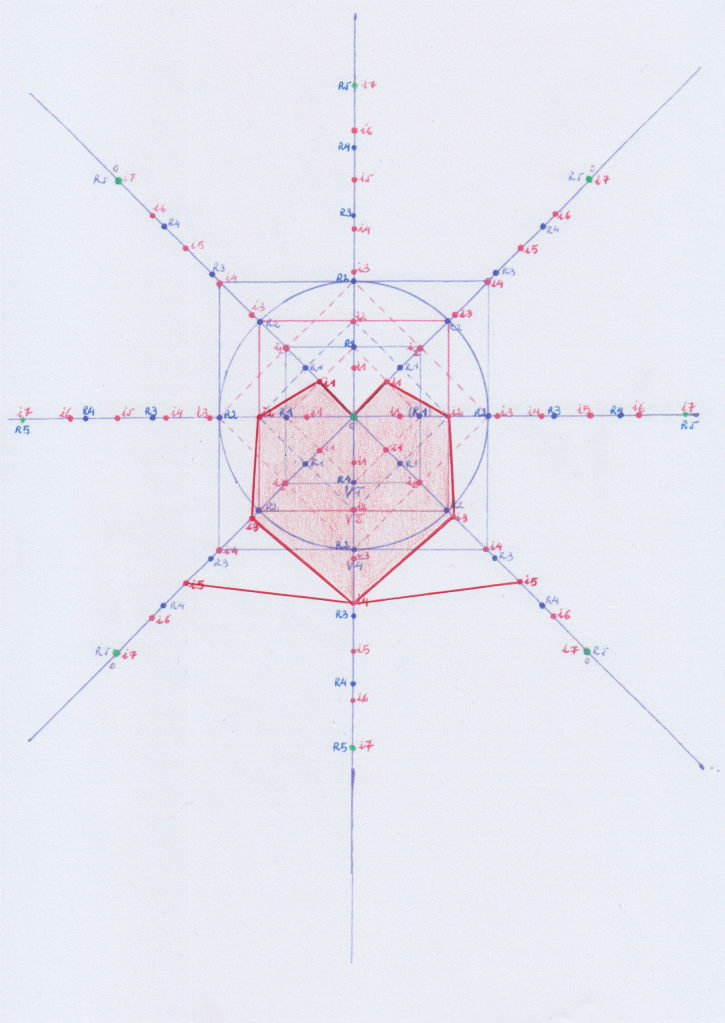
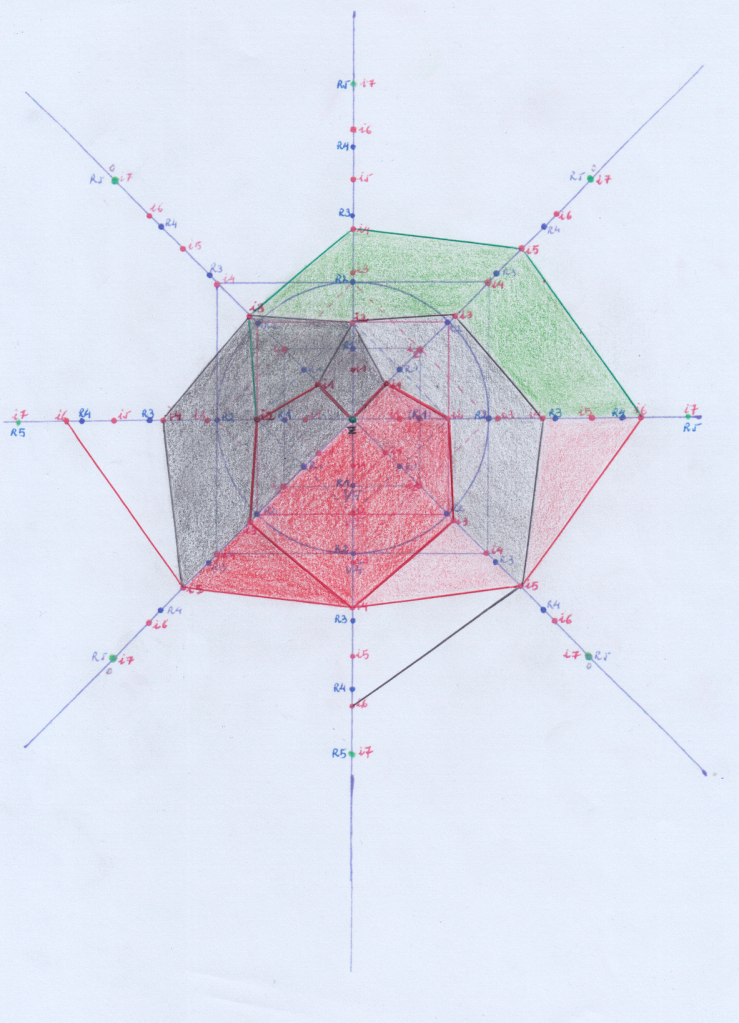
Esta sería una función cuártica – (coloreada en rojo), de 4 grado:
(Digo «Función» pero me refiero al campo (que tendría subcampos, con lo que sería un grupo) formado por la línea (formada por intervalos de puntos) que va por la derecha que sería su función +, y la línea que va por la izquierda que sería -. Las dos funciones tienen una simetria de espejo, y el campo estaría dividido en una parte positiva y una parte negativa, que tienen entre sí simetría de espejo, separadas por el eje Y. como el campo está por debajo del eje X, en su conjunto sería negativo.)
El problema que surge es que desde aquí no podemos crear un campo como hemos hecho con el campo anterior porque la línea derecha y la izquierda ya han convergido en el eje central Y en el punto 4, y ahora van hacia lados opuestos. Así que para construir el campo quíntico con una estructura similar tendríamos que retorcer esas líneas de manera que la figura resultante sería además de compleja completamente diferente. El campo quinto, con una estructura simple igual a la del campo cuarto, no existe ahí.
Pero sí podemos construir un campo de quinto grado si rotamos el eje Y y empezamos las dos líneas que forman el perímetro del campo en vez de desde el punto i0 desde el punto i1.
El punto i1 será el punto i0 para el nuevo campo rotado, y usando cuatro grados más (desde el punto de vista del campo rotado) podemos construir el campo de 5 grado con las dos líneas que convergerán en el eje z (el eje central de ese nuevo campo es el eje Z desde el punto de vista del campo de cuarto grado no rotado, pero será el eje Y desde el punto de vista del campo de quinto grado rotado.
De esta manera, visto desde el punto de referencia de las coordenadas XY del campo de cuarto grado, el campo de quinto grado rotado es un campo de 5 grados (formados por los intervalos i0-i1, i1-i2, i2-i3, i3-i4, i4-i5). Pero considerado desde las coordenadas del campo de quinto grado rotado, el campo de quinto grado está formado por sólo cuatro grados que serán los intervalos i1-i2, i2-i3, i3-i4, i4-i5.
Es esta la forma, en mi opinión de resolver el problema de la complejidad de la simetría en las funciones quínticas y de superior grado. Porque la extensión máxima para poder formar el campo siguiente son 4 grados (4 intervalos en las figuras), ya que más allá las dos funciones antisimétricas no convergen. (Podrán converger de en grados superiores pero ya se ha roto la continuidad).
Y lo mismo se puede decir de las funciones de grado superior a 5. Así para formar con la estructura de simetría cuadrangular un campo de grado 6, (lo que sería 4+2) tendremos que construirlo rotado empezando en vex de desde el punto cero o desde el punto 1, desde el punto 2. Así, usando sólo cuatro grados más sonseguimos la convergencia en el 6 grado.
De modo que para construir cualquier ecuación de grado 4+n, tenemos que construirla empezando desde el punto n. Y el campo 4+n quedará formado con la estructura de simetr;ia simple que puede resolverse con radicales (puesto que on radicales se puede resolver las estructuras de grado 4 e ingferior que tiene es esa misma simetría).
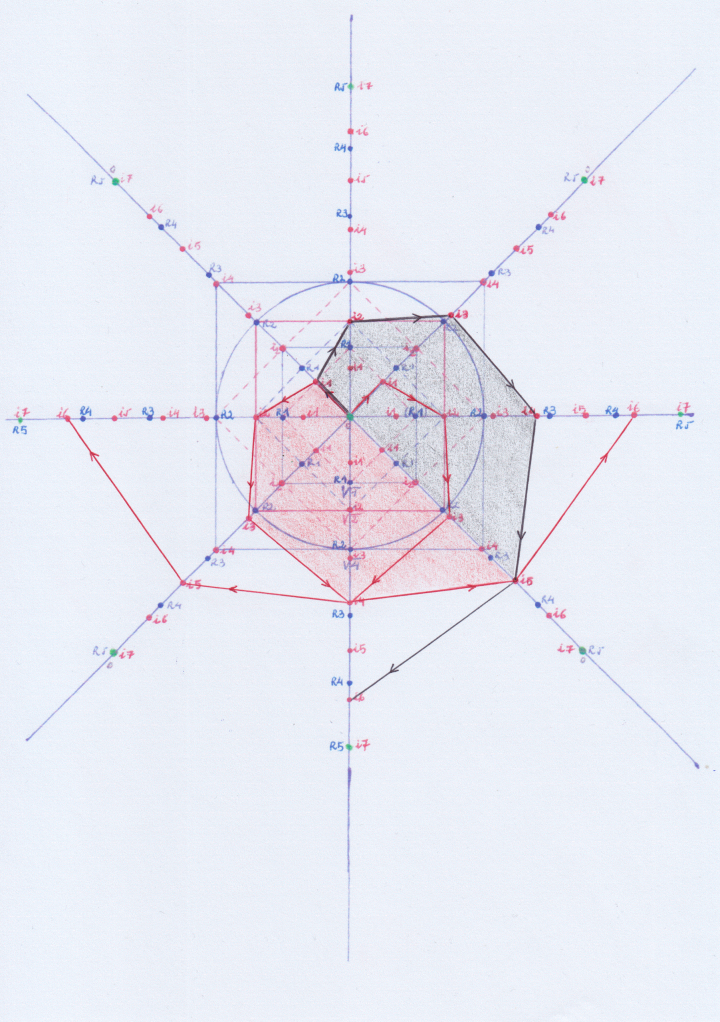
Esta sería una función quíntica + (coloreada en rojo y negro) rotada construída sobre Z:
Esta sería una de sexto grado (coloreada en verde)
Esat sería una función quíntica – (coloreada en rojo y negro)
Esta sería una función quártica + (invertida respecto a la primera) con el borde en negro:
Cuando trato de explicarles esto a los matemáticos lo primero que me dicen, cómo no, es que no entienden mi lenguage. Pero el problema en realidad no es que no entiendan este lenguaje sino que tampoco entienden esta geometría (ellos lo llaman «diagramas» que es como una forma de referirse a la geometría que no es algebraica, como si fuese un tipo de geometría menor que no se considera ya casi ni matemática). Porque la teoría de Galois, y toda la teoría de grupos, y prácticamente toda la matemática desde el Renacimiento, hasta la misma geometría, se ha desarrollado de forma exclusivamente algebraica. Y los matemáticos ( o una mayoría de ellos) no tienen una referencia visual para reconocer las simetrías de los grupos que ven en los signos de las ecuaciones representadas en una figura geométrica. No saben ni siquiera si estas representaciones geomérticas son o no grupos de Galois. Vamos, exactamente lo mismo que pasa con los físicos y el modelo atómico. Faltan las referencias materiales. Sólo están las ecuaciones.
Preguntad si no a cualquier matemático que os dibuje una aproximación visual de las simetrías de los grupos de Galois y de la asimetría de las ecuaciones de quinto grado.
No saben. Nadie se lo ha enseñado. Lo único que consiguen expresar fuera de las ecuaciones algebraicas son aproximaciones alegóricas o metafóricas. Por ejemplo, el caso de un edificio en el que entramos y vamos subiendo de planta por una escalera. Cada planta tiene su propia escalera que nos permite subir al piso siguiente. Pero cuando se llega al cuarto piso nos encontramos con que no hay escalera. Así que ni podemos ascender al quinto piso ni a los siguientes.
Respecto a esta analogía yo diría que no hay una sóla escalera sino dos, una derecha y otra izquierda (que tienen simetría de espejo), o dos lados de una escalinata, que convergen en el siguiente piso. Si las escaleras no convergen no es que no se pueda llegar de ninguna manera al quinto piso (las ecuaciones de quinto grado pueden resolverse con herramientas de cálculos más complejas) sino que el quinto piso se presenta como una estructura tan retorcida que es imposible acceder a ella sólo con nuestra escalera doble.
Pero a mi me parece que si se puede acceder al quinto piso con una simple escalera doble si hacemos una rotación de la escalera doble, porque el quinto piso que no está retorcido no está donde tenemos la escalera, tenemos que poner la escalera donde el quinto piso tiene la misma estructura que los pisos anteriores.
– – – – – – – – – – – – – – – – – – – – –
Este párrafo es nuevo, lo he añadido el 18 mayo:
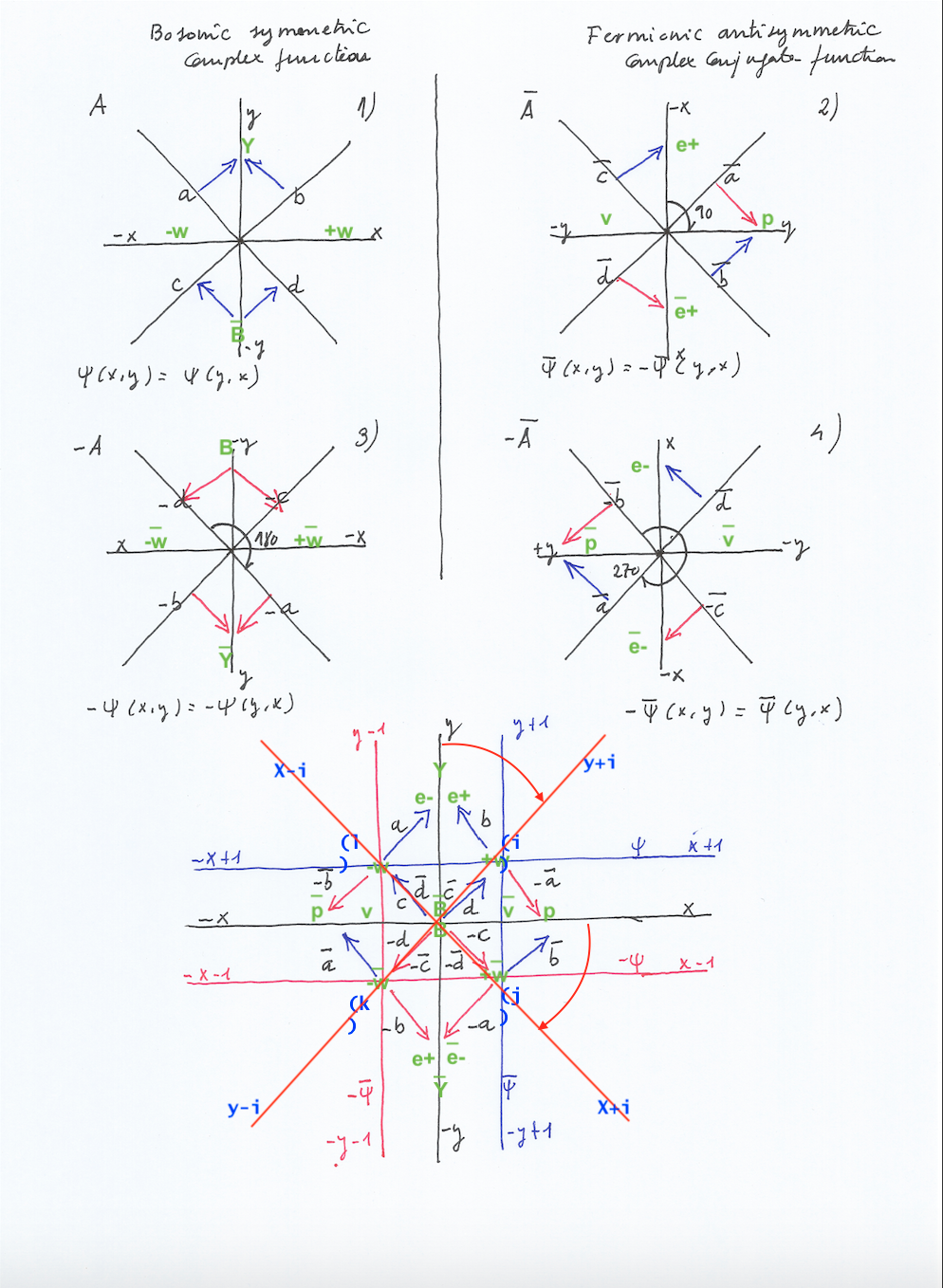
He seguido pensando sobre este problema y creo que una forma más clara de representar la solución a la ruptura de la simetría de la función quíntica y superiores es darse cuenta de que el grupo de quinto grado que respetaría la simetría del grupo de 4 y menor grado sería un grupo formado a partir de dos grupos complejos «conjugados». (Entiendo que llaman «conjugados» a los grupos positivo y negativo que he representado más abajo, que tienen una simetría se espejo y una parte intersectada).
El grupo de quinto grado sería una extensión (cuando un campo menor está dentro de otro mayor se dice que el mayor es una extensión del meno) de dos grupo complejos conjugados.
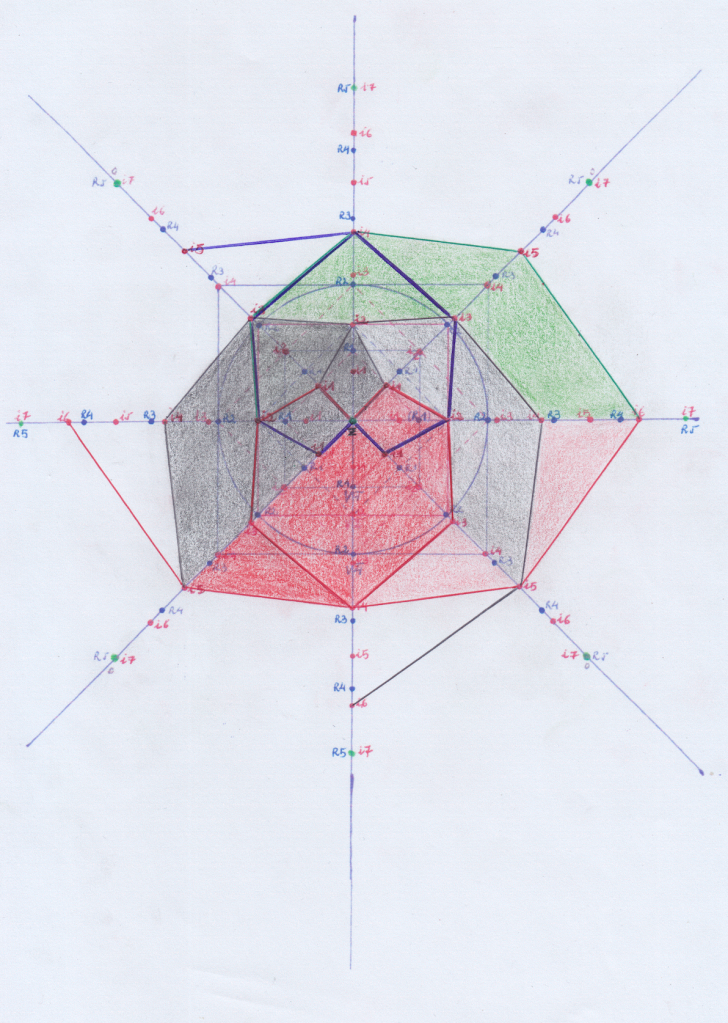
Así, si pensamos que esta figura única en rojo es un grupo de cuarto grado:
A partir de ella no podemos formar un grupo de quinto grado que tenga la misma simetría, porque las curvas ya convergieron en el punto del cuarto grado en la coordenada Y, y a partir de entonces divergen. Si quisiéramos que convergieran en el punto i5 (en la coordenada Y), tendríamos que cambiarlas de dirección y el resultado es una estructura que rompe con la simetría de los grupos de menor grado:
Sin embargo es posible construir un grupo de quinto grado a partir de dos grupos conjugados de cuarto grado (que a su vez estarán formados por dos grupos conjugados de tercer grado, etc), respectando la simetría.
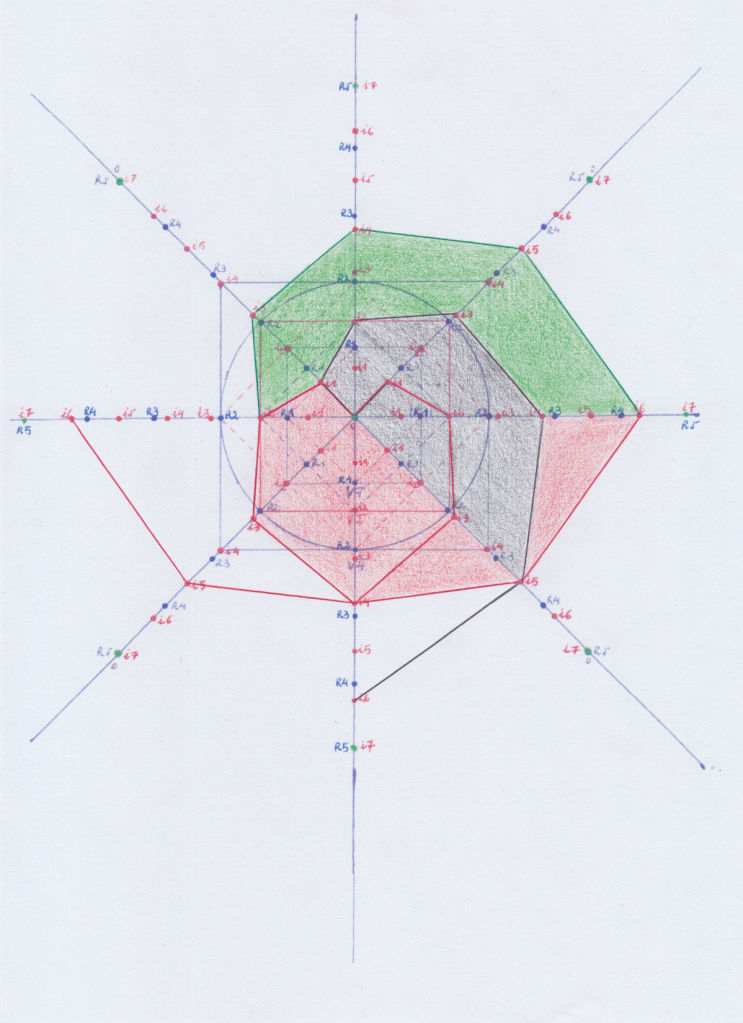
Así el grupo de 5 grado puede construirse en Y, estando los dos grupos complejos conjugados de 4 grado en Z + y Z –
O también puede construirse este grupo simétrico de 5 grado sobre Z, estando los dos grupos conjugados de 5 grado en X y Y:
Entonces si según la teoría de Galois, la imposibilidad de resolver funciones quínticas (de quinto grado) es que en el grupo de quinto grado se rompe la simetría de manera que el grupo no puede resolverse con simples operaciones matemáticas, parece razonable pensar que una vez resuelto el problema de la simetría del grupo de quinto grado este debería de poder ser resuelto con radicales.
Habría que aclarar entonces si los grupos de quinto grado formados a partir de grupos complejos conjugados de 4 grado están siendo considerados o no por la Teoría de Galois al resolver funciones de quinto y mayor grado.
Si seguimos construyendo la figura podemos ver que todos los campos (o «cuerpos») siguen la misma estructura y todos respectan la misma simetría. En cada grado o nivel hay dos cuerpos conjugados que serían que serían un grupo de Galois y un campo (o «cuerpo») extendido de Galois. De manera que podemos formar grupos hipercomplejos de Galois formados por cuerpos hipercomplejos conjugados. Y las mismas extensions de los cuerpos serían extensiones complejas y conjugadas que darían lugar a nuevas extensiones.
Seguiré de todas maneras investigando y tratando de aclarar sin álgebra estos temas.
– – – – – – – – – – – – – – – – – – – – – –
Por otra parte, la idea de grupos de simetría de Galois surgió relacionada con el problema de las ecuaciones quínticas. Pero también fue usada después para demostrar otro antiguo problema, el de si es o no posible dividir cualquier ángulo en tres partes iguales usando simplemente una regla y un compás que es lo que se conoce como la «trisección del ángulo».
El matemático francés Pierre Wantzel demostró a mediados del Siglo XIX que no era posible tampoco encontrar una solución general al problema de la trisección. Se puede leer aquí: demostración.
Si para hacerlo utilizó los grupos de Galois, podemos pensar que si el problema de la simetría de Galois podemos resolverlo por medio de una extensión (supongo que es lo que llama «proyección» en geometría proyectiva), el problema de la simetría en el ángulo también podría resolverse del mismo modo. Pero si hacemos una extensión en el ángulo para restablecer una simetría con la que podamos trabajar de forma cuadrangular (referida a nuestras coordenadas XY, por ejemplo un ángulo de 90 grados), lo que hacemos es cambiar el ángulo mismo, lo que no tiene en este caso sentido.
Pero tal vez, sobre esto tengo todavía que pensar más, desde esa proyección en la que fácilmente podemos dividir el ángulo en tres, se pueda hacer una «contra-proyección» hacia el ángulo primitivo, puesto que las referencias de lo que sería la división ya las tenemos.
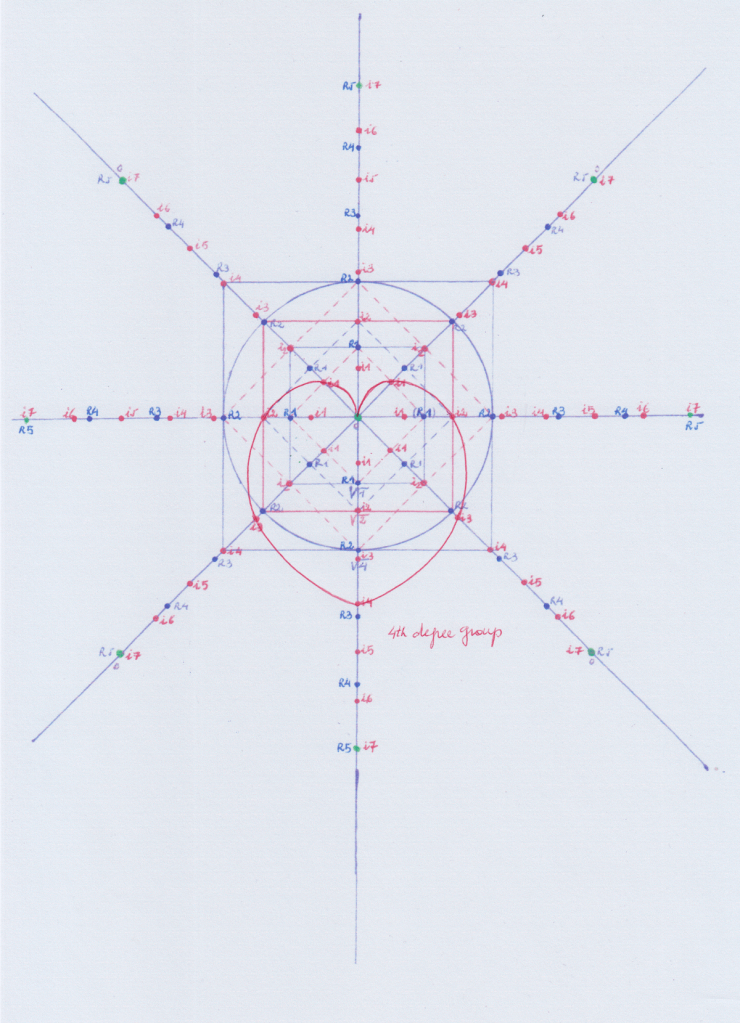
Este sería un ángulo en el que la simetría que tiene permite resolver la trisección sin problema:
Pero no pasaría lo mismo si en vez de en i4, i6, la base estuviera construída en i5 ,i6.
Yo me imagino que tiene que ver gente en matemáticas que esté avanzando en el desarrollo de lo que llaman «geometría visual» y que piense como yo que hay que poner coto a los desmanes que se han cometido con el álgebra en el desarrollo de las matemáticas de los cinco últimos siglos. La situación actual es tan delirante que los matemáticos construyen ecuaciones algebraicas que no saben a qué estructuras materiales corresponden y ni siquiera si es que tienen existencia material alguna. Y cuando les presentas visualmente una estructura de simetría no saben decirte a cual de sus entes algebraicos corresponde. Y si trats de explicárselo con palabras, porque la geometría que les presentas no la reconocen al no ser alegebarica, te piden que les definas los términos.
Es como si alguien que no ha visto nunca la Catedral de Santiago pero que tiene registradas las medidas de la fachada principal, se pusiera a describir con ecuaciones algebraicas el estilo románico del maestro Mateo. Y si tú, con afán de aprender, le preguntas qué son las figuras del arco más alto de la puerta central del Pórtico de la Gloria, te respondiera: «ESO NO ES LENGUAGE MATEMÁTICO ESTANDAR!!!»
(Nota> Los anuncios que pueden salir más abajo la pone la empresa propietaria de la plataforma del blog, ya que este es gratuito aunque la url no lo sea).
—————————————
Actualización 14 septiembre 2021
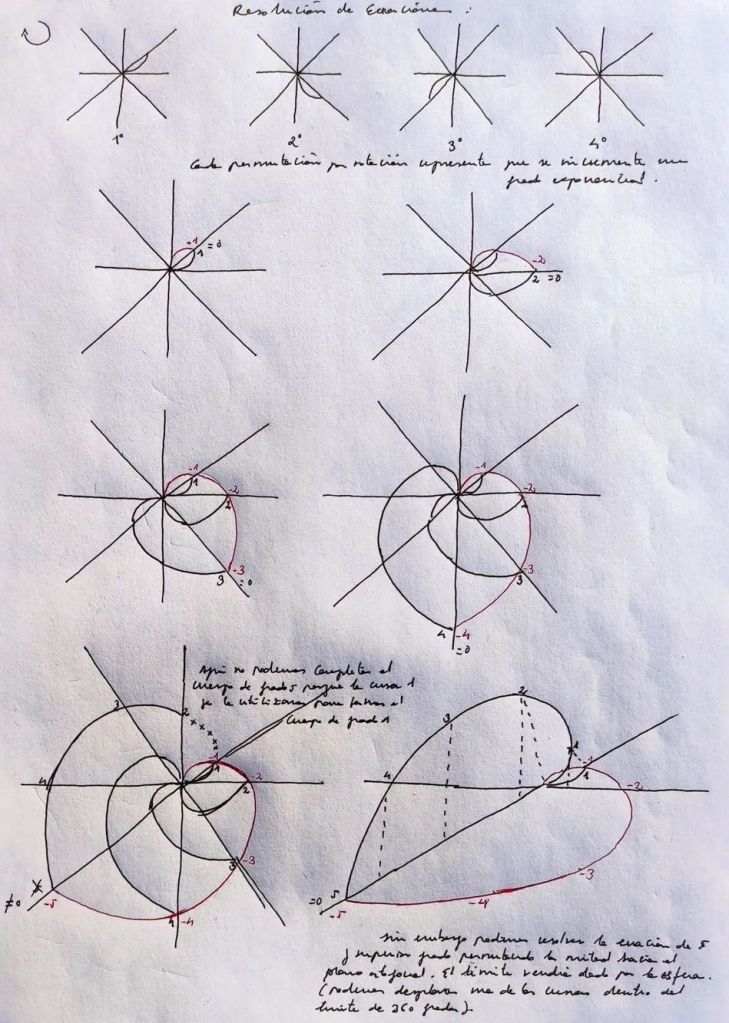
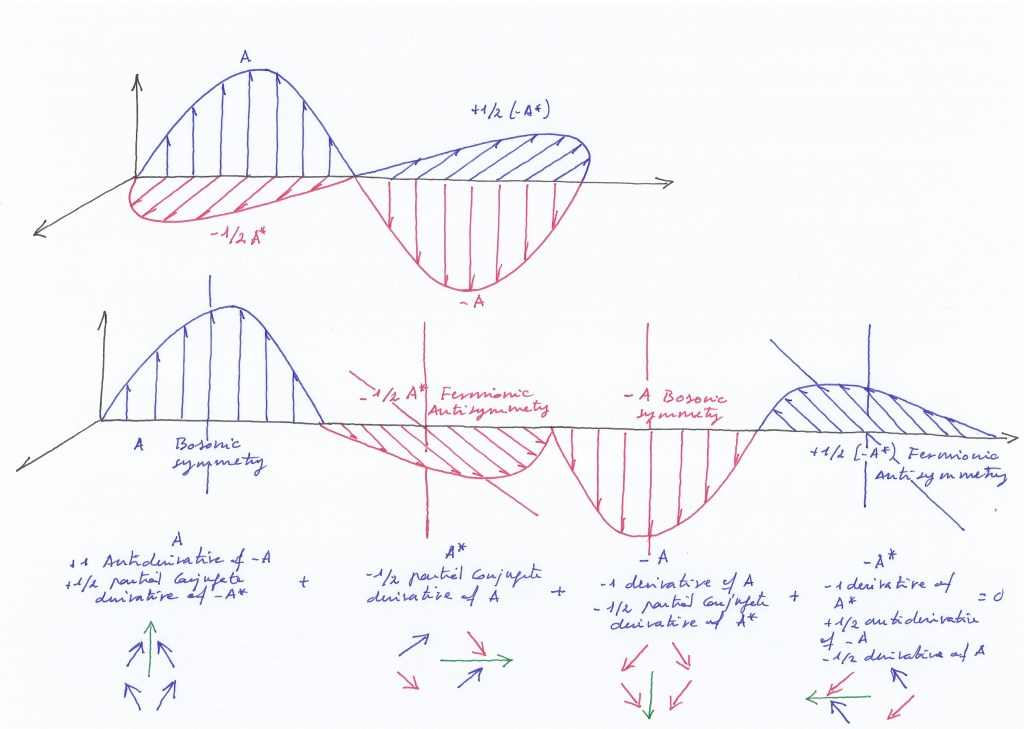
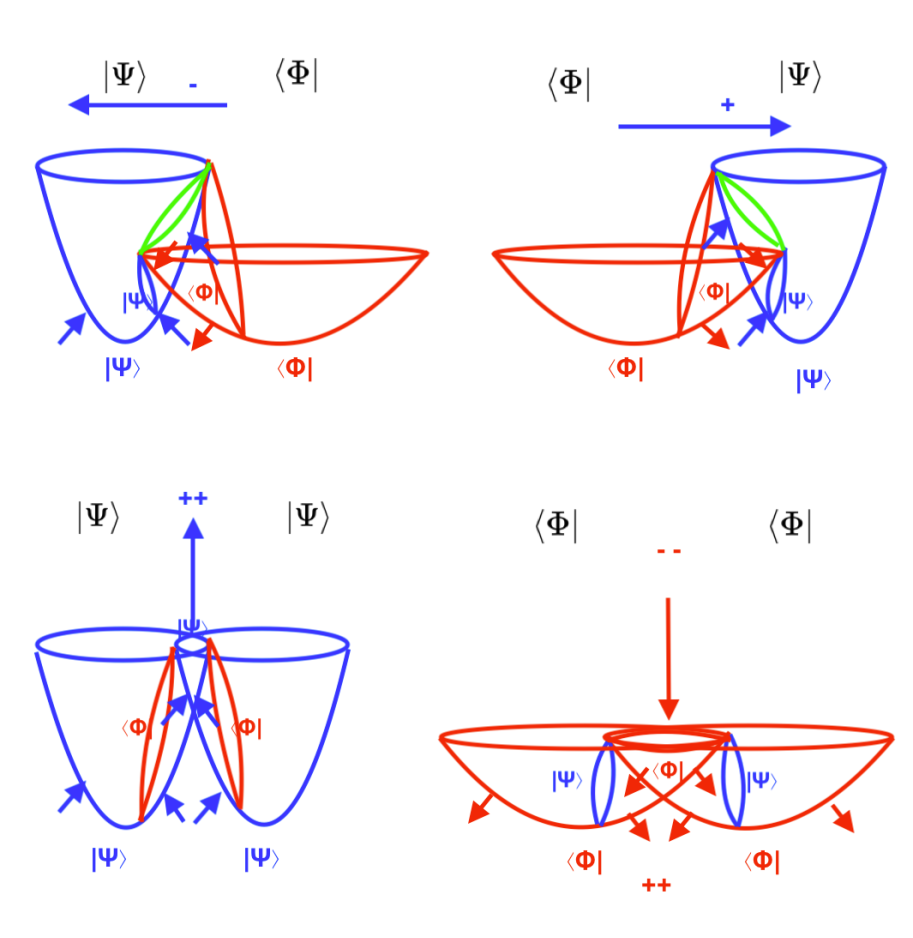
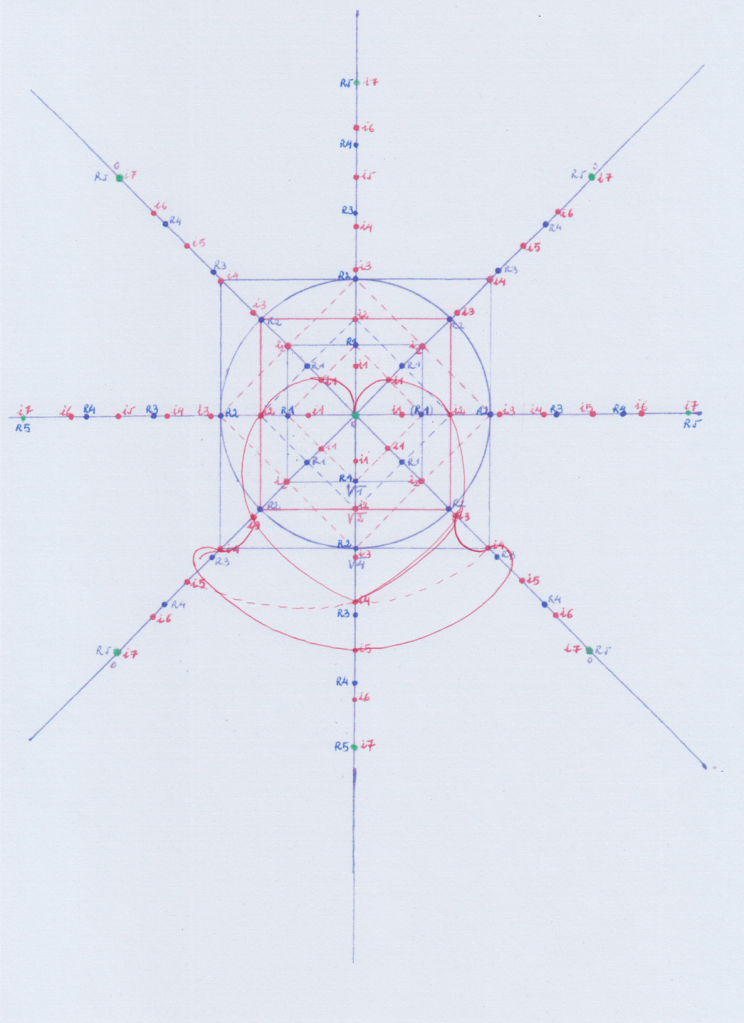
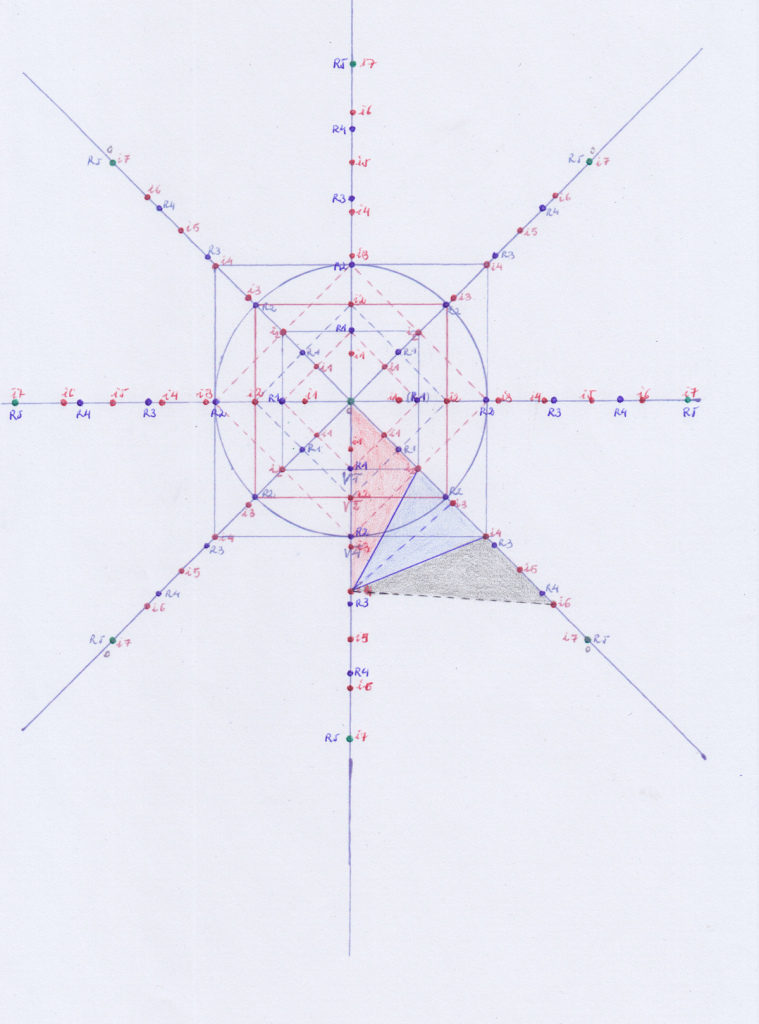
También podemos ver el problema que surge en la resolución de las ecuaciones de quinto y superior grado a través del siguiente gráfico, en el que partimos de una función de grado 1 en la coordenada z, y la vamos rotando a través de las diferentes coordenadas X Y Z. Cada rotación o permutación representa un grado exponencial mayor.
Podemos resolver la función de grado 1 obteniendo un resultado igual a cero si oponemos una función inversa de grado 1, es decir, una función de grado -1. Al enfrentar ambas curvas opuestas además obtenemos un cuerpo delimitado por las dos curvas, que será de grado 1.
Pero cuando llegamos a la quinta permutación nos encontramos con que nos falta el primer tramo, el de grado 1 que nos permita trazar la curva de grados 2, 3, 4 y 5 que se oponga a la curva de grados -1, -2, -3, -4, y -5, ya que la curva +1 de la coordenada Z fue nuestra curva inicial y ya la utilizamos para formar el cuerpo 1.
El problema entonces es como si tuviésemos un edificio de cinco plantas, cada planta tiene una escalera para subir a la planta superior, pero resulta que falta la escalera que va de la planta 1 a la planta dos y por eso no podemos ascender al resto de plantas, aunque las demás sí tengan escalera.
Si el edificio es de seis plantas, nos faltará la escalera de las plantas 1 y 2; si el edificio es de siete plantas, nos faltará la escalera de las plantas 1, 2, y 3. Etc
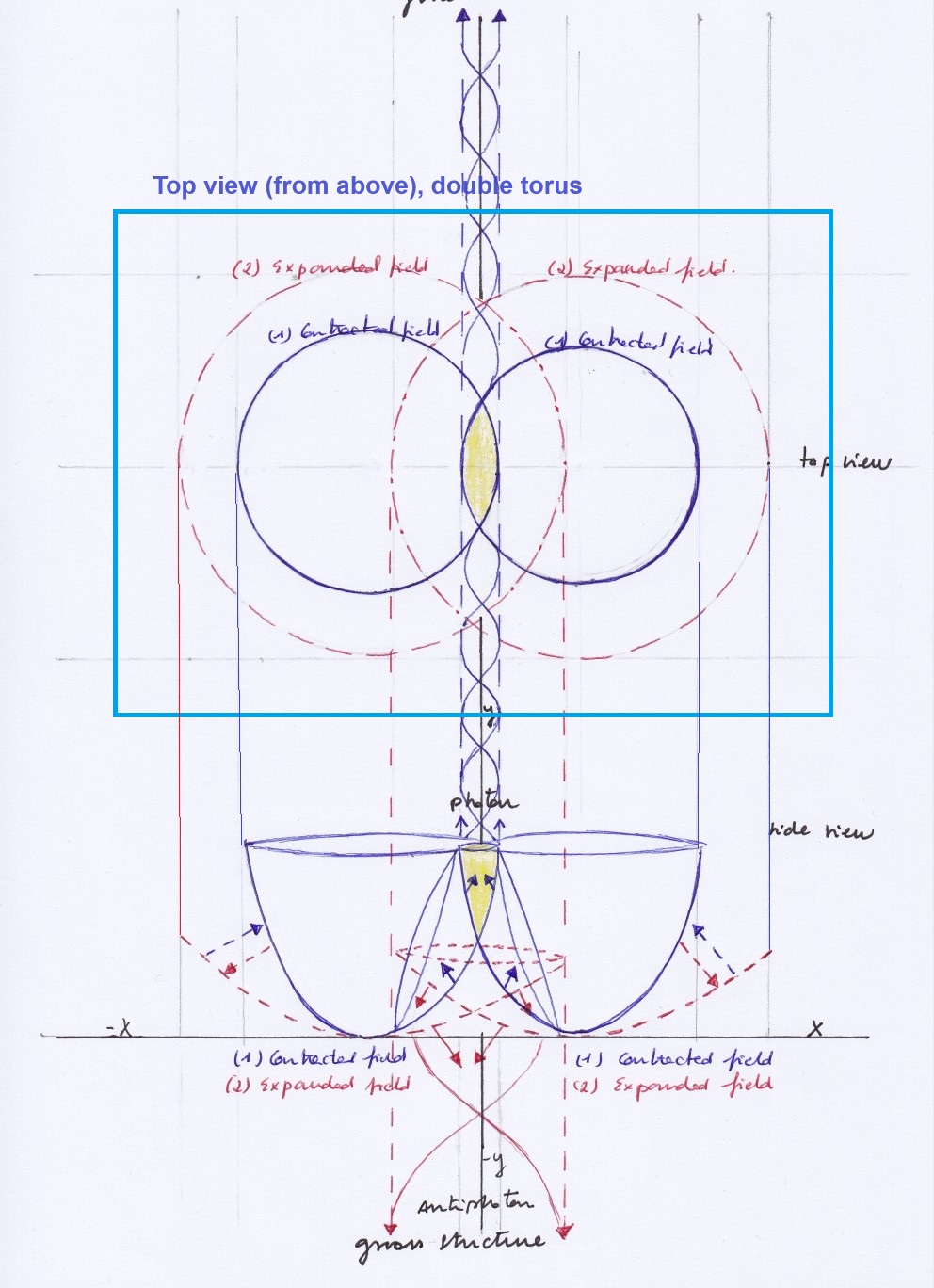
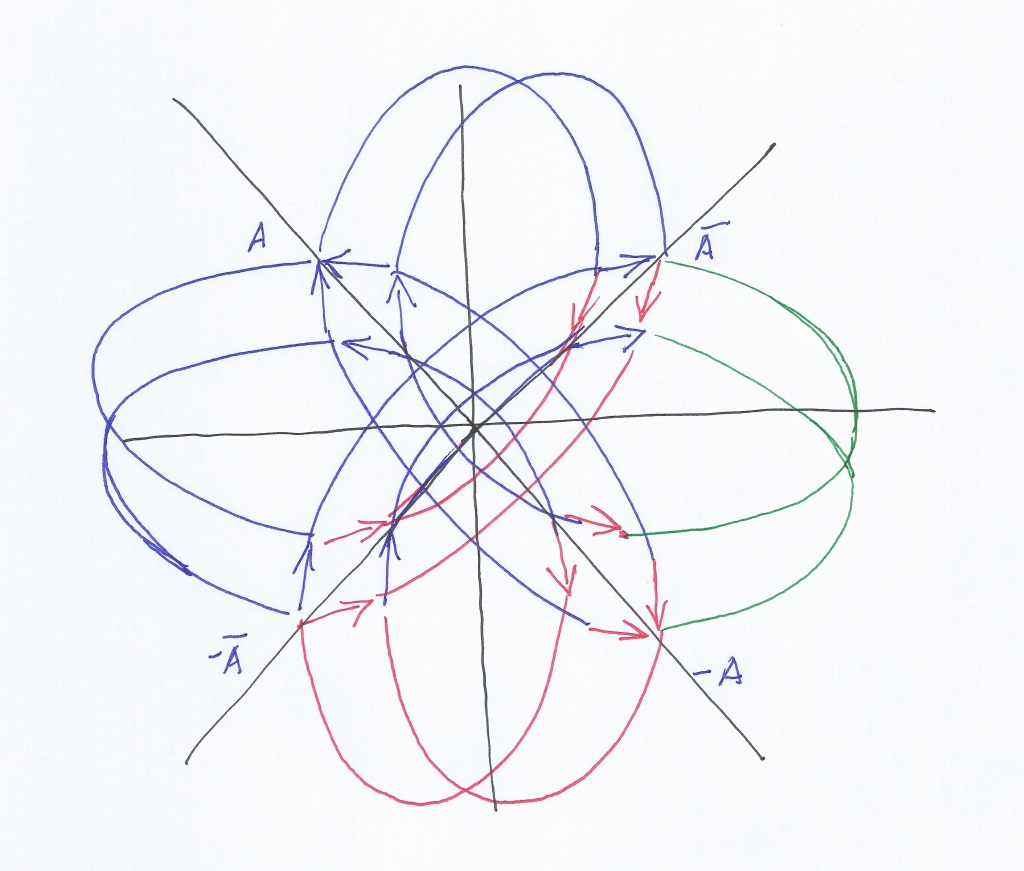
Ahora bien, hasta aquí hemos hecho las permutaciones en un espacio plano. Pero qué ocurre si introducimos una permutación que rote desde el plano horizontal hacia el plano vertical (u ortogonal)? Pues que en este caso sí que vamos a poder resolver las ecuaciones de quinto y superior grado, porque vamos a poder crear nuevas curvas de grado 1, 2, etc para cada ecuación, simplemente rotando el plano sobre el que las construimos.
El límite de las rotaciones en el plano vertical vendrá dado por una esfera. Es decir, no parece que pudiesen resolverse un infinito número de ecuaciones.
Pero cuando hablamos de simetría y asimetría en las ecuaciones de quinto y superior grado en los grupos de Galois, a qué tipo de espacio nos estamos refiriendo? A un espacio plano o a un espacio tridimensional? O es que las ecuaciones algebraicas son algo puramente abstracto descarnado de todo espacio?
Para mí el número, aunque esté representado algebraicamente, no puede existir sin un espacio, porque sin espacio no existe distribución. Y sin distribución no existe número.
Podemos entonces al menos preguntarnos, qué tipo de ecuaciones de quinto y superior grado son aquellas que no pueden resolverse en un espacio bidimensional pero sí en un espacio tridimensional hasta el límite de permutaciones que permite una esfera?
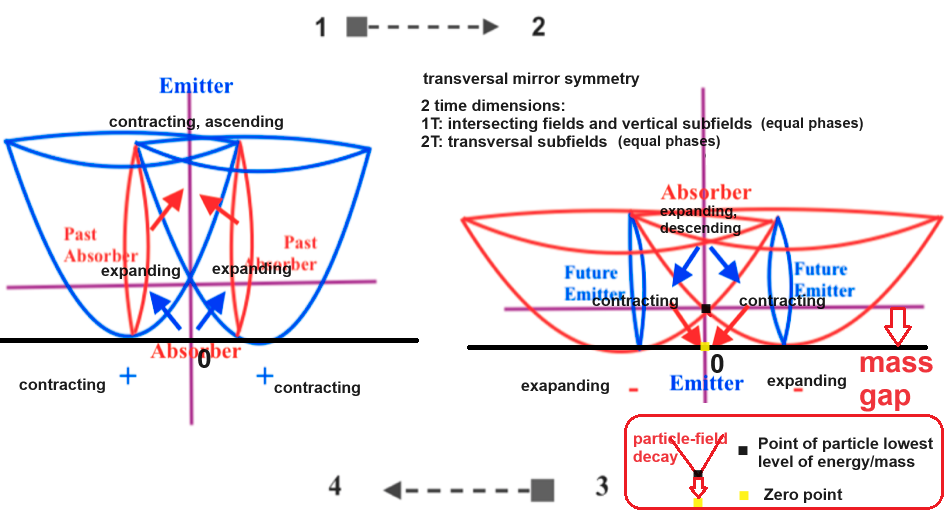
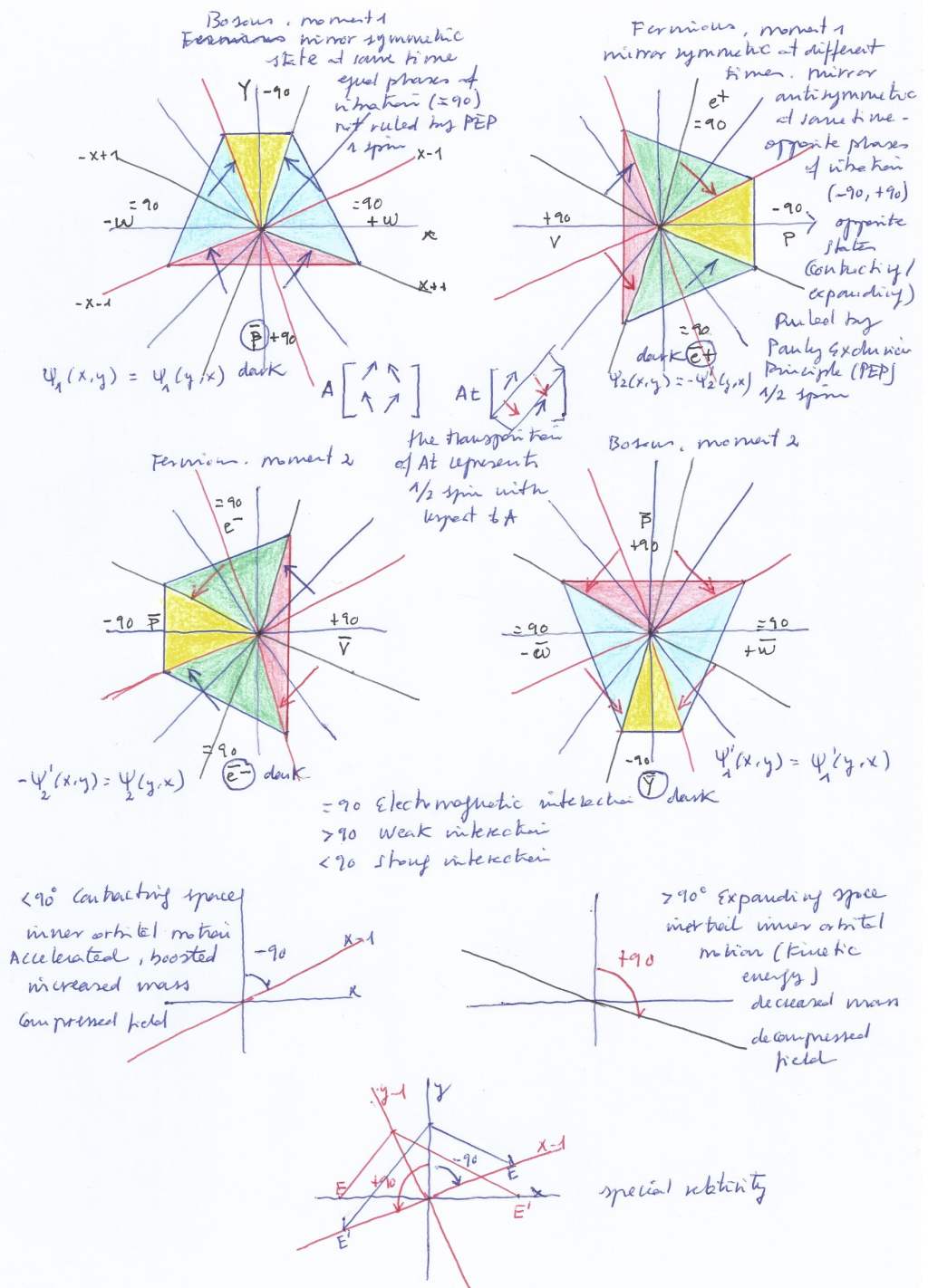
Escribe tu comentario